2.5. ОПТИМИЗАЦИЯ ПО КОМПЛЕКСНЫМ И ВЕКТОРНЫМ КРИТЕРИЯМ КАЧЕСТВА
Как отмечалось в гл. 1, изменение некоторых параметров теплообменных аппаратов весьма существенно сказывается на характеристиках другого оборудования и всей АЭС. В таких случаях при поиске оптимальных параметров целесообразно использовать комплексные критерии качества, учитывающие другие, «сопряженные», характеристики АЭС. Одним из таких критериев может служить стоимость комплекса конденсатор — система охлаждения Ψκ (1-3), при этом основным нелинейным ограничением в процессе поиска является максимально допустимая мощность на прокачку охлаждающей воды Nmax (2.43). Однако Nmax в свою очередь также подлежит оптимизации, особенно для новых схем и типов АЭС, и обычно она определяется на предыдущей стадии разработок, связанной с выбором параметров тепловой схемы и термодинамического цикла АЭС; тогда одним из критериев качества является стоимость установленного киловатта.
Этот же критерий можно применять и для оптимизации «внутренних» параметров комплекса конденсатор — система охлаждения. Его можно представить в следующем виде:
![]() (2.59)
(2.59)
где Ф0 — стоимость оборудования АЭС электрической мощностью Nэ (кроме конденсатора и системы охлаждения), соответствующая расчетным (номинальным) затратам мощности на прокачку охлаждающей воды N0.
Значения Ф0 и N0 принимаются в качестве исходных данных из предыдущей стадии разработок. Величина Ψκ определяется по формуле (1.3), а Фсo — по формуле
![]() (2.60)
(2.60)
где Св — удельные затраты на гидротехнические сооружения, отнесенные к расходу охлаждающей воды;
f(х3, х4) —капитальные затраты на сооружение охладителя, зависящие от расхода охлаждающей воды и ее температуры и определяемые по типовым методам [28, 29].
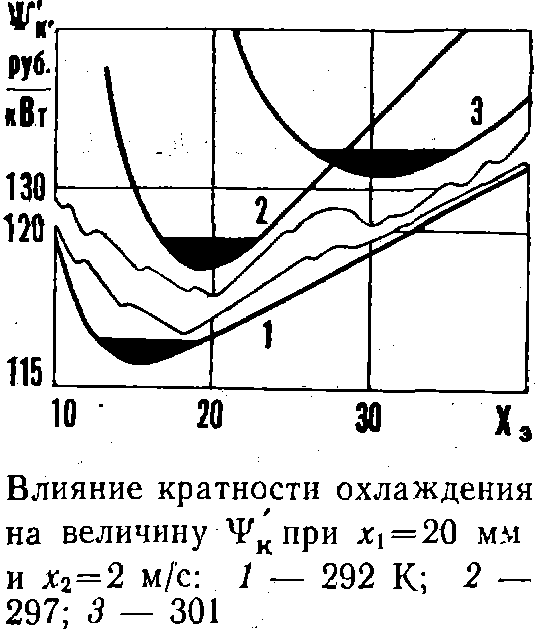
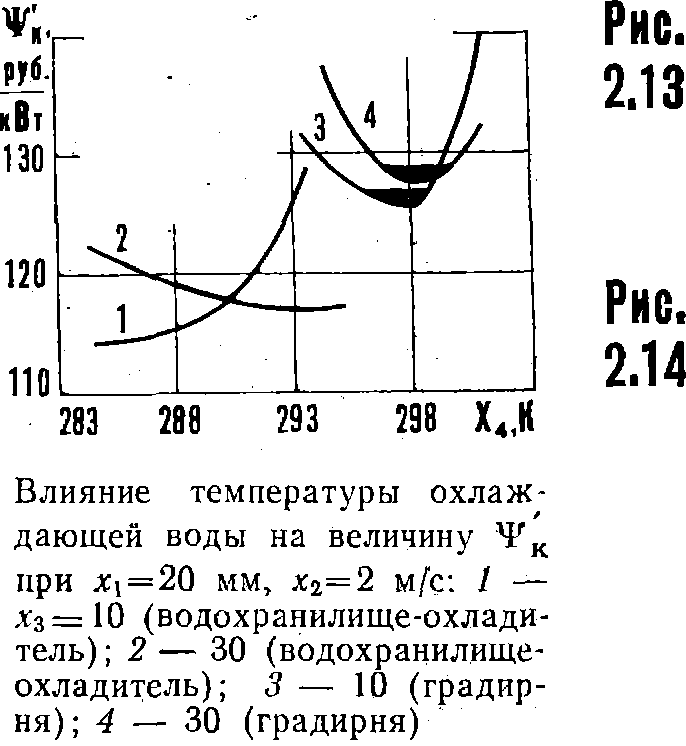
На рис. 2.13 и 2.14 показано влияние кратности охлаждения и температуры охлаждающей воды на величину критерия качества Ψκ при различных значениях других оптимизируемых параметров. Из рисунков следует, что имеют место ясно выраженные экстремумы функции Ψк, численные значения и координаты которых сильно зависят от сочетания других оптимизируемых параметров.
В гл. 1 был сформулирован комплексный критерий качества для оптимизации параметров регенератора АЭС с диссоциирующим теплоносителем Ψρ (см. (1.2)). Величина Ψρ представляет собой сумму стоимости регенератора и эквивалентных капитальных затрат, соответствующих изменению электрической мощности станции ΔΝ вследствие изменения перепада давления по горячей стороне регенератора ΔΡг по сравнению с номинальным уровнем ΔΡго, установленным на предыдущей стадии разработок. В работе [6] показано, что в схемах с промрегенерацией АЭС с диссоциирующим теплоносителем 2.5.

и производится минимизация (или максимизация) критерия Ψ. Но для образования комплексного критерия Ψ необходимо знать так называемые весовые коэффициенты λ. Например, задачу об оптимизации параметров конденсатора по критерию Ψκ можно представить как задачу минимизации двух противоречивых критериев качества: массы конденсатора и площади активной зоны водохранилища-охладителя по скалярному функционалу, где весовыми коэффициентами являются удельная (отнесенная к 1 кг массы) стоимость конденсатора и удельная (отнесенная к 1 м2 активной зоны) стоимость системы охлаждения.
Однако далеко не всегда удается определить и обосновать весовые коэффициенты. К примеру, трудно составить скалярный функционал из критериев М и V для оребренного противоточного теплообменника или теплообменника с воздушным охлаждением. Существует принципиально иной подход к поставленной проблеме — векторная оптимизация, который применяется в настоящее время для широкого круга задач оптимального управления (программирование оптимальных траекторий, аналитического конструирования оптимальных регуляторов, исследования операций и др.). Сущность метода заключается в определении идеальной (утопической) точки, координатами которой являются экстремальные значения каждого в отдельности критерия качества, и в нахождении реальной точки в пространстве оптимизируемых параметров, характеризующейся наибольшей близостью критериев качества к своим наилучшим значениям. Описание и обоснование этого метода приводятся в гл. 4.

