Изложенные выше методы, как детерминированные, так и случайные, являются, по существу, локальными, т. е. они обеспечивают (с заданной точностью) попадание в точку локального экстремума, в зоне притяжения которого находится начальная точка поиска Х(0). В то же время, как показывает анализ, критерии качества при оптимизации параметров теплообменных аппаратов могут быть многоэкстремальными функциями оптимизируемых параметров. Таким образом, для решения поставленной задачи необходим метод, который позволял бы находить глобальный экстремум функции качества.
Предлагаемые в литературе способы [32, 58], основанные на сочетании метода сканирования (с большим шагом) с последующими локальными поисками вершин, по существу, сводятся к перебору локальных экстремумов и запоминанию наибольшего или наименьшего из них. Значительно более эффективным является так называемый метод Ψ-преобразования, разработанный В. К. Чичинадзе [59].
Сущность метода заключается в преобразовании оптимизируемой функции с помощью равномерно распределенной случайной выборки точек в многомерном пространстве параметров в монотонно убывающую одномерную функцию, нулевое значение которой соответствует величине глобального экстремума. Такой подход позволяет с достаточной точностью предсказать значение функции в глобальной точке и с приемлемой вероятностью выделить область притяжения глобального экстремума.
ОПРЕДЕЛЕНИЕ ПРИБЛИЖЕННОГО ЗНАЧЕНИЯ ФУНКЦИИ В ГЛОБАЛЬНОЙ ТОЧКЕ МЕТОДОМ Ψ-ПРЕОБРАЗОВАНИЯ
Поиск по данному методу состоит из трех этапов. На первом этапе вычисляются значения минимизируемой функции качества в N точках, выбранных случайным образом, по полученным результатам строится монотонно убывающая функция Ψ (ζ), где ζ — скаляр, т. е. значение функции Q при фиксированных значениях оптимизируемых параметров (независимых переменных) xit Х2, ..., Хп- Функция Ψ(ζ) определяется следующим образом: 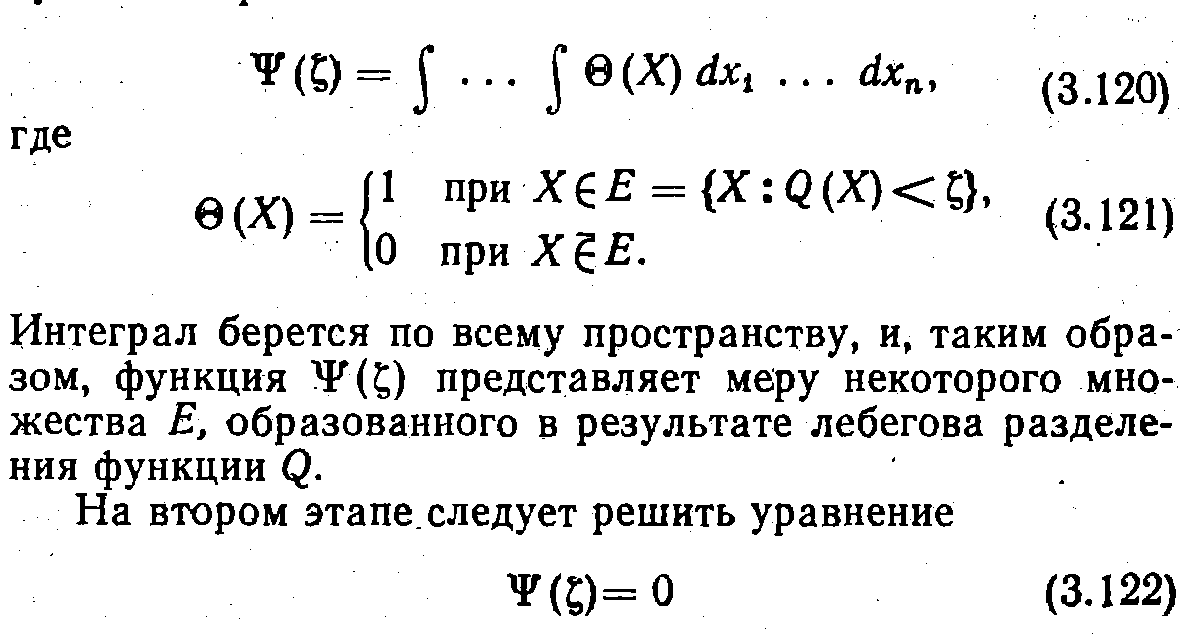
и определить величину глобального экстремума.
Третий этап включает в себя определение параметров, соответствующих значению глобального экстремума. Из наиболее близкой к глобальному экстремуму точки происходит движение к цели по известным локальным методам.
Программа поиска глобального экстремума для функций типа (3.1) была реализована на ЭЦВМ "БЭСМ-4" [60]. Блок-схема программы представлена на рис. 3.6, геометрическая интерпретация метода — на рис. 3.7. Вначале задаемся числом и значениями уровней ζk(k=l, 2, ..., l), соответствующих некоторым дискретным значениям функции Q.
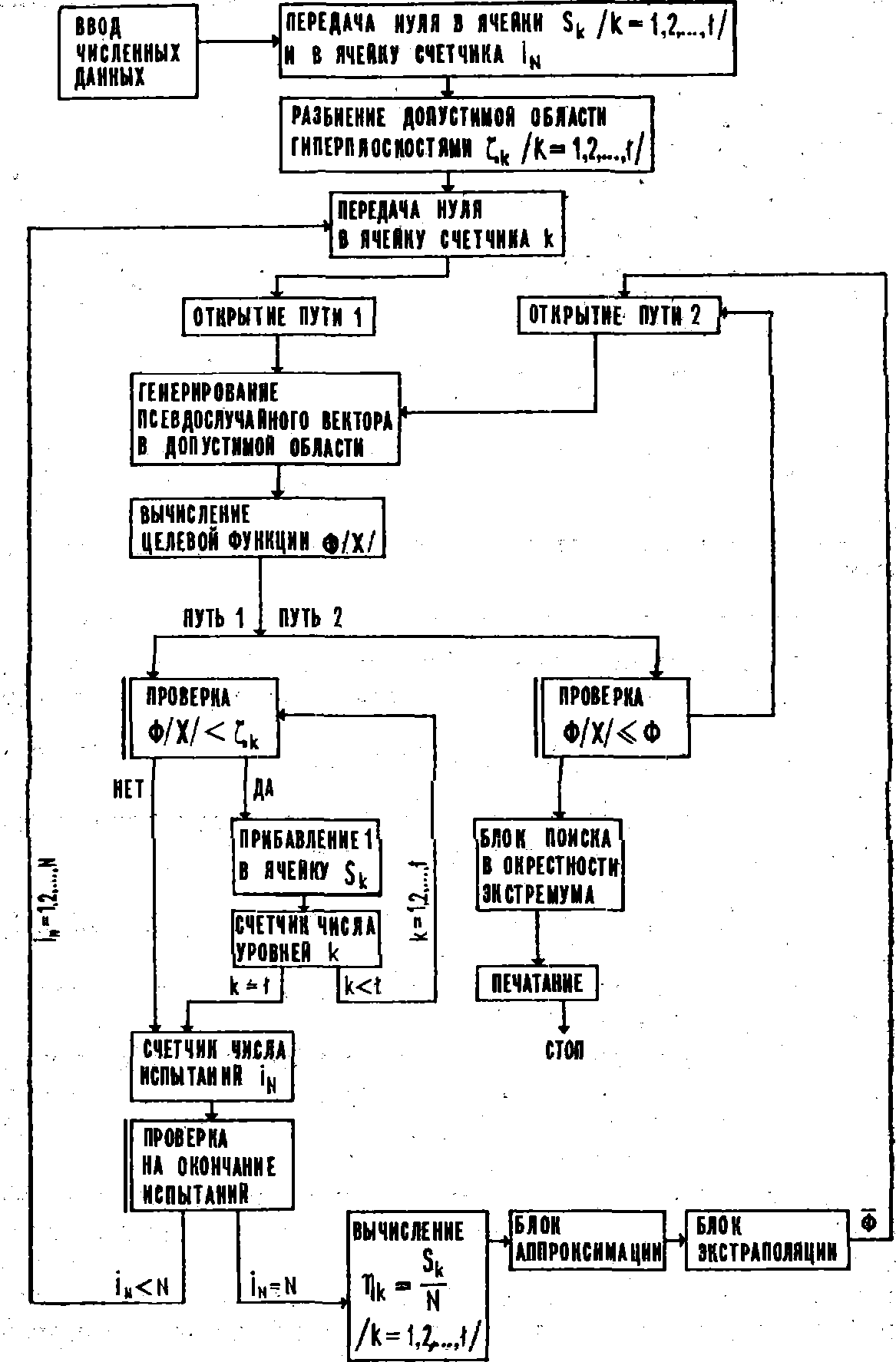
Блок-схема программы поиска глобального экстремума методом Ψ-преобразования
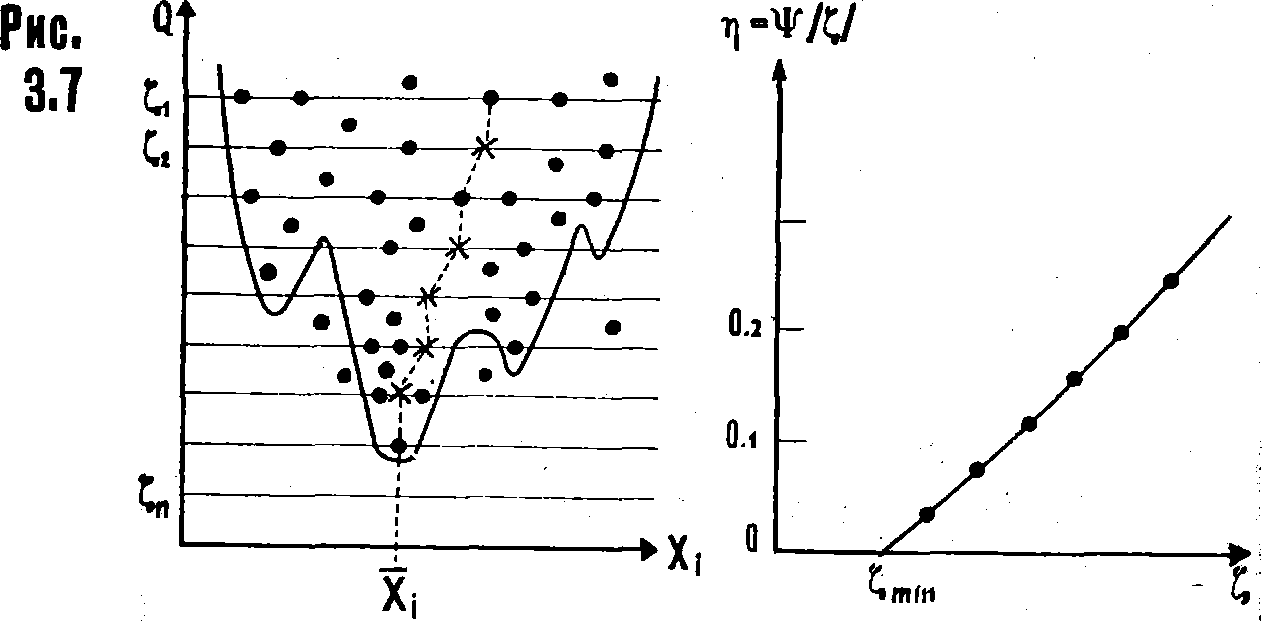
Геометрическая интерпретация метода поиска глобального экстремума
Посредством специальной подпрограммы в допустимой области получаем псевдослучайные точки, подчиненные равномерному распределению, и вы числяем значение целевой функции (3.1) в этих точках. На основе указанных вычислений определяем величину
![]() (3.123)
(3.123)
которая представляет относительную частоту попадания случайной допустимой точки в область
![]() (3.124)
(3.124)
Для практического использования программ достаточно ограничиться l=10 и N=1000.
Посредством аппроксимации реализованных точек получаем аналитическую зависимость η=Ψ(ζ). Корень этого уравнения соответствует значению целевой функции в глобальной точке.
Описанная выше процедура позволяет получить ожидаемое значение глобального минимума функции качества, но еще не решает поставленной задачи — определение координат глобального экстремума, т. е. оптимальной комбинации параметров теплообменных аппаратов.
ОПРЕДЕЛЕНИЕ КООРДИНАТ ГЛОБАЛЬНОГО ЭКСТРЕМУМА
Приближенный метод определения координат глобального экстремума основывается на предположении о том, что координаты центра тяжести множеств Ek (3.124), образованных в результате лебегова разделения оптимизируемой функции Q(X), сводятся к координатам точки экстремума при![]() .
.
Доказательство этого предположения дано в работе Н. И. Джибладзе [61].
Алгоритм вычисления центров тяжести множеств (3.124) укладывается в схему статистических испытаний, используемую в методе Ψ-преобразования для определения меры множеств Ek. Так как математическое ожидание случайной величины X связано со средним арифметическим выборочных значений случайной величины при большом числе испытаний и, согласно закону больших чисел,

(3.125)
3.4.

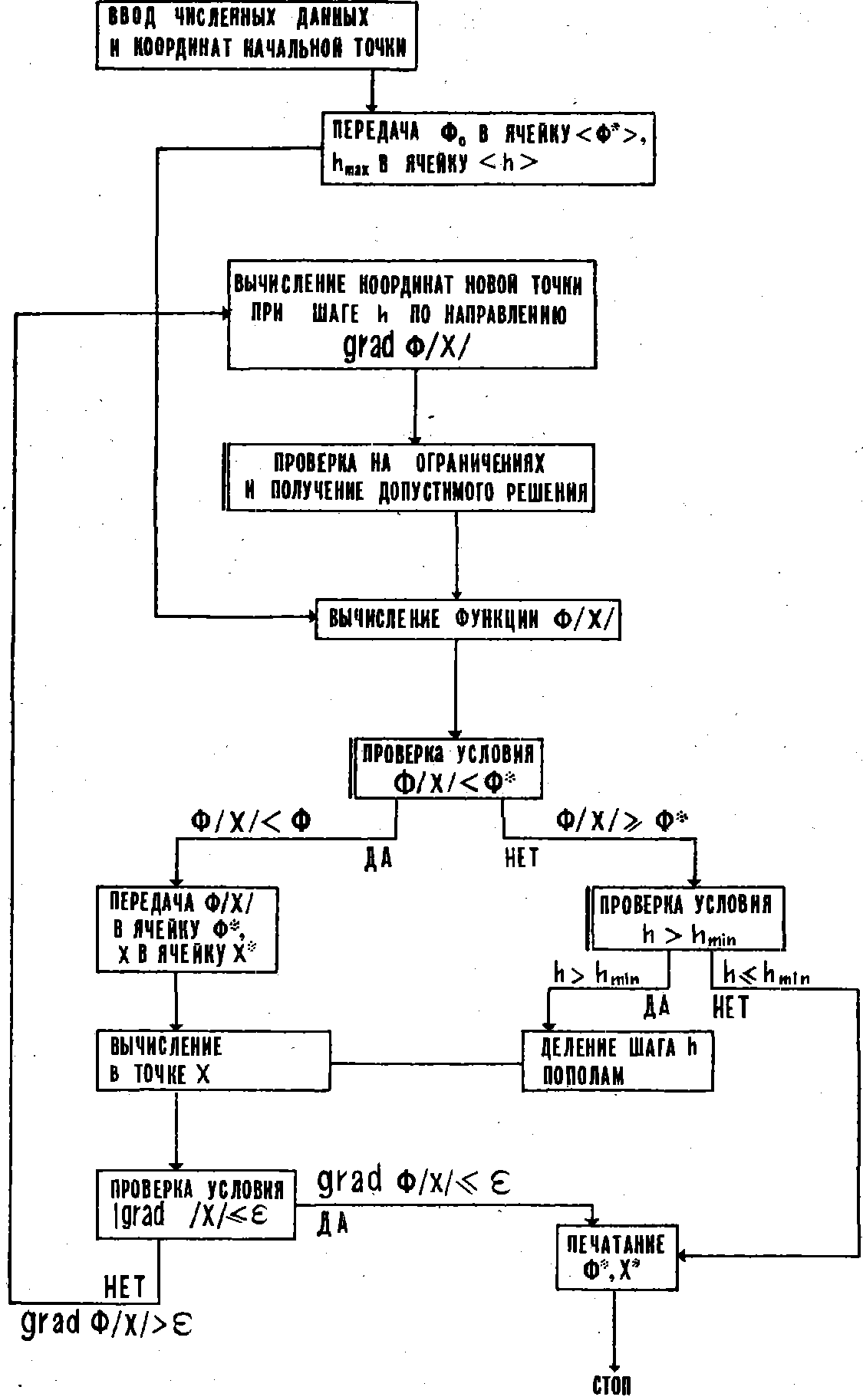
Рис 3.8. Блок-схема поиска локального экстремума

Алгоритм поиска методом градиента с пропорциональным шагом имеет почти ту же схему, за исключением того что новое приближение определяется по выражению
![]()

