Характеристикой любой случайной величины является функция распределения этой величины. При этом для оценки показателей надежности не восстанавливаемых объектов по данным об отказах могут использоваться либо экспериментальное распределение наработки до отказа, либо теоретическое распределение. Чаще при вероятностных методах исследования надежности используются теоретические распределения. В данной главе рассматриваются теоретические законы распределения случайных величин.
При этом формы записи этих законов могут быть различными. Для непрерывных случайных величин в основном используется интегральная форма записи F(t) и две дифференциальные: плотность распределения случайной величины f(t) и условная плотность распределения λ(ί).
Для положительных случайных величин в теории и практике надежности часто применяются следующие типы законов распределения:
- для непрерывных случайных величин - экспоненциальный, нормальный, логарифмически нормальный, Вейбулла, гамма-распределения и др.;
- для дискретных случайных величин - биноминальный н редких событий (Пуассона).
Законы распределения имеют следующие особенности:
- зависят от вида и характера отказов;
- зависят от периода жизни объекта (период проектирования, изготовления, эксплуатации);
- каждый закон имеет определенную характеристику распределения и соответствующую ей функцию, вид расчетных формул, которые даются в справочных пособиях.
При использовании законов распределения в расчетах надежности числовые значения случайных величин (например, показателей надежности) могут иметь либо точечную (однозначную) оценку, либо приближенную оценку с доверительными границами интервалов, которые с заданной доверительной вероятностью покрывают все возможные значения показателей надежности. В расчетах непрерывных случайных величин чаще всего применяются экспоненциальный и нормальный законы.
Эти законы рассмотрим более детально, а по остальным, которые назовем условно дополнительными (промежуточными), дадим некоторые особенности.
Законы распределения непрерывных случайных величин
Экспоненциальный закон. Этот закон широко используется применительно к отказам, возникающим внезапно и вызванным случайными внешними воздействиями: ростом тепловых, механических, электрических нагрузок или ошибками проектирования, изготовления и эксплуатации. Часто экспоненциальный закон используют в начале эксплуатации (период приработки), и предпочтение отдается сложным техническим системам с большим числом элементов. Он характеризуется относительной простотой и приемлемой точностью получаемых результатов (а иногда и в запас). Это однопараметрический и единственный закон распределения случайной величины с условной плотностью λ(t) = λ - const, который является параметром экспоненциального закона. Основные характеристики экспоненциального закона даны в табл. 6.
Таблица 6

Графическое представление характеристик экспоненциального закона дано на рис. 9.
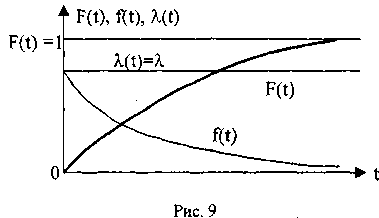
На рис. 9 показано, что кривая распределения плотности случайной величины f(t) показательна по отношению к функции надежности (1- F(t)). Поэтому этот закон называют еще и показательным, то есть время работы
до отказа в рассматриваемом случае распределено показательно с параметром λ(ί) = λ.
Нормальный закон. Этот закон хорошо описывает постепенные, медленно накапливающиеся отказы и является предельным, так как к нему приближаются другие законы распределения (гамма-распределения, биноминальный и др.). В расчетах надежности нормальный закон применяется при рассмотрении отказов, вызванных коррозией, старением, постепенным износом. Нормальный закон применяется и при анализе надежности сложных систем с учетом превышения предельных параметров. Характеристики нормального закона даны в табл. 7.
Таблица 7

В табл. 7 в целях упрощения расчетов соответствующих функций вместо математических зависимостей использованы табулированная функция Лапласа и функция плотности нормального распределения случайной величины.
Функция Лапласа![]()
где t - время, для которого определятся функция;
Tср - математическое ожидание;
σ - среднее квадратичное отклонение параметра нормального закона.
Графическая иллюстрация характеристик нормального закона, усеченного на интервале (0, ∞), представлена на рис. 10.
Особенности дополнительных (промежуточных) законов распределения случайных величин.

Усеченный нормальный закон распределения. Учитывая, что использование нормального закона в расчетах надежности ограничивается определенными условиями (математическое ожидание M[t] должно быть больше 0 и больше 3σ), закон можно считать действующим при t > 0. В противном случае используется усеченный осью ординат (то есть с отброшенной отрицательной частью) нормальный закон.
При этом численные значения параметров усеченного нормального закона и нормального остаются одинаковыми. Расчетные аналитические выражения даются в учебных пособиях и справочниках по расчету надежности.
Закон Вейбулла. Закон Вейбулла описывает широкий спектр распределения случайных величин и поэтому часто используется в расчетах надежности.
Он хорошо описывает распределения, связанные со старением конструкционных материалов и с временем безотказной работы системы, состоящей из большого числа последовательно соединенных элементов. В зависимости от величины параметра к формы закона Вейбулла могут меняться. При k = 1 распределение Вейбулла становится тождественным экспоненциальному распределению. При k > 1 условная плотность λ(ί) возрастает, а при к < 1 - убывает. Аналитическая зависимость и характер изменения во времени основной характеристики даны в табл. 8.
Логарифмически нормальный закон. В этом законе принимается нормальное распределение не самой случайной величины, а ее логарифма. В соответствующих аналитических выражениях вместо случайной величины подставляется логарифм этой случайной величины. Этот закон часто используют при обработке экспериментальных и эксплуатационных данных; например, при усталостной прочности и коррозионном разрушении. Следует отметить, что характерной особенностью у всех трех нормальных законов функция условной плотности распределения возрастающая.
Закон гамма-распределения. Этот закон является так же, как и закон Вейбулла, универсальным, так как имеет многообразные формы распределения, связанные с описанием мгновенных отказов, которым предшествует постепенное накопление элементарных неисправностей и повреждений за счет ухудшения прочностных и усталостных свойств материалов. Рассматриваемое распределение хорошо относится к периоду установившегося износа и особенно к отказам, связанным с механическим износом. Применяется закон также на начальной стадии эксплуатации, если параметр гамма-закона к < 1 и отказы возникают при приработке объекта. Параметр к характеризует асимметрию гамма-распределения.
В зависимости от величины к изменяется вид основных характеристик. Так, при к = 1 гамма- распределение переходит в экспоненциальное распределение, а при к > 1 - в нормальное. Аналитические зависимости основных характеристик гамма-распределения даны в табл. 8.
Таблица 8

Законы распределения дискретных случайных величин
Для дискретных случайных величин чаще всего применяют биномиальный закон распределения и закон редких событий или Пуассона.
Биномиальный закон распределения. При исследовании надежности сложных систем часто приходиться встречаться со случаями, когда происходят независимые отказы. Для таких отказов применима теорема теории вероятностей о повторении опытов, которая позволяет вывести формулу, представляющую собой распределение вероятностей по различным исходам дискретной случайной величины. Это распределение называется биномиальным. К нему приводит следующая часто встречающаяся на практике математическая модель.
Пусть система состоит из η независимых однотипных элементов (подсистем), участвующих в опыте, а вероятность появления отказов - m. При этом каждый элемент может отказать с вероятностью q(t) либо отработать безотказно установленное время с вероятностью P(t). В этих условиях вероятность того, что из η элементов системы m элементов окажутся в состоянии отказа, выражается формулой Бернулли
![]() (33)
(33)
где ...
![]()
η и q - параметры биноминального закона;
![]() - число сочетаний m элементов из п.
- число сочетаний m элементов из п.
Для случая, когда необходимо определять вероятность того, что из η элементов системы к элементов отработают безотказно установленное время, формула Бернулли имеет вид
![]() (34)
(34)
Математическое ожидание для биномиального распределения как среднее число появления рассматриваемого события равно:
- для отказа mcp = M[m] = n q;
- для безотказной работы кср = М[к] = η р,
где m и к- соответственно число отказавших или безотказно проработавших элементов, a q и р - вероятности отказа и безотказной работы одного элемента.
В этом случае дисперсия определяется следующей формулой:
![]() (35)
(35)
В общем случае, если вероятность того, что случайная величина m примет значение в интервале 0 < m < n, то уравнение биноминального распределения будет иметь вид
![]() (36)
(36)
Основные свойства биноминального распределения:
При η →∞ биноминальный закон стремится к нормальному с параметрами:![]()
При n→∞ и q→0 и nq=const, биноминальный закон переходит в распределение Пуассона.
Графическая иллюстрация биноминального закона распределения представлена на рис. 11.
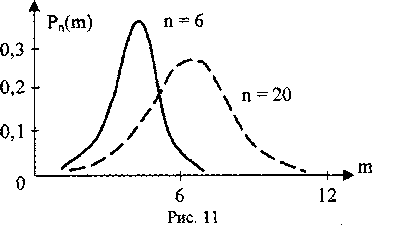
Закон Пуассона. Закон Пуассона основан на идентичной математической модели, что и биномиальный закон, но при малых значениях вероятности возникновения событий (отказов) q < 0,1 и большом числе испытываемых элементов η > 10. Поэтому его называют законом редких событий и он является частным случаем закона биноминального распределения.
Однако закон Пуассона применяется в более широком понимании случайных событий. В этом законе рассматриваются не только m событий в η опытах, а случайные события и другого вида за некоторый произвольный расчетный интервал, если известно среднее число данных событий на единицу рассматриваемого интервала. В качестве интервалов могут рассматриваться интервалы:
- времени -1;
- пространства (поверхности или объема) - S, V;
- расстояния - L и другие.
В качестве среднего числа событий на единицу интервала могут приниматься, например, среднее число отказов элемента за заданное время или среднее число дефектов (микротрещин) на единицу поверхности оболочки ТВЭЛ.
Закон Пуассона характеризует вероятность того, что на исследуемом расчетном интервале рассматриваемое событие произойдет (возникнет) m раз. Расчетная формула для этого закона имеет вид, если в качестве случайной величины принято число отказов m за интервал времени (0, t), где λ - интенсивность отказов;
λt = а - параметр закона.
Вероятность того, что случайная величина m, распределенная по закону Пуассона, примет значение в интервале m1< m < m2, вычисляется по формуле
![]()
(38)
при значении параметра а > 0 закон Пуассона приближается к нормальному закону с параметрами М[т] = а, и σ = √a .
Графическая иллюстрация закона Пуассона представлена на рис. 12.

Рис. 12

