Глава 3
ФУНКЦИОНАЛЬНЫЕ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Функциональные характеристики случайных величин
Для количественной оценки надежности оборудования АЭС используется целый ряд показателей надежности, которые количественно характеризуют безотказность, долговечность, ремонтопригодность и сохраняемость этого оборудования. Характерной особенностью показателей надежности является то, что они представляют собой функциональные и числовые характеристики случайных величин и определяются как вероятностные характеристики на основе методов теории вероятности и математической статистики. Например, среднее время безотказной работы или наработка до отказа, число отказов за время t или срок службы - календарное время эксплуатации объекта до предельного состояния.
В теории надежности случайная величина используется для количественной оценки случайных событий - отказов в работе элементов АЭС.
Случайные величины могут быть непрерывными, то есть могут принимать любые значения в некотором непрерывном промежутке времени (t1< t < t2) или дискретными, то есть могут принимать отдельные дискретные значения (t = t1; t = t2...).
Для определения случайных величин необходимо знать их возможные значения и вероятности их появления, то есть зависимости между возможными значениями случайных величин и вероятностями их появления. При наличии статистических данных случайных величин можно для них построить законы распределения. На основе этих законов можно определять все необходимые показатели надежности.
Универсальной формой закона распределения любой случайной величины (непрерывней и дискретной) является интегральный закон распределения, или функция распределения этой случайной величины, которую будем обозначать F(t).
К основным законам распределения случайных величин относятся функциональные характеристики случайных величин:
- функция распределения - F(t);
- функция плотности распределения - f(t);
- функция условной плотности распределения - X(t), а также числовые характеристики случайных величин:
- среднее значение случайной величины - Тср;
- дисперсия - Д(t);
- среднее квадратичное отклонение среднего значения случайной величины - σ;
- гамма-процентное значение случайной величины Τγ.
Функция распределения случайной величины
Функциональная характеристика F(t) численно равна вероятности случайного события (отказа) и определяется как вероятность того, что случайная величина τ (например, наработка до отказа) будет меньше заданной наработки t:
![]() (11)
(11)
Физически это означает, что функция F(t) является функцией ненадежности, так как показывает, что фактическое время наработки до отказа τ меньше заданного времени t.
Функция F(t) обладает следующими свойствами: при t = ∞ P(t = ∞) = 1; при t = 0 P(t = 0) = 0.
Для непрерывных случайных величин функция F(t) - возрастающая непрерывная (рис. 4), а для дискретных - ступенчатая возрастающая функция (рис. 5).
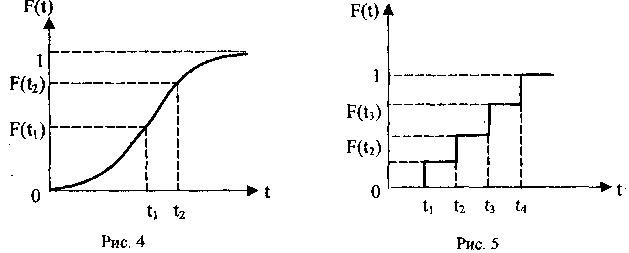
Рассмотрим графики, представленные на рис. 4 и 5.
Для рис. 4 можно записать, используя теорему сложения вероятностей,
![]() (12) или
(12) или
![]() (13)
(13)
Следовательно, вероятность попадания случайной величины в интервалах времени t1< t < t2 равна разности значений ее функции распределения в конечной и начальной точках интервала.
Для рис. 5 имеем для дискретной случайной величины
![]() (14) или
(14) или
![]() (15)
(15)
Из уравнений и рис. 5 следует, что высота отдельной ступеньки функции распределения F(t) дискретной случайной величины равна вероятности Р, того, что случайная величина примет дискретное значение ti, отвечающее этой ступеньке:
![]() (16)
(16)
Вероятности рi образуют ряд распределения дискретной случайной величины. Уравнение (5) является общим для непрерывных и дискретных случайных величин и поэтому интегральная форма закона F(t) является универсальной.
Функция плотности распределения случайной величины
Для описания непрерывной случайной величины в бесконечно малом интервале времени, кроме интегральной функции F(t), используется дифференциальная функция случайной величины, то есть производная функция от интегрального закона распределения случайной величины, которая называется плотностью распределения или дифференциальным законом распределения случайной величины и обозначается f(t):
![]() (17)
(17)
По физическому смыслу f(t) есть вероятность того, что случайная величина τ примет некоторое значение в малом единичном интервале (t + dt) около заданного t:
![]() (18)
(18)
Таким образом, f(t) представляет собой вероятность попадания случайной величины τ в очень малый интервал около заданного t.
Основные свойства этой функции:
f(t) - неотрицательная функция;
f(t > 0) > 0, f(t = ∞) = 0.
Между F(t) и f(t) существует соответствие
![]() (19)
(19)
Величина f(t)dt характеризует появление отказа за интервал времени (t, t + dt). Графическое изображение функции f(t) дано на рис. 6.
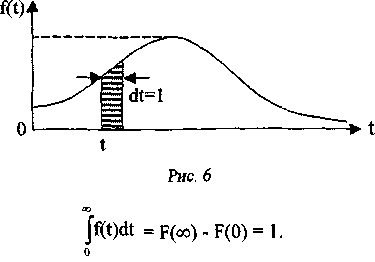
Площадь под кривой f(t) равна единице.
Следует отметить, что использование f(t) как показателя надежности не всегда удобно, так как эта функция не показывает, был ли отказ объекта до заданного времени t или нет. В целях устранения указанного условия вводится дополнительная функция условной плотности распределения случайной величины.
Функция условной плотности случайной величины
Кроме F(t) и f(t) для описания непрерывной случайной величины применяется еще один дифференциальный закон распределения непрерывной случайной величины - условная плотность или условный дифференциальный закон распределения случайной величины k(t).
По физическому смыслу условная плотность - это условная вероятность того, что случайная величина τ примет значение в бесконечно малом единичном интервале около точки t [t, t + (dt =1)] при условии, что до этого момента значение τ не реализовывалось (не было отказа, т.е. τ > t):
![]() (21)
(21)
Иначе Z(t) - условная плотность вероятности возникновения отказа объекта для заданного t при условии, что до этого момента времени t отказ не возникал.
Для не восстанавливаемых после отказа объектов условную плотность распределения случайной величины (условную вероятность отказа) за время t также называют интенсивностью случайной величины (интенсивностью отказа), а для восстанавливаемых объектов в качестве условной плотности распределения случайной величины (условной плотности отказов) применяется понятие параметра потока отказов.
Интенсивность отказов обозначается обычно λ(1), а параметр потока отказов - w(t). Графическое изображение возрастающей функции X(t) дано на рис. 7.

В табл. 5 даны соотношения между тремя функциональными характеристиками распределения непрерывной случайной величины.
Таблица 5


