В качестве основных числовых характеристик случайных величин применяются:
- среднее значение случайной величины Тср;
- дисперсия случайной величины Д (t);
- среднее квадратичное отклонение случайной величины σ;
- гамма-процентное значение случайной величины Τγ.
Среднее значение случайной величины Тср. Среднее значение случайной величины Тср или математическое ожидание случайной величины является основной числовой характеристикой случайной величины. Оно определяется как среднее арифметическое от опытных выборных значений рассматриваемой случайной величины.
Например, для η наработок t, на отказ
(22)
Теоретическая формула для Тср непрерывной случайной величины τ имеет вид
(23)
Для дискретной случайной величины по определению Тср имеет вид
(24) где р; - ряд распределения вероятностей дискретной случайной величины, имеющей к возможных значений.
Дисперсия случайной величины ДИ). Это среднее значение квадрата отклонения случайной величины от ее математического ожидания (Тср). Дисперсия - это мера разброса значений случайной величины, Она характеризует степень рассеяния возможных значений случайной величины около ее среднего значения. Численно дисперсия равна математическому ожиданию квадрата разности между самой случайной величиной и ее математическим ожиданием:
(25)
Теоретическая формула для Д(t) имеет вид
(26)
. (27)
Среднее квадратичное отклонение. Учитывая, что дисперсия имеет размерность квадрата случайной величины, то для удобства при расчетах применяется аналог дисперсии, но имеющий размерность случайной величины и представляющий собой
(28)
Гамма-процентное значение случайной величины. Это такое значение случайной величины Τγ, вероятность принять которое для случайной величины или превысить его значение равна γ:
(29)
Очевидно, что
(30)
Уравнение для определения Тγ с учетом функции распределения случайной величины F(t) имеет вид (рис. 8)
(31) или
(32)
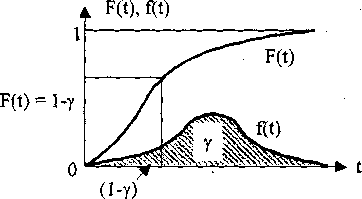
Рис. 8
