В настоящее время не существует общей универсальной теории термоэлектричества, опирающейся на основные положения физики; твердого тела. Это обусловлено тем, что результаты микроскопического подхода в большей мере зависят от тех или иных выбранных модельных представлений о строении вещества и. взаимодействии его частиц между собой. Тем не менее этот подход имеет большое значение для исследования различных механизмов возникновения термо-ЭДС в проводящих средах, а также для объяснения аномалий термоэлектрических свойств металлов и полупроводников.
Термоэлектрические явления в металлах и сплавах. Как известно, металл представляет собой сложную многокомпонентную систему, учитывающую кулоновское взаимодействие электронов с ионами кристаллической решетки и кулоновское обменное взаимодействие валентных электронов.
Упрощенная модель идеального монокристалла металла, в которой регулярно расположенные положительные ионы погружены в «газ» свободных электронов, позволяет рассмотреть термоэлектрические процессы в металлах в первом приближении. В рамках модели предполагается, что плотность электрических зарядов имеет такую величину, при которой в микроскопическом объеме обеспечивается электронейтральность. Электронный газ считается совокупностью невзаимодействующих заряженных частиц со спином 1/2, для которых справедлива статистика Ферми — Дирака. Основные свойства решётки положительных ионов—это пространственная периодичность и точечная симметрия. Ионы колеблются около своих положений равновесия; для описания этого процесса вводят понятие фононов—квазичастиц, которым соответствуют плоские волны. Колебание ионов, обусловленное взаимодействием заряженных частиц, зависящим от времени, приводит к рассеянию электронов вследствие испускания или поглощения ими фононов. Кроме того, взаимодействие частиц характеризуется пространственной периодичностью потенциала решетки и приводит к образованию зон Бриллюэна и возникновению энергетических полос для электронов в твердых телах.
Общие вопросы расчета термоэлектрических свойств металлов детально рассмотрены в работах Дж. Займана, Ф. Дж. Блатта, Р. Бернара, Н. Косака, Ч. Киттеля и др. [45, 13, 76].
Одним из основных механизмов возникновения термо-ЭДС в металлах и металлических сплавах при создании в них градиента температуры является отклонение электронной системы от равновесия. Эта ЭДС называется диффузионной и ее можно рассматривать как результат диффузии заряженных частиц в поле температурного градиента. На диффузионную термо-ЭДС влияет рассеяние носителей тока на фононах, дефектах решетки, примесных атомах, границах зерен и некоторых других микроскопических объектах, а также геометрия поверхности Ферми, температура и другие факторы, определяющие электронный спектр вещества.
Для идеального металла или сплава с изотропным электронным спектром в случае упругого рассеяния электронов с учетом таких микроскопических параметров, как время релаксации и групповая скорость носителей тока, коэффициент термо-ЭДС можно выразить уравнением
![]() (2 .16),
(2 .16),
где ε, τ и ν — энергия, время релаксации и групповая скорость электронов; εf — энергия Ферми; N (ε) — плотность состояний.
Из уравнения видно, что в случае действия одного механизма рассеяния αдиф не зависит от концентрации рассеивающих центров. Диффузионная термо-ЭДС является линейной функцией температуры и доминирует при высоких (Т > 0D, где 0D — температура Дебая) и промежуточных температурах.
Изучению диффузионной термо-ЭДС в металлах посвящено большое количество исследований. Среди них можно отметить вычисления термо-ЭДС для случая простой сферической поверхности Ферми и о учетом различной степени примесного рассеяния Ф. Аттия и И. Ханна в 1964 г. [97]; работу Я. Полака, рассмотревшего в этом же году влияние на величину термо-ЭДС дефектов решетки кристалла [165]. Введение в формулу для диффузионной термо-ЭДС производной по энергии от интеграла по поверхности Ферми было осуществлено Дж. Яном (1968) [1371.
Связь температурного и объемного коэффициентов электросопротивления металлов и диффузионной термо-ЭДС в рамках модели свободных электронов и дебаевского спектра была выведена Р. Барнардом (1971). Его исследования указали на важность учета изменения энергии Ферми при применении постоянной электрон-фононного взаимодействия [100].
Выражение для дифференциальной термо-ЭДС металлов с квадратичным законом дисперсии в кубической решетке получено А. М. Ермолаевым (1972). Он определил, что при температурах, значительно больших или значительно меньших температур Дебая, термо-ЭДС не зависит от изотопического состава, им было также найдено соотношение подобия, связывающее термо-ЭДС идеального металла и металла с произвольным изотопическим составом [42]. Диффузионная термо-ЭДС чистых благородных и щелочных металлов определяется при высоких температурах (Т≥0D) электрон-фононным взаимодействием. В этом случае для модели квазисвободных электронов уравнение для термо-ЭДС имеет вид
![]() (2-17)
(2-17)
Эта формула, несмотря на то что ее вывод основывается на приближенной модели, позволяет правильно оценить порядок величины термо-ЭДС непереходных металлов при высоких температурах, а также с достаточной степенью точности описать ее температурную зависимость.
В частности, об этом свидетельствуют данные В. Роува и П. Шредера (1970) [13]. Однако выражение (2.17) определяет отрицательный знак диффузионной термо-ЭДС для непереходных металлов со сферической поверхностью Ферми. Экспериментальные значения для меди, золота, серебра, лития, кальция, цинка, кадмия имеют положительный знак. Современная теория связывает эти несоответствия теории и эксперимента с несферичностью поверхности Ферми, а также с изотропией электронного рассеяния и электрон-электронным взаимодействием.
Подробный анализ причин расхождения между теоретическими представлениями и реально наблюдаемыми значениями термо-ЭДС в этой группе металлов представлен в работах, выполненных М. Цудзи (1958), П. Клеменсом (1960), Дж. Робинсоном (1967), А. Хасегавой и Т. Касуя (1968), В. Леонардом (1976), Р. Боурассой, С. Вангом и Б. Ленгелером (1978) и др. [13, 107, 147, 183].
Одно из объяснений аномальной положительной термо-ЭДС металлов первой группы было представлено советскими физиками под руководством М. В. Ведерникова на 1-й Международной конференции по термоэлектрическим свойствам металлических проводников (Ист Лэнсинг, США, 1977). Было показано, что аномалия частично обусловливается неквадратичностью электронного спектра в окрестности поверхности Ферми [186].
Термоэлектрические свойства переходных металлов детально рассмотрены в цикле работ П. Нильсена и П. Тейлора, проведенных в 60—70-е годы. Большое внимание этим вопросам было уделено в исследованиях, выполненных под руководством Блатта [13].
Ряд важных изысканий по термоэлектрическим явлениям в магнитоупорядоченных (ферромагнитных и антиферромагнитных) переходных металлах провели советские физики. Так, в 1963 г. Л. Э. Гуревичем и И. Я. Коренблитом установлено, что в металлах этого типа проявляется еще один механизм термо-ЭДС — термо-ЭДС магнонного увлечения, связанного с рассеянием электронов на спиновых волнах. Установлено, что при низких температурах величина αмагн должна изменяться пропорционально Т3/2 в ферромагнетиках и Т3 в антиферромагнетиках. Основной вклад в термо-ЭДС железа при низких температурах вносит αмагн. Кроме того, эффект магнонного увлечения, играющий существенную роль в термо-ЭДС лантаноидов, является одной из причин немонотонной зависимости термо-ЭДС от температуры в области низких температур [34].
Ш. Ш. Абельским и И. Я. Коренблитом (1979) была вычислена термо-ЭДС в магнитном поле с учетом анизотропной щели, возникающей в спектре энергии электронов проводимости в области антиферромагнитного упорядочения. Полученный результат показал, что появление щели уменьшает термо-ЭДС. Воздействие магнитного поля сначала приводит к минимальному значению термо-ЭДС, после чего дальнейшее возрастание напряженности повышает коэффициент термо-ЭДС [1].
Большое количество работ было посвящено расчету термо-ЭДС сплавов. В частности, Ж. Фридель (1953) вычислил термо-ЭДС в сплавах в зависимости от концентрации составляющих. У сплавов на основе алюминия и сплавов переходных металлов изменение термо-ЭДС пропорционально разности валентностей основной составляющей и примеси [128].
Теоретический анализ термо-ЭДС сплавов у Ч. Доменикали (1960) основывался на предложенной им модели резонансного рассеяния электронов на атомах примесей в кристаллической решетке. Эта модель предполагает существование достаточно узкой области температур, в которой в зависимости от сорта примесей наблюдается либо резонансное возрастание, либо резонансное уменьшение времени релаксации электронов проводимости [121].
Изучение переходных металлов как растворителей и примесей было проведено Д. Мак-Дональдом, В. Пирсоном и И. Темплетоном (1962). В рамках приближения почти свободных электронов при низких температурах помимо упругого рассеяния электронов на примеси существенное значение имеет неупругое, возникающее за счет s — d- взаимодействия [154].
Д. Торнтон, В. Янг и А. Мейер (1968) рассчитали диффузионную термо-ЭДС сплавов щелочных металлов друг с другом при низких температурах на основе теории псевдоатомного экранирования. Впервые знаки экспериментальных и теоретических термо-ЭДС совпали [180].
Термо-ЭДС разбавленных магнитных сплавов с помощью теории возмущений вычисляли Б. Хорватия и В. Златич (1979). Рассмотрев систему, описываемую одноорбитальной моделью Андерсена без предположения об электрон-дырочной симметрии, они установили, что в линейном члене разложения по температуре усиление термо-ЭДС, обусловленное кулоновскими корреляциями, совпадает с аналогичным вкладом в теплоемкость [136].
Термоэлектрические явления в полупроводниках. Основы современной микроскопической теории термоэлектрических эффектов в полупроводниках, как уже отмечалось, были заложены в 30-х годах. Однако следует признать, что единый общий подход к описанию термоэлектрических свойств полупроводниковых систем с учетом различных условий пока не разработан. Подробное рассмотрение отдельных вопросов микроскопической теории термоэлектричества в чистых полупроводниках и полупроводниковых сплавах представлено в ряде обзоров и монографий Л. С. Стильбанса, А. И. Ансельма, Б. И. Аскерова, Дж. Ная, Я. Тауца, А. Ф. Иоффе, В. А. Джонсона, К. Ларк-Горовитца, Ч. Киттеля, Д. А. Райта, Р. Смита, М. С. Соминского, Дж. Драббла, Г. Голдсмидта, В. Шокли, К. Зенера, П. С. Зырянова, Г. И. Гусевой [6, 36, 43].
Основные положения теории термо-ЭДС в полупроводниках можно описать на примере последовательного изложения этого вопроса, представленного Л. С. Стильбансом [83]. Коэффициент термо-ЭДС полупроводника с произвольной степенью вырождения в случае одного сорта носителей, параболической зонной структуры, степенной зависимости длины свободного пробега от энергии выражается уравнением вида
![]()
(2.18)
где μ* = μ/kT — приведенный химический потенциал; r — показатель степени, характеризующий зависимость длины свободного пробега электрона от его энергии; Fr(μ*), Fr+1 (μ*) — интегралы Ферми
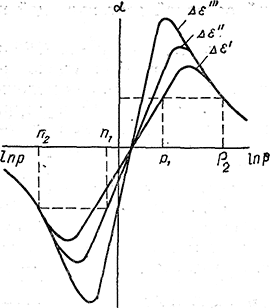
Рис. 2.2. Зависимость термо-ЭДС от концентрации носителей в области смешанной проводимости для полупроводников с различной шириной запрещенной зоны ![]() [83].
[83].
![]() . (2.19)
. (2.19)
Приведенный химический потенциал μ* связан с концентрацией носителей соотношением
![]() . (2.20)
. (2.20)
Зависимость термо-ЭДС от температуры и концентрации носителей определяется с учетом выражения (2.20) формулой
![]()
Это выражение справедливо для невырожденных полупроводников, для которых n —2.
Характер кривых на рис. 2.2 определяется соотношением подвижностей и эффективных масс электронов и дырок, может также зависеть от механизмов рассеяния электронов и дырок. Максимальные значения термо-ЭДС обратно пропорциональны ширине запрещенной зоны. Величина термоэлектродвижущей силы зависит от вида энергетического спектра электронов и дырок.
Разнообразие полупроводниковых систем, их микроскопических параметров и внешних воздействий объясняет то огромное количество работ, которое посвящено исследованию термоэлектрических эффектов в полупроводниках. Элементарный вывод точного выражения для термо-ЭДС в невырожденном полупроводнике приведен в работах С. Херринга (1953) [134], И. Прайса (1955—1956) [166], И. Аппеля (1957) [95], О. Маделунга (1958), С. Аоки (1960) [43]. Вопросы температурной зависимости термо-ЭДС примесных полупроводников исследовались Т. А. Конторовой. Теорию термоэлектричества двухзонных полупроводников развил Э. Хага (1959). М. Цудзи (1959) исследовал термоэлектрические свойства полупроводников на основе модели локализованных электронов. Влияние областей пространственного заряда на величину термо-ЭДС в полупроводниках рассмотрев . Т. Ота (1960). Р. Миллер, Р. Хейкес и Р. Мазельский (1961) проанализировали термоэлектрические явления в полупроводниках со смешанной проводимостью [43]. Применение метода дрейфовой скорости к изучению термоэлектрических явлений в полупроводниках было осуществлено Ф. F. Серовой (1962) [82].
Теорию термо-ЭДС в полупроводниках с малой подвижностью, в которых носители локализованы из-за поляризации решетки, разработали М. Чадда и А. Синха (1963). Термо-ЭДС в полупроводниках с учетом экранированных кулоновских полей примесных ионов вычислил М. Ереженов (1964). Он показал, что введение заряженных примесей увеличивает термо-ЭДС. Л. Эйзенберг (1965) рассчитал модуляцию термо-ЭДС в электрическом поле тонкопленочного полупроводника. Л. Фишер и Р. Вагнер (1966) изучили термоэлектрический циклотронный резонанс. С. Шарма (1967) посвятил свои исследования вычислению абсолютной термо-ЭДС в вырожденном полупроводнике [36].
Н. В. Коломоец рассчитал термоэлектрические свойства вещества с учетом влияния межзонных переходов (1966) [54]. Влияние размерного эффекта на термоэлектрические явления в полупроводниковых пленках рассмотрел Ю. Кремпарский (1969) [142]. Термоэлектрические свойства тонких слоев полупроводника исследовались также В. Г. Полниковым (1973) [73]. Термо-ЭДС слаболегированных полупроводников в области прыжковой проводимости была рассчитана О. А. Голиковой и В. В. Косаревым (1974) [28, 58]. Теоретическое рассмотрение термо-ЭДС бесщелевых полупроводников в условиях резонансного рассеяния электронов на акцепторном уровне провели В. К. Дугаев и Π. П. Петров (1979) [41].
Учет эффектов увлечения. Как известно, на кинетические свойства твердых тел заметное влияние оказывают так называемые эффекты увлечения: взаимное увлечение электронов и фононов, увлечение одноименных по знаку заряда носителей в греющих электрических полях, увлечение электронов потоками дефектов и др. Наиболее изученным из них является электрон-фононное увлечение, представляющее значительный интерес для исследования термоэлектрических свойств твердых тел при низких температурах.
Эффект увлечения электронов потоком фононов, создаваемым градиентом температур, открытый Л. Э. Гуревичем, обусловлен асимметричным рассеянием потока электронов на колебаниях решетки при наличии температурного градиента, в результате электроны проталкиваются фононами к холодному концу образца. Согласно экспериментальным данным термо-ЭДС при температурах ниже 200 К существенно превышают значения, рассчитанные по формулам для термо-ЭДС полупроводника, полученным Μ. П. Бронштейном и Р. Фаулером в 30-х годах [40]. Теоретический анализ отношения между электронной составляющей термо-ЭДС ае и компонентой, возникающей вследствие увлечения электронов фононами щ, провели X. Фредерикс (1953), К. Херринг (1953), Д. Терхаар и А. Нивз (1954, 1955). Кроме того, Херринг (1954) установил зависимость длины свободного пробега фононов от температуры и импульса, при этом величина α оказалась пропорциональной Τ-7/2. Экспериментальные данные достаточно хорошо согласовывались с этим результатом.
При очень низких температурах время релаксации, связанное с рассеянием фононов на границе образца, становится меньше по сравнению современен релаксации при взаимном рассеянии фононов. Это приводит к резкому падению величины, которая при приближении к абсолютному нулю температуры асимптотически стремится к нулю [134].
Теория Херринга обладала рядом существенных недостатков, что накладывало определенные ограничения на ее применение. В ней не выполнялся принцип симметрии Онсагера, что привело к ошибкам в решении кинетических уравнений для электронной и фононной функций распределения, В эффекте увлечения проявляется неравновесный характер электронной и фононной подсистем, поэтому их описание необходимо проводить с привлечением основных принципов термодинамики необратимых процессов, как это было впервые осуществлено в 1956 г.
Э. Сондхеймером [40].
Многочисленные исследования электрон-фононного увлечения шли по двум направлениям: первое изучало этот процесс в металлах, второе — в полупроводниках. Наиболее полно влияние фононного увлечения на термоэлектрические свойства в металлах раскрыто в монографии Ф. Дж. Блатта, П. А. Шредера, К. Л. Фойлза и Д. Грейча «Термоэлектродвижущая сила металлов» [13], в которой авторы обобщили теоретические и экспериментальные исследования, проведенные разными физиками, за период с конца 50-х до начала 70-х годов. Общие соотношения, описывающие термо-ЭДС фононного увлечения, были получены в серии работ М. Байлина. Полученные им выражения оказались сложны для вычисления, так как для этого необходимо знание закона дисперсии, вероятностей переходов электрона из одного состояния в другое, различных процессов рассеяния фононов, скоростей электронов на известной поверхности Ферми. Более удобное уравнение для расчета термо-ЭДС фононного увлечения предложено авторами упомянутой выше монографии. Анализ влияния эффекта увлечения на термо-ЭДС при высоких температурах, когда преобладает фонон-фононное взаимодействие, проведен Клеменсом (1958) и Блаттом (1964, 1968), установившими, что Т3. При низких температурах величина термо-ЭДС фононного увлечения пропорциональна решеточной теплоемкости, что приводит к зависимости αф ~ Т3.
В наиболее чистом виде пропорциональность термо-ЭДС фононного увлечения Т3 проявляется в щелочных металлах, широкие исследования которых были предприняты в 1958—1963 гг. Д. Мак-Дональдом, А. Гено, В. Пирсоном, И. Темплетопом.
Измерения термо-ЭДС фононного увлечения в других металлах не подтвердили строгого выполнения закона Т3. Из экспериментальных работ в этой области можно упомянуть исследования В. Пирсона (1960); В. ван Баарле, К. Роуста, Ф. Гортера (1966), А. Гено (1967) на серебре, В. Воробея, П. Линденфелда и В. Б. Серина (1965) на золоте; Де Фроомена, В. ван Баарле и А. Кыолине (1960), Г. Боато и Дж. Вига (1967), Р. Авербака, С. Стефана и Дж. Басса (1973) на сплавах алюминия; И. Пембертона и Гено (1971) — на сплавах меди, А. Голде и В. Пирсона (1963)— на свинце. В. Роув и П. Шредер (1970) исследовали термо-ЭДС магния, кадмия и цинка, А. Каплин, С. Чианг, П. Шредер и Дж. Трейси (1971)— индия; С. Махаян, Дж. Даунт, Р. Боингтон и М. Якуб (1973) — галлия.
Как отмечал Блатт, расхождения экспериментальных данных с теорией в первую очередь связаны с тем, что в этих металлах при низких температурах на величины термо-ЭДС влияют процессы переброса, которые обычно не учитывались в теоретической модели (первые попытки расчета термо-ЭДС с учетом процессов переброса были осуществлены И. Байлиным (1958), Дж. Займаном (1959) и П. Клеменсом (1960) [13, 76].
В современной теории термо-ЭДС в металлах большую полемику вызывает вопрос о так называемом ложном фононном увлечении. Обычное фононное увлечение определяется процессами рассеяния первого порядка, при которых фононы поглощаются или испускаются. Кроме них, существуют процессы второго порядка с промежуточными фононными или электронными состояниями, в которых могут находиться частицы или дырки. Как показали исследования П. Нильсена и П. Тейлора (1968—1974), члены второго порядка существенно зависят от энергии, вследствие чего они должны быть учтены при расчете термо-ЭДС. На простой модели рассеяния электронов на фононах и примесях Нильсон и Тейлор вычислили для этих процессов поправки второго порядка к вероятности рассеяния для чистых металлов и разбавленных твердых растворов. По теореме советского физика А. Б. Мигдала (1958) эти поправки составляют очень малое значение и изменяют вероятность рассеяния на величину порядка (1 + т/М), где т — масса электрона, а М — масса фонона. Однако вблизи уровня Ферми поправки второго порядка зависят от энергии и при определении термо-ЭДС, по мнению Нильсена и Тейлора, учет характера изменения зависимости вероятности рассеяния от энергии является очень важным. Функциональная форма этой зависимости изменяется с температурой; при низких температурах вклад этих процессов в термо-ЭДС пропорционален Т3, при высоких — T-1. Такая температурная зависимость присуща термо-ЭДС, обусловленной фононным увлечением, поэтому этот эффект получил название ложного фононного увлечения, или эффекта Нильсена — Тейлора. Экспериментальное наблюдение этого эффекта чрезвычайно затруднено, так как трудно установить различие между истинным и ложным фононным увлечениями из-за одинаковой температурной зависимости. В настоящее время нет достаточных экспериментальных данных, чтобы считать эффект Нильсена — Тейлора либо доказанным, либо опровергнутым. Лишь более точные расчеты термо-ЭДС фононного и ложного увлечения с учетом всех видов взаимодействия в системе могут привести к правильному толкованию опытных данных [13].
В полупроводнике эффект увлечения электронов фононами оказывает более значительное влияние на термо-ЭДС, чем в металле.
Работы но расчету термо-ЭДС, обусловленной взаимодействием электронов и фононов, в зависимости от использовавшегося подхода при вычислении этой величины можно разделить на две группы. Первый, получивший название α-подхода, основан на определении электрического тока, возникающего при увлечении носителей тока потоком фононов. Этот подход использовался в первых работах Л. Э. Гуревича, X. Фредерикса, Дж. Паррота, Д. Мак-Дональда. Второй
(π-подход) подход связан с вычислением теплового потока фононов, вызываемого электрическим током. Впервые такой метод расчета был предложен в 1953 г. С. Херрингом и уточнен в 1954 г. П. Клеменсом [83].
Теория термоэлектрических явлений в полупроводниках с учетом эффекта увлечения постоянно развивается. Изучение термоэлектрических явлений при низких температурах, когда существенную роль играют эффекты увлечения, привлекает к себе постоянное внимание физиков не только тем, что позволяет глубже исследовать природу термоэлектричества, но и тем, что анализ термоэлектрических свойств с учетом эффекта увлечения наряду с опытами по поглощению ультразвука и измерением теплопроводности представляет эффективный метод определения времени релаксации различных частей фононного спектра. Расширяется также класс материалов, на которых экспериментально исследуется эффект увлечения. Так, Р. Мэнсфилд и С. Садам в 1953 г. обнаружили термо-ЭДС увлечения на MoSi2 р-типа; X. Фредерикс и Э. Милзарек измерили этот эффект в InSb р-типа, в 1955 г. Я. Н. Тимошенко и С. С. Шалыт наблюдали эффект на теллуре, а Г. Голдсмит и Д. Райт — на алмазе в 1959 г. В этом же году термо-ЭДС фононного увлечения была обнаружена в экспериментах А. Хатсона на ZnO и CdS в измерениях К. Морикавы [85, 113].
В разработке теории термо-ЭДС полупроводников с учетом эффекта увлечения участвовали многие физики. Особо следует выделить работы таких советских исследователей: Е. Джакасимова, В. Л. Гуревича и Ю. А. Фирсова, Е. Н. Агафоновой и Н. И. Лычагина, А. А. Натадзе и А. Л. Эфроса, В. С. Сардаряна, И. С. Будни А. Г. Самойловича и др. [36, 43, 78, 79].
В настоящее время в теории термоэлектричества различают два эффекта фононного увлечения в полупроводниках — обычный, или нормальный, эффект увлечения электронов фононами и двухступенчатое увлечение электронов фононами. Второй тип эффекта впервые описан в работах советских физиков В. А. Козлова, Н. С. Лидоренко и Э. Л. Нагаева в 1971 —1972 гг. 152, 53]. Согласно разработанной ими теории двухступенчатое увлечение электронов фононами возникает в условиях гидродинамического точения тепловых фононов. Электроны проводимости в полупроводниках увлекаются, как известно, длинноволновыми фононами, которые в свою очередь увлекаются тепловыми фононами. Это приводит к двухступенчатому характеру увлечения, причем неравновесная часть электронной функции распределения главным образом определяется тепловыми фононами. Вследствие этого термо-ЭДС увлечения в толстых образцах экспоненциально возрастает при понижении температуры. В тонких образцах рассеяние электронов и фононов на их поверхности обусловливает падение термо-ЭДС с уменьшением температуры, однако характер зависимости термо-ЭДС от температуры и толщины образца отличается от характера этой же зависимости при обычном эффекте увлечения. Опыты авторов на висмуте, а также экспериментальные данные по графиту, полученные в 1977 г.
О. Сугихарой, X. Охшимой, К. Кавамурой и Т. Цузуку, подтвердили существование нового механизма увлечения и его влияния на термоэлектрические свойства полупроводников [173].
Термо-ЭДС металлов и полупроводников в магнитном поле. Изучение зависимости термо-ЭДС металлов от напряженности магнитного поля имеет прикладное и фундаментальное значение. Исследование этого вопроса очень важно при разработке термопар, предназначенных для измерения температур в магнитных полях. Кроме того, теоретический и экспериментальный анализ поведения термо-ЭДС металлов в магнитных полях представляет широкие возможности для исследования структуры металлов, их свойств и параметров.
Первые широкие исследования в этой области предприняты Д. Мак-Дональдом и В. Пирсоном (1957). Они определили изменение термо-ЭДС меди и натрия под действием магнитного поля. Следует отметить, что это выполнялось тогда, когда сверхпроводники второго рода (широко применяющиеся в настоящее время в сверхпроводящих соленоидах для получения сверхмощных магнитных полей) еще не были известны. Индукция магнитных полей, использовавшихся в экспериментах Мак-Дональда и Пирсона, не превышала 1,2 Тл. По этой причине, а также вследствие невысокого уровня измерительной техники того времени не была достигнута необходимая точность измерений, и их результаты в основном сводились к порядку величин и знаку наблюдаемых эффектов. По заключению исследователей, влияние магнитного ноля на одновалентные металлы независимо от знака проявляется в возрастании термо-ЭДС до абсолютной величине [13].
Исследование влияния поперечного магнитного поля на термо-ЭДС алюминия провели Р. Авербак и Дж. Басс, С. Стефан (1971). В этих экспериментах вторую ветвь термопары представлял сверхпроводник второго рода, что при температурах ниже критической обеспечивало возможность определения абсолютной термо-ЭДС алюминия. В этом случае термо-ЭДС представляла собой сумму двух слагаемых, одно из которых зависело от температуры по линейному закону, другое было пропорционально T3. Первое слагаемое соответствовало диффузионному вкладу в термо-ЭДС, второе определялось фононным увлечением. Обе указанные величины зависели от величины магнитного поля, причем наиболее сильная зависимость свойственна диффузионной термо-ЭДС, которая в сильных полях изменяла знак и обнаруживала насыщение.
С. Стефан и Дж. Басс измерили также термо-ЭДС разбавленных твердых растворов на основе алюминия с добавкой меди, титана, олова и кадмия. Несмотря на то что диффузионная термо-ЭДС в отсутствие поля а (О, Т) очень чувствительна к концентрации примеси, разность ∆аd (H, Т)=α (Н, Т) — аа (0, Т) при Н→∞ имела практически одно и то же значение для всех сплавов. Теоретическое толкование этого явления на основе полуклассического подхода было представлено Р. Авербаком и Д. Вагнером (1972). Их теория носила качественный характер и предсказанное ими значение величины Δа было примерно в два раза меньше экспериментального. Позднее Ф. Блатт с сотрудниками вывели формулу для
∆а (Н, Т), справедливую для всех значений напряженности магнитного поля.
Изучение термоэлектрических свойств полупроводников в магнитном поле тесно связано с исследованием механизмов рассеяния в твердых телах и определением времени релаксации носителей заряда. Одной из первых работ в этом направлении явилось исследование И. Аппеля (1959). Он теоретически рассмотрел вопрос об определении времени релаксации для взаимодействия фононов, причем в его выражение входила константа, которая могла быть рассчитана по данным измерений температурной зависимости термо-ЭДС в магнитном поле [95].
В собственном полупроводнике, как показал П. Прайс (1956), воздействие магнитного поля изменяет отношение подвижностей носителей тока, что приводит к изменению соотношения электронной и дырочной электрических проводимостей и, следовательно, к изменению термо-ЭДС. В случае несобственного полупроводника термо-ЭДС зависит от средних значений кинетической энергии, переносимой электронами и дырками. В сильных магнитных полях изменение термо-ЭДС происходит также за счет изменения химических потенциалов электронов и дырок [85].
Теория термо-ЭДС полупроводников в магнитном поле была разработана С. Херрингом, Т. Гебалле и Дж. Канзлером (1958). Они установили, что для слабых магнитных полей изменение термо-ЭДС всегда пропорционально квадрату магнитной индукции, в сильных полях оно достигает насыщения. Измерения, проведенные М. Стилом (1957) на германии, подтвердили этот вывод [85].
В ходе исследований, проведенных М. Родо (1960), И. В. Мочаном, ΙΟ. Н. Образцовым и Т. В. Смирновой (1962), установлено, что в сильном магнитном поле термо-ЭДС не зависит от механизма рассеяния. Это позволяет измерять эффективную массу носителей тока с точностью большей, чем в случае определения эффективной массы по термо-ЭДС без магнитного поля [9].
Термоэлектрические явления в квантующем магнитном поле. Движение заряженной частицы (электрона) в магнитном поле с точки зрения квантовой механики впервые исследовал Л. Д. Ландау в 1930 г. [9]. Он установил, что спектр электрона в однородном магнитном поле носит дискретный характер, т. е. круговое движение электрона в плоскости, перпендикулярной вектору напряженности магнитного поля, квантуется. Квантование электронных орбит в магнитном поле обусловливает осцилляцию всех электронных свойств металлов при выполнении условий ωτ > 1 и kТ < βH (здесь β == eh/m*c).
В реальных кристаллах β и ω зависят от ориентации магнитных силовых линий относительно кристаллографических осей, поэтому квантовые эффекты могут проявляться только в монокристаллах. Кинетические свойства металлических монокристаллов также отчетливо проявляют выраженную анизотропию, тесно связанную с особенностями топологии поверхности Ферми.
Термоэлектрические свойства металлов, находящихся в квантующем магнитном поле, характеризуются некоторыми особенностями по сравнению с другими явлениями переноса. Осцилляции электронных свойств связаны с тем, что по мере изменения напряженности магнитного поля квантованные уровни Ландау последовательно проходят через уровни Ферми, что обусловливает изменение плотности состояний вблизи энергии Ферми с периодичностью, пропорциональной ПН. Эта периодичность, в свою очередь, отражается на физических свойствах металлов, зависящих от плотности состояний N (η), таких, как удельная теплоемкость, магнитная восприимчивость, электросопротивление.
Согласно теории квантовых осцилляций термоэлектрических эффектов, впервые разработанной советским исследователем Г. Е. Зильберманом в 1955 г., термоэлектрические параметры в отличие от других физических свойств определяются не N (η), а производной N (ε) по энергии, взятой при ε = η. Таким образом, в то время как, например, осцилляции электропроводности (эффект Шубникова — де Гааза) накладываются на большой фон магнетосопротивления, осцилляции термо-ЭДС и коэффициента Пельтье, обусловленные квантованием уровня Ландау, происходят между положительным и отрицательным экстремальными значениями. Благодаря этому амплитуды осцилляции значительно превышают среднюю термо-ЭДС и средний коэффициент Пельтье.
Осцилляционные термоэлектрические эффекты впервые экспериментально обнаружены на висмуте М. Стилом и Дж. Бабискиным (1955), а также С. Греньером, Дж. Рейнольдсом и Дж. Сибертом (1963). Вторая группа исследователей совместно с Дж. Лонгом (1965) изучала осцилляции термо-ЭДС в сурьме. Подобные исследования на олове провел Дж. Вуллман (1969), на алюминии — В. Вестернич и С. Папастейкуемдис (1974). Осцилляции коэффициента Пельтье были обнаружены X. Тродалом и Ф. Блаттом (1969) на цинке [13].
Изменение термо-ЭДС полупроводников в квантующих магнитных полях явилось предметом многочисленных исследований в 60-х годах. Особое внимание этому вопросу было уделено советскими физиками. Первые исследования термо-ЭДС в поперечном квантующем поле выполнили А. И. Ансельм и Б. М. Аскеров (1960, 1961), Л. Э. Гуревич и Г. М. Недлин (1961), М. И. Клингер (1961) [9]. Их результаты противоречили соотношению Эйнштейна и положениям термодинамики. Эти противоречия были устранены теорией Ю. Н. Образцова (1964, 1965), установившей, что при расчете термоэлектрических свойств в квантующих магнитных полях необходимо учитывать эффекты, связанные с магнитным моментом, вызванным квантованием движения электронов, т. е. следует ввести в описание диамагнетизм Ландау [67]. В дальнейшем данные результаты использовались в работе А. И. Ансельма, Ю. Н. Образцова и Р. Г. Тарханяна (1964) по вычислению термо-ЭДС в полупроводниках с непараболической зоной, в работе В. С. Воробьева (1965), в которой рассматривались многоэллипсоидные полупроводники, а также в исследованиях К. Д. Цэндина и А. Л. Эфроса (1966) по теории термо-ЭДС в квантующем магнитном поле в модели Кейна [9, 36].
Важную особенность термоэлектрических явлений в квантующем магнитном поле представляют собой проявляющиеся в них многочастичные эффекты, т. е. в отличие от других явлений переноса для термо-ЭДС существенны поправки на увеличение эффективной массы электрона, обусловленные его взаимодействием с фононом. Как установлено работами Дж. Опсала, Дж. Басса и В. Талера (1976,1978), С. Лайоу (1977, 1978), А. Виленкина, И. Оно, Р. Тейлора (1978, 1980), многочастичные эффекты и связанное с ними увеличение массы электрона, а также перенормировка скорости, энергии, времени релаксации квазичастиц занимают важное место среди других механизмов возникновения термо-ЭДС. Детальное исследование этих процессов и их влияние на термоэлектрические свойства твердых тел определяют дальнейшее развитие этого направления теории термоэлектричества [13, 95, 153, 161, 162].
Другие направления теории термоэлектричества. Теория термоэлектричества не ограничивается рассмотренными выше вопросами, а охватывает широкий круг проблем, исследование которых имеет большое фундаментальное и прикладное значение.
Одну из важных областей теории термоэлектричества представляют термомагнитные явления в металлах и полупроводниках, анализ которых является эффективным методом исследования энергетического спектра носителей тока и фононов, характера их взаимодействия, особенностей различных микропроцессов, протекающих в твердом теле, а также определения важнейших параметров полупроводников: концентрации, эффективной массы, длины свободного пробега носителей тока и т. п.
Теория термомагнитных эффектов включает вопросы поведения неизотермических металлов, полуметаллов и полупроводников в слабых, сильных классических полях и квантующих магнитных полях, рассматривает особенности эффектов в зависимости от свойств объемных и пленочных структур, преобладания того или иного механизма рассеяния, учета эффектов увлечения, анизотропии и др. Актуальными стали проблемы прохождения через неизотермическую среду электромагнитных волн, исследуемые в нашей стране под руководством Л. Э. Гуревича (1965, 1980) [33]. Новый термомагнитный размерный эффект обнаружили советские физики Б. В. Авдеев, Н. И. Варич, Ю. П. Крашенинин, М. А. Маркман и Э. Л. Нагаев (1970). Этот эффект возникает в неравномерно нагретом образце, помещенном в переменное магнитное поле, и связан с деформацией вихревых токов, наведенных переменным полом. Тот факт, что величина эффекта пропорциональна производной от проводимости образца по температуре, делает его приемлемым для исследования электрических свойств проводников вблизи точки фазового перехода [2].
Как отмечалось выше, термомагнитные эффекты лежат в основе работы ряда термоэлементов, перспективных для получения глубокого охлаждения, использования в качестве источников тока и приемников излучения. Определяющую роль в формировании этого направления развития теории термоэлектричества сыграли работы советских физиков И. М. Цидильковского, Ф. Г. Басса, Ю. Н. Образцова, Б. М. Аскерова, А. И. Ансельма, П. С. Зырянова, К. Б. Толпыго, Г. Е. Пикуса, М. И. Клингера, Ш. Ш. Абельского, Я. Агаева, О. Мосанова, М. Д. Блоха, Е. Джаксимова и др. [4, 6, 14, 22, 36, 43, 92]. Среди зарубежных исследователей следует выделить Д. Райта, П. Прайса, Г. Голдсмита, Дж. Паррота, Л. Сосновского, Т. Хармана, Дж. Хонига, И. Оно, Р. Фиески [36, 43, 132].
Отдельное направление теории термоэлектричества представляет пьезотермоэлектричество, т. е. термоэлектрические явления, возникающие при механическом воздействии на неизотермическую среду. К первым исследованиям в этой области относятся работы, выполненные Дж. Драбблом (1958), С. Д. Герцрикеном, Η. Н. Новиковым и В. С. Копанем (1959) [25, 122]. В теории пьезотермоэлектричества важное место занимают работы советских физиков Л. И. Анатычука, В. Д. Искры, П. И. Баранского, И. С. Б уды, А. Г. Самойловича, В. В. Лебедева и др. [6]. За рубежом этой проблемой занимались Р. Тиндер и К. Кунду [144].
Особое место среди исследований в области теории термоэлектричества занимают термоэлектрические явления в сверхпроводниках, начатые в 1935—1938 гг. Первые наблюдения эффекта Зеебека в цепи из сверхпроводника и нормального металла были проведены К. Стейнером, П. Грассманом, Дж. Коком, В. Кеезом и С. Маттисом [80]. Ряд фундаментальных исследований провел В. Л. Гинзбург [26, 27]. Особо интенсивные исследования в этом направлении проводились в 70—80-е годы. Неслучайно на 1-й Международной конференции по термоэлектрическим свойствам металлических проводников (Ист Лэнсинг, США, 1977) сверхпроводникам были посвящены шесть докладов, два из которых представлены Г. Ф. Жарковым, А. М. Гуляном и Π. Н. Лебедевым [178].
Большой интерес у физиков вызывают термоэлектрические явления в проводящих средах с неравновесной концентрацией носителей. Эта область теории термоэлектричества включает исследование эффектов в переходах, в условиях больших градиентов температур и разогрева носителей полем сверхвысокой частоты и т. п. Исследования в этом направлении не только углубляют современные знания в области физики твердого тела, но и расширяют представления о термоэлектрическом методе преобразования энергии, определяют новые пути конструирования эффективных преобразователей.
Термоэлектрические явления в присутствии потенциального барьера изучали Дж. Гренвилл и А. Хогарт (1951), Я. Тауци и З. Троусил (1953, 1957), Р. Холл (1958, 1961), М. Катлер (1961), Р. Юр (1962), М. Медехи (1962), В. Буллис (1963) [85, 114, 185]. Среди последних работ этому вопросу посвящены исследования Г. Дадамирзаева (1973), А. И. Вейнгера и Э. А. Акопяна (1975) и др. [19, 38].
Фундаментальные исследования термоэлектрических эффектов при больших градиентах температур выполнили Я. Тауц с сотрудниками в 50 — начале 60-х годов [85]. В созданной ими теории исследовались явления, вызванные диффузией неосновных носителей тока в низкотемпературную область образца, которые при достаточно больших градиентах температуры оказались неравновесными. Подобные условия реализуются в полупроводниках типа германия и кремния при ∆Т ~ 102 ~ 103 К/см. Результаты теории были экспериментально подтверждены 3. Троусилом [85].
Советскими физиками Л. И. Анатычуком, Л. П. Булатом, Е. Н. Комоловым и другими (1977, 1978) был рассмотрен второй возможный механизм влияния большого градиента на кинетические явления в полупроводниках. Они доказали, что при более высоких градиентах, при которых еще выполняется неравенство (L0 — длина остывания электрона, LТ= Т | ∆Т1 | — характерная длина изменения температуры) коэффициент термо-ЭДС становится функцией градиента температуры [7]. В работах этих авторов исследуется разогрев электронного газа за счет теплового потока. Заметим, что разогрев носителей может осуществляться также СВЧ полем. Термоэлектрические эффекты, возникающие в таких условиях, детально изучаются в основном советскими физиками. В частности, С. Ашмоктасом, Г. Дадамирзаевым, А. Тешабаевым, А. И. Вейнгером, Μ. П. Саргсяном, Ю. К. Пожелой [20, 72, 86 и др.]. Прикладные аспекты термоэлектрических эффектов в среде с «горячими» электронами рассмотрены в работе В. М. Светличного, В. Т. Плаксин, О. А. Пересунько [81].
В самостоятельное направление теории термоэлектричества можно объединить работы по термоэлектрическим и термомагнитным эффектам в ограниченных полупроводниках Ф. Г. Басса, М. И. Каганова, В. С. Бочкова, Ю. Г. Гуревича, М. Я. Грановского, З. С. Грибникова, А. М. Конина и др. [11, 29, 56]. Учет конечности размеров образца позволяет получить более точные оценки термоэлектрических и термомагнитных свойств полупроводников, что является существенным для совершенствования теории расчета термоэлектрических приборов различного назначения.
Актуальную область теории представляет также анализ термоэлектрических свойств неупорядоченных систем. Это связано с более широким практическим применением жидких и аморфных полупроводников, сильнолегированных полупроводников, жидких металлов. Сюда примыкают исследовании полупроводников, подвергнутых действию облучения, так как вещество в этом случае становится в определенной мере разупорядоченным. Теоретическим аспектам термоэлектричества в неупорядоченных системах, а также экспериментальным исследованиям по термо-ЭДС в неупорядоченных полупроводниках посвящены многочисленные работы советских и зарубежных физиков, однако к настоящему времени еще не создана теория, объясняющая все опытные данные по термоэлектрическим свойствам таких структур. Наиболее полно теоретическое описание термоэлектрических явлений в неупорядоченных средах представлено в монорафии И. П. Звягина [46].
Использование достижений теории термоэлектричества дает реальную возможность для получения оптимизированных термоэлектрических материалов с заранее заданными свойствами, позволяет совершенствовать принципы конструирования и методику расчета многочисленных термоэлектрических приборов и устройств.

