Феноменологическая теория.
Непрерывное расширение и углубление теоретического описания термоэлектрических явлений тесно связано с развитием многих научных направлений — физики твердого тела, квантовой механики, термодинамики, статистической физики и др. Особую роль в формировании современной теории термоэлектричества сыграла термодинамика необратимых процессов, основы которой разработал в 1931 г. норвежский физико-химик Л. Онсагер [10, 24].
Одной из задач Онсагера при создании новой теории было обоснование предположения Томсона о разделении необратимых и обратимых процессов. Онсагер писал: «Гипотеза Томсона не была основана на общих принципах молекулярной динамики, поэтому необходимо дать обоснование более общему классу соотношений взаимности путем рассмотрения микроскопической обратимости» [24, с. 195]. Для этого ои предложил использовать в «квазитермодинамике» (так он назвал свою новую теорию) принцип динамики частиц, включающий представления о сило и скорости. Для описания причины, вызывающей необратимое явление (температурный градиент, градиент концентрации и пр.), Онсагер ввел понятие термодинамической силы. Эта величина описывала степень отклонения системы от ее термодинамического равновесного состояния. Термодинамическая сила вызывала необратимое явление, характеризуемое термодинамической скоростью (позднее этот термин был заменен другим— «термодинамическим потоком»).
Между термодинамическим потоком, вызываемым термодинамическими силами, и этими силами существует линейная связь:
![]() (2.10)
(2.10)
где Lik — кинетические коэффициенты.
При выборе термодинамических: потоков и сил таким образом, что скорость производства энтропии S* можно выразить как
![]() (2.11)
(2.11)
кинетические коэффициенты подчиняются принципу симметрии Онсагера
![]() (2.12)
(2.12)
Основные соотношения термодинамики необратимых процессов по своей сущности являются макроскопическими, хотя для их вывода использовались микроскопические, обратимые во времени основные уравнения механики. Таким образом, Онсагеру удалось связать посредством представлений статистической механики микро- и макроскопические свойства системы, находящейся в состоянии термостатического равновесия вследствие достаточно долгой изоляции от других сред и систем.
Первоначально положения термодинамики необратимых процессов применялись для подтверждения справедливости соотношения Томсона в рамках новой теории. Такие исследования проводили Н. Мотт (1939), Г. Менх (1939), В. Мейсснер (1941), М. Колер (1941, 1942) [85]. Одним из первых, кто использовал соотношение Онсагера для детального рассмотрения термоэлектрических явлений, был Л. Э. Гуревич (1940) [31].
Применению термодинамики необратимых процессов для описания термоэлектрических явлений были посвящены также работы Г. Каллена (1948), Р. Толмена и П. Файна (1948), Ж. Вершафельта (1950, 1951), Ч. Доменикали (1953, 1954) и др. [30, 39, 85,115,120]. Рассмотрение термоэлектричества в рамках дальнейшего развития термодинамики Онсагера осуществлялось И. Пригожиным (1947) и С. де Гроотом (1951) [75, 30],
Сравнение результатов расчета термоэлектрических величин на основе термодинамики необратимых процессов и кинетической теории провел Дж. Лич (1959) [146]. Исследование термоэлектрических явлений методами классической термодинамики и термодинамики необратимых процессов, сравнительный анализ полученных результатов выполнили Р. Хейкес и Р. Юр (1961) [133].
Детальная трактовка термоэлектрических явлений на основе термодинамической теории необратимых процессов представлена в монографиях известных советских физиков А. Г. Самойдовича «Термодинамика и статистическая физика», Л. Д. Ландау и Е. М. Лифшица «Электродинамика сплошных сред» [77, 60]. Результаты, полученные ими, и в настоящее время, не утратили своей актуальности благодаря простоте выбранных исходных уравнений и используемого математического аппарата.
(2.13)
Применив соотношения Онсагера к процессам распространения потоков тепла и электричества, А. Г. Самойлович для термоэлектрических, термомагнитных и гальванотермомагнитных явлений [6] вывел следующие основные формулы: 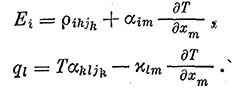
Здесь Ei = — νμ — компонент напряженности электрического по
ля; pik — компонент тензора удельного электросопротивления; аki, aim — компоненты тензора термо-ЭДС; qi, jk — компоненты вектора плотности теплового и электрического потока соответственно; Xlm — компонент тензора теплопроводности; μ — электрохимический потенциал носителей тока; е — их заряд; хт декартовы координаты. Индексы ί, к, I, т пробегают значения 1, 2, 3, причем по дважды встречающимся индексам ведется суммирование.
Принцип Онсагера приводит к следующим свойствам тензора р, κ, а и о:
 (2.14)
(2.14)
(Здесь В — вектор магнитной индукции; Пт — компоненты тензора коэффициента Пельтье.)
Структуру тензоров κ, р и а при В = 0 для кристаллов всех классов в середине 60-х годов определил Дж. Най [64].
Термодинамическая теория термоэлектричества совершенствуется по мере развития термодинамики необратимых процессов, введения в ее арсенал новых методов и представлений, позволяющих расширить задачи и возможности термодинамики как методологической основы естествознания и техники. В настоящее время неравновесная термодинамика сформировалась в отдельное научное направление со своими принципами, математическим формализмом и кругом проблем. Развитие общей теории неравновесных систем, анализ реакции линейной системы на внешнее возмущение, создание специальных методов решения конкретных вопросов неравновесной статистической механики и термодинамики необратимых процессов — все это представляет новые возможности для углубления как феноменологической, так и микроскопической теории термоэлектричества.
Так, создание в конце 50—начале 60-х годов метода термодинамических квантовых функций Грина, представляющего синтез некоторых идей статистической физики и квантовой теории поля, легло в основу квантовой теории кинетических коэффициентов К. Баумана (1963), который рассмотрел систему взаимодействующих электронов и фононов с учетом рассеяния электронов на хаотически распределенных примесях и электрон-электронного взаимодействия [101]. Теоретический анализ термоэлектрических явлений в примесной зоне с использованием функций Грина для разупорядоченных систем и упрощенной модели сильнолегированных полупроводников представили в 1972 г. X. Ван Конг и Г. Меснард [185].
Р. Кубо, осуществивший квантовомеханический подход к изучению неравновесных процессов, разработал метод получения точных формул для кинетических коэффициентов (в том числе и термоэлектрических) на основе гипотезы Онсагера, согласно которой релаксация случайной флуктуации микроскопической величине протекает в среднем в соответствии с макроскопическими физическими законами [24, 59]. Метод Кубо для вычисления термо-ЭДС-поляронов малого радиуса использовал в 1966 г. К. Шоттке [170]. На основе этого метода румынский физик Л. Георгеску рассчитал термо-ЭДС фононного увлечения в полупроводниках (1971) [130].
В 1962 г. П. Риссельберг предложил ввести в формализм необратимой термодинамики константы пропорциональности из линейных законов для обеспечения постоянства феноменологических коэффициентов системы при изменении локальных параметров. Возможность применения условия Риссельберга для описания термоэлектрических явлений доказали теоретически и экспериментально индийские физики М. Такур, М. Сах, К. Джа и М. Закариа в серии работ 1976—1978 годов [177].
Введение в термодинамическую теорию термоэлектричества принципа Кюри, согласно которому в изотропной среде тензоры различного тензорного порядка не взаимодействуют друг с другом, осуществили в 1980 г. О. Арнас и Д. Миллер [96].
Значительная роль в теории термоэлектричества принадлежит вариационному методу в его термодинамической формулировке, впервые использованному для решения кинетических уравнений М. Колером (1948, 1949) и развитому в работах Э. Сондхеймера (1950,. 1956), Дж. Займана (1956), X. Накано (1967) [40, 45, 158, 172].
Важным аспектом термодинамической теории термоэлектричества является ее применение к исследованию эффективности термоэлектрического преобразования энергии и расчету конкретных термоэлектрических устройств и установок. Такой подход, реализованный в теории полупроводниковых термоэлементов А. Ф. Иоффе (1949), является научной и методологической основой всех практических направлений термоэлектричества, сформированных к настоящему времени. Кроме того, этот путь играет существенную роль в определении перспектив термоэлектрического метода, в составлении прогноза его дальнейшего развития. Примером этого может служить· теоретический анализ термоэлектрического преобразования энергии, проведенный Э. Шмидтом (1967). Использовав термодинамические соотношения, он доказал, что КПД термоэлектрического генератора на базе полупроводниковых термоэлементов может достичь 20 % [169]. Последние Достижения в области термоэлектрического материаловедения [84, 94] подтвердили справедливость этого прогноза.
Представляет интерес изучение практических возможностей процесса, в котором энергия флуктуаций от средней энергии системы преобразуется в полезный вид энергии или используется в цикле охлаждения. Как известно, при работе современных электронных схем полупроводниковых приборов и других устройств происходят большие потери тепловой и электрической энергии, поэтому постановка такого рода исследований является перспективной для повышения эффективности приборов электронной техники, создания нового класса термоэлектрических преобразователей, так называемых воспроизводимых цепей с более высоким КПД, чем у традиционных. установок, изготовленных из тех же материалов. О первых результатах термодинамического обоснования такого подхода к термоэлектрическим процессам сообщалось на 2-й Международной конференции по термоэлектрическому преобразованию энергии (Арлингтон, США, 1978) [190].
В успешном развитии термодинамической теории термоэлектричества не менее важную роль, чем разработка фундаментальных представлений этой области, играет расширение круга явлений, которые можно описать феноменологическими уравнениями. В рамках этого подхода можно объяснить вопросы, ранее рассматриваемые только с точки зрения микроскопической теории (термоэлектрические эффекты в металлах, полупроводниках, электролитах, сверхпроводниках). Таким образом, термодинамическая теория термоэлектричества вносит существенный вклад в теорию кинетических явлений, физику твердого и жидкого состояний. Иллюстрацией может служить приложение термодинамики необратимых процессов к изучению термоэлектрических свойств полупроводников. Первыми работами в этой области были работы П. Клеменса по вычислению фононной составляющей коэффициента Томсона, Дж. Паррота по определению влияния теплового потока на коэффициент термо-ЭДС [138, 163]. П. Прайс (1956) показал, что применение принципа Онсагера позволяет получить связь между двумя феноменологическими параметрами явлений переноса, один из которых представляет отношение коэффициента термодиффузии к подвижности носителей, другой определяет тепловую энергию носителей, вызванную электрическим полем тока. Это соотношение использовалось при расчете термо-ЭДС [166].
Э. Хага (1959) в своей термодинамической теории двухзонных полупроводников вывел выражение для термо-ЭДС с учетом зависимости ширины запрещенной зоны от температуры. Аналогичную работу провел известный чешский физик Я. Тауц, однако он опроверг результаты, которые получил Хага, и показал, что температурная зависимость ширины запрещенной зоны не влияет на величину коэффициента термо-ЭДС [175].
Из последних исследований термоэлектрических явлений в полупроводниках на основе термодинамического подхода можно упомянуть работу Д. Райдена (1971) по сравнению свойств переноса в моно-, поликристаллических и порошковых анизотропных полупроводниках. Она дала возможность правильно оценить величины термо-ЭДС для различных структур одного из наиболее распространенных термоэлектрических материалов — теллурида висмута и его сплавов [168].
Использование соотношений термодинамики необратимых процессов в физике полупроводников в настоящее время уже можно считать классическим методом. На этой основе раскрыт материал таких известных монографий, как «Квантовая теория явлений электронного переноса в кристаллических полупроводниках» П. С. Зырянова и М. И. Клингера и «Физика полупроводников» К. Зеегера [50, 47].
Применение феноменологической теории позволило реализовать обобщенный подход к описанию процессов термоэлектрического преобразования энергии. На основе изучения обобщенной модели термоэлемента Л. И. Анатычук провел классификацию сред и воздействий (полей), приводящих к термоэлектрическому преобразованию энергии (табл. 2. 1) [5, 6]. Из таблицы видно, что существует 124 комбинации свойств сред и внешних воздействий, при которых может иметь место термоэлектрическое преобразование. Как следует из нее, в настоящее время исследуется только 18 вариантов термоэлектрических эффектов, пять из которых нашли практическое применение. Перспективы термоэлектрического метода преобразования во многом будут определяться дальнейшим изучением традиционных термоэлектрических эффектов и постановкой исследований термоэлектричества в сложных средах при воздействии на вещество комплекса факторов.
С помощью представлений о вихревом характере термоэлектрического поля были сформулированы условия для возникновения термоэлектрического тока

Первое слагаемое в левой части выражения соответствует вихревому термоэлектрическому полю, обусловленному анизотропией термо- ЭДС, второе — обусловлено неоднородностью коэффициента термо- ЭДС, третье — анизотропией коэффициента Томсона. Следовательно, для возникновения вихревого термоэлектрического тока и осуществления термоэлектрического преобразования необходимо, чтобы термоэлектрическая среда обладала либо неоднородностью, либо анизотропией термоэлектрических свойств. Кроме того, условие (2.15) указывает на возможность разделения на два класса любых распределений температур в среде: активные температурные поля, которые удовлетворяют условию (2.15) и описываются функциями Та (г), и пассивные температурные поля, для которых функции Тр (r) представляют решения системы уравнений RiTp(г) = 0. Таким образом, анализ общего условия (2.15) показывает, что в однородной изотропной среде вихревые термоэлектрические токи не возникают и термоэлектрическое преобразование энергии невозможно вследствие пассивности распределения температур в таких средах. Однако однородную изотропную среду можно преобразовать в среду с анизотропной или неоднородной термо-ЭДС, если подвергнуть ее внешнему воздействию, например, деформирующему усилию, магнитному полю, звуковому потоку и пр. Этот вывод теории подтвержден рядом экспериментов.
Таблица 2.1. Термоэлектрические среды и внешние воздействия, приводящие

Примечание. О — преобразование невозможно; + — исследуется; * — используется; ΔТ — одноосная деформация; В — электрическое ноле; V'T — условия большого градиента температуры; и анизотропные электропроводность и термо-ЭДС; σ (ж, у, z), а (ж, у, z) — неоднородные и изотропные электропроводность и термо-ЭДС воздействие, приводящее к перепаду
температуры в среде; Н — магнитное поле; Р — а, а — однородные и изотропные электропроводность и термо-ЭДС; σ— однородные изотропные электропроводность и термо-ЭДС; σ (x, у, z), а (x, у, z) — неоднородные.
В частности, в работе [8] представлены сведения об измерении вихревого термоэлектрического тока, возникающего в рамке из монокристаллического германия при ее деформации, причем значение тока соответствовало теоретически вычисленному по порядку величины и температурной зависимости.
Вихревые токи в однородной изотропной среде, помещенной в магнитное поле, описаны Л. Э. Гуревичем и Е. Ф. Шейдером (1969). В этом случае активными являются такие распределения температур, при которых градиент температуры по направлению отличен от вектора напряженности магнитного поля. К аналогичным качественным результатам, как показали эти исследователи, приводит замена магнитного поля потоком звуковых волн [6, 35].
Деформационный термомагнитный эффект, обусловленный вихревыми термоэлектрическими токами, рассмотрен Н. В. Заварицким и В. В. Лебедевым [44, 61].
В однородной среде, характеризующейся анизотропной термо-ЭДС, активные тепловые поля определяются градиентом температуры, не совпадающим по направлению с главными кристаллографическими осями. Таким образом, в данной среде существуют условия для возникновения вихревого термоэлектрического тока. Возникновение последнего в изотропной неоднородной среде возможно в том случае, когда градиент температуры не совпадает с направлением изменения коэффициента термо-ЭДС.
К преобразованию тепловой энергии в электрическую (6)

В зонально-неоднородной двухслойной среде, характеризуемой разрывом коэффициента термо-ЭДС, вихревой термоэлектрический ток создается, когда направление температурного градиента отличается от направления нормали к поверхности разрыва. Как показал А. Хиросэ [91], важным следствием изучения этого вопроса в изотропной среде явилась демонстрация зонально-неоднородной двухслойной среде, характеризуемой разрывом коэффициента термо-ЭДС, вихревой термоэлектрический ток создается, когда направление температурного градиента отличается от направления нормали к поверхности разрыва. Как показал А. Хиросэ [91], важным следствием изучения этого вопроса в изотропной среде явилась возможности использования вихревых термоэлектрических токов для определения толщины слоев, сопротивления биметаллических лент и пластин, а также термопар с гальваническим покрытием. Вихревые токи в тонких пленках изучали Н. В. Коломоец, Э. М. Скок, М. Д. Блох и др. [15, 55].
Условия, сформулированные в выражении (2.15), позволяют с единой позиции описать известные типы термоэлементов и изыскать новые нетрадиционные конструктивные варианты термоэлектрических преобразователей. Для каждого из известных вариантов термоэлементов можно представить соответствующую определенную картину вихревых токов в анизотропной и неоднородной среде. В то же время любой картине вихревого термоэлектрического тока можно поставить в соответствие определенный тип термоэлемента.
Векторные поля вихревых термоэлектрических токов в анизотропных и неоднородных средах отличаются большим разнообразием, что порождает множество вариантов термоэлементов и позволяет определить пути их оптимального конструирования.
Обобщенный подход к описанию термоэлектрических преобразователей позволил установить широкие возможности термоэлектричества и создать методологию разработки принципиально новых типов термоэлементов [6]. Для их оптимизации Л. П. Булатом и О. Я. Лусте введено понятие производящей функции [18].

