Расчет магнитной цепи должен включать в себя учет ферромагнитных участков, образованных сердечниками статора и ротора.
Во всех машинах переменного тока обмотка якоря укладывается в пазы. В неявнополюсных синхронных машинах и асинхронных машинах ротор также имеет зубчатое исполнение. Поэтому учет зубцовой зоны является одним из необходимых элементов магнитного расчета.
Зубцы машин переменного тока в большинстве случаев имеют форму равнобокой трапеции. Параллельно зубцам расположены пазы, по которым также частично проходит магнитный поток.
Пазы снабжены специальными гнездами, обращенными к расточке для установки пазовых клиньев, удерживающих обмотку. При магнитном расчете зубцов ослабление сечения зубца, связанное с установкой клиньев, обычно не учитывают.
При расчете общепринято делать следующие допущения: линии равного магнитного потенциала в зубцах и пазах представляют собой окружности с центром на оси машины.
Ввиду нелинейной зависимости В от Н при магнитном расчете зубцов и сделанных допущениях относительно распределения поля наибольшее практическое распространение получили численные методы интегрирования.
Разбивая зубец на большое число участков, расположенных, между линиями одинакового уровня, можно достигнуть большой точности при расчетах. Трудоемкость такого метода при ручном счете ограничивает его применение.
Поэтому нашли применение упрощенные методы расчета с помощью формул, которые в некотором диапазоне индукций и различных свойств магнитных материалов могут обеспечить практическую точность. В общем случае применимость таких формул проверяется методом численного интегрирования.
Обычно различают две зоны индукции при расчете н. с. зубцов. При индукции, меньшей 1,7—1,8 тл, отсос потока в паз незначителен, и здесь расчет ведется только по сечению зубца. Когда расчетная индукция в зубцах превышает 1,7—1,8 тл, вследствие сильного насыщения часть потока проникает в паз и это обстоятельство должно учитываться при расчете н. с. зубцов.
Если бы пазы и зубцы имели параллельные стенки (при бесконечно большом радиусе расточки), сечение паза и зубца по всей высоте сохранялось бы постоянным. В этом случае индукция в зубце и пазу сохранялась бы постоянной по всей высоте.
Расчет при Вz<1,8 mл сводился бы к определению Нz по Вz (по таблице или кривой намагничивания), и магнитное падение напряжения в зубце составляло бы (3-24а)
При высоких индукциях происходит частичное ответвление потока в паз и некоторая разгрузка зубцов. При ответвлении потока в паз можно записать:
(3-25)
где Фz — поток на зубцовый шаг; Фдz — действительный поток в зубце; Фп — продольный поток в пазу.
Определение индукции произведем делением (3-25) на ширину зубца bг и эффективную длину сердечника lе, тогда
(3-26)
где Вz — расчетная индукция в зубце; Вдz — действительная индукция в зубце; Нz— напряженность магнитного поля, соответствующая Вдz/kгz = bп/bz— коэффициент ответвления потока в паз; bп — ширина паза.
Построение кривой намагничивания материала с учетом отсоса части потока в паз при постоянном значении k2 не представляет особого труда. Задаются значением Вдz и по кривой намагничивания определяют напряженность Нz, затем по (3-26) находят Вz для заданного kz. Такие кривые Hz=f (Вz, kz) нашли широкое распространение при магнитном расчете зубцов.
Расчет зубцов в большинстве практических случаев усложняется тем, что сечение зубца (или паза) не остается постоянным по высоте. В этом случае значение индукции по высоте зубца будет переменным.
В практике получили распространение упрощенные приближенные формулы расчета по одному сечению, обычно на одну треть высоты зубца, считая от узкого основания, или по трем сечениям (в двух основаниях и посередине зубца).
Рис. 3-20. Кривые намагничивания клиновидного тела с учетом ответвления потока в паз для стали 341, 342, 343
(B0=0,4 mл)
При учете насыщения картина распределения магнитного поля по ярму сердечника изменяется в сравнении с тем, что было получено при постоянном значении и. Насыщение сердечника приводит к выравниванию распределения индукции по сечению ярма. В этом случае тангенциальная составляющая индукции на нейтрали становится почти постоянной.
Для определения н. с., необходимой для проведения потока, следует произвести интегрирование вдоль любой силовой линии магнитного поля. При учете насыщения н. с. ярма статора может быть также определена по формуле (3-44). Однако в этом случае коэффициент ка должен учитывать распределение индукции с учетом насыщения.
Коэффициент ka зависит как от геометрии ярма статора, числа полюсов, так и от степени насыщения. Он может быть определен экспериментально на моделях или с помощью построения картины поля с учетом насыщения. В 13-11 получена зависимость коэффициента ка от отношения высоты спинки к полюсному делению и от среднего значения индукции на нейтрали между полюсами. Кривые рис. 3-25 получены при синусоидальном распределении поля в воздушном зазоре.
В некоторых случаях расчеты производятся по формуле вида Fа1 = H'la, где Н'а—расчетная напряженность магнитного поля, соответствующая средней магнитной индукции В; lа — расчетная длина силовой линии ярма статора.
В этом случае расчетная напряженность магнитного поля Н'а приводится в таблицах в зависимости от индукции. Такие таблицы, например, приведены в гл. 9, в которой рассмотрен пример расчета магнитной цепи синхронной явнополюсной машины.
Рис. 3-25. Поправочный коэффициент ka для определения н. с. в ярме сердечника из высоколегированной электротехнической стали с учетом насыщения при синусоидальном распределении потока для двухполюсной машины.
Для многополюсных машин характерным является относительно слабое магнитное насыщение ротора. У явнополюсных машин обычно можно пренебрегать магнитным падением напряжения вдоль ярма ротора, поскольку высота спинки ротора в основном определяется механическими напряжениями. Для турбогенераторов и турбодвигателей, у которых число полюсов два или четыре, индукция в ярме ротора может достигать достаточно большой величины. В этом случае должно учитываться падение магнитного потенциала в ярме ротора.
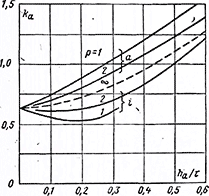
Рис. 3-24. Поправочный коэффициент ка для определения н. с. в ярме сердечника ненасыщенной машины
а — внешнее ярмо, ί — внутреннее ярмо, ∞— ярмо бесконечного радиуса
Если для неявнополюсных машин типа турбогенераторов ротор выполнен без центрального отверстия, то индукция на нейтрали между полюсами может быть определена по формуле:
(3-45)
где D2z — диаметр по дну пазов бочки ротора, см; l2—длина бочки ротора, см.
При таком написании учитывается проникновение части потока из бочки ротора в хвостовины.
Поскольку для двухполюсных турбогенераторов индукция во всех точках ярма одинакова, то н. с. для ротора двухполюсного турбогенератора без центрального отверстия может быть определена но формуле:
(3-46)
причем напряженность магнитного поля Ha2 соответствует индукции (3-45).
При наличии центрального отверстия диаметром D0 индукция на нейтрали между полюсами может определяться формулой:
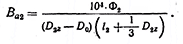, (3-47)
Очевидно, что в этом случае необходимо введение поправочного коэффициента на неравномерность распределения магнитной индукции по ярму ротора.
Для двухполюсного ротора н. с. может быть рассчитана по формуле:
где На2—напряженность магнитного поля, определяемая по индукции (3-47); ka2 — поправочный коэффициент для учета насыщения и неравномерного распределения индукции.
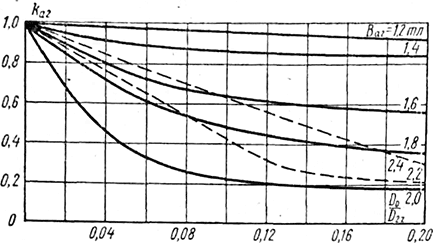
Рис. 3-26. Поправочный коэффициент ka2 к расчету н. с. ярма ротора с центральным отверстием
Значение поправочного коэффициента ka2 для роторных сталей приведено на рис. 3-26 [2-10].
Выражение (3-46) может
быть также использовано при
расчете машин с числом полюсов больше двух. Расчетная длина в этом случае может быть записана как
Однако при 2p> 2 значение индукции в ярме ротора обычно значительно меньше, чем у двухполюсных машин, и поэтому поправочный коэффициент насыщения можно не учитывать.
