Для расчета магнитной цепи необходимо предварительно рассчитать потоки рассеяния обмоток возбуждения, которые также будут нагружать магнитную цепь.
Потоки рассеяния сцеплены с обмоткой возбуждения и в основном проходят по воздушным промежуткам: поперек пазов или в промежутке между полюсами. Поэтому для расчета этих потоков сопротивление ферромагнитных участков цепи, по которым проходят потоки рассеяния, не учитывается.
Для неявнополюсных синхронных генераторов характерным является поперечно-пазовый поток рассеяния, поскольку обмотка возбуждения укладывается в радиальные пазы. Этот поток рассеяния проходит поперек зубцов и пазов и нагружает в продольном направлении большой зубец и ярмо ротора. При этом в нагружении ярма участвует весь поток рассеяния; большой же зубец в основании нагружается полностью потоком рассеяния, который затем ответвляется по высоте зубца в пазы.
Расчет потока рассеяния для этого случая может быть произведен по рис. 3-14. Элементарный поток на единицу длины ротора можно представить как![]()
После интегрирования получим

где
— магнитная проводимость для поперечно-пазового рассеяния прямоугольного паза; l2 — длина бочки ротора, см; F2'—н. с. ротора на один полюс; z2—число обмотанных пазов ротора и р—число пар полюсов.
Наиболее мощные турбогенераторы изготовляются с трапецеидальными пазами возбуждения. В этом случае может быть получена существенная экономия в потерях на возбуждения и облегчено охлаждение обмотки.
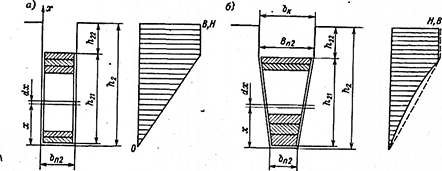
Рис. 3-14. К расчету рассеяния обмотки возбуждения с прямоугольным пазом (а)
и трапецеидальным пазом (б)
Выражение для проводимости пазового рассеяния приобретает вид
![]()
Функция ф (bn2/Вn2) представлена на рис. 3-15.
При расчете рассеяния по (3-23) и аналогичным формулам F2 представляет собой полную н. с. обмотки возбуждения за вычетом магнитного падения напряжения в самом роторе. Следовательно, F2 теоретически может быть получено, если н. с. возбуждения определяется по внешней характеристике и реакции якоря машины. Внешняя магнитная характеристика определяется магнитным сопротивлением, внешним по отношению к ротору, т. е. магнитным сопротивлением воздушного зазора, зубцовой зоны и ярма статора. Для определения F2 в формуле (3-23) необходимо построить диаграмму н. с. машины под нагрузкой с использованием вместо характеристики холостого хода внешней характеристики магнитной цепи. Такое построение показано на рис. 3-16.
Рассеяние полюсов явнополюсных синхронных машин может быть определено по картине поля, как это показано на рис. 3-5. Если силовые линии и линии уровня начерчены с соблюдением «квадратности» каждой клетки, то отношение потока рассеяния к основному потоку может быть определено как отношение числа силовых трубок, выходящих из полюсного башмака и сердечника-полюса, к числу силовых трубок, входящих в сердечник статора.
В результате построения многих картин поля могут быть получены приближенные формулы для определения коэффициентов рассеяния полюсов. Такие выражения приведены, например, в гл. 9 при расчете характеристики холостого хода явнополюсных, машин.
Аналогично может быть учтено рассеяние в торцевой части машин и лобовой части обмоток.
Поток в воздушном зазоре, конечно, не является чисто синусоидальным как для неявнополюсных, так и для явнополюсных машин. Определение действительной формы поля в воздушном зазоре является необходимым для расчета магнитной цепи.

Рис. 3-16. Диаграмма для определения н. с. F2 под нагрузкой
1 — характеристика холостого хода. 2 — переходная характеристика (падение магнитного напряжения в воздушном зазоре и сердечнике статора)
При определении н. с. воздушного зазора для явнополюсных синхронных машин было уже указано (§ 3-2) на способ определения коэффициента формы kф.
![]()

Рис. 3-15. Поправочный коэффициент φ для расчета проводимости рассеяния трапецеидального паза ротора
Принимая в первом приближении для неявнополюсных машин чисто трапецеидальное распределение индукции в воздушном зазоре, получим зависимость между амплитудой индукции основной гармонической Вδ1 и индукцией под большим зубцом Вδ:

где γ= z2/z0— отношение числа обмотанных пазов к числу пазовых делений; поправочный коэффициент для определения Βδ по первой гармонической принимает значения:
Он незначительно отличается от единицы, и поэтому для турбогенераторов во многих случаях расчет может быть сделан по первой гармонической индукции в зазоре.

