ГЛАВА ДЕСЯТАЯ
ОПТИМИЗАЦИЯ ПРОЕКТА. ПРОЕКТИРОВАНИЕ С ПОМОЩЬЮ ЭВМ
10-1. ОБЩИЕ ПОЛОЖЕНИЯ
Хотя оптимизация проектов может быть осуществлена и без помощи ЭВМ, более того, она так и производится в большинстве случаев, применение ЭВМ облегчает выполнение этой задачи и позволяет уточнять математические модели оптимального проектирования.
В настоящей главе основное внимание уделено общим вопросам алгоритмов получения оптимального решения. Таким решением называется набор значений независимых переменных, доставляющий экстремум некоторому функционалу, называемому целевой функцией или критерием оптимизации. Независимыми переменными могут быть размеры и прочие конструктивные данные, целевой функцией — масса, к. п. д., стоимость и т. п. Ряд величин — температура, транспортные габариты и т. д. выступает в качестве ограничений.
Решение задач такого рода рассматривается в развившихся за последние годы разделах математики, таких как исследование операций и математическое программирование; причем если целевая функция и система ограничений представляют собой линейные формы относительно независимых переменных, задача может быть решена хорошо разработанными методами линейного программирования. Реальные задачи проектирования электрических машин нелинейны, и общих методов решения таких задач в настоящее время не разработано.
Геометрически можно следующим образом интерпретировать решение оптимальной задачи: на некотором множестве переменных задано п координат и определена функция п координат, а также система т ограничений, определяющая в n-мерном пространстве многогранник, ограниченный т — 1 гиперповерхностями. В простейшем случае двух переменных z (x, у) имеет вид поверхности, показанной на рис. 10-1. В общем случае функция может не иметь максимумов и минимумов или иметь их несколько. В первом случае наибольшее или наименьшее значение будет находиться на одной из границ, во втором — в области изменения переменных. Решение, не доставляющее экстремума, но удовлетворяющее ограничениям, назовем приемлемым: оптимальным может быть одно из приемлемых решений, причем нас интересует общий, так называемый глобальный экстремум.
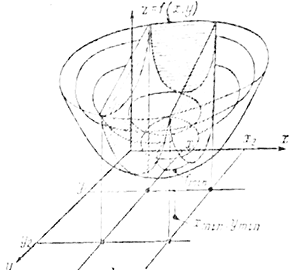
Рис. 10-1. Геометрическая интерпретация оптимизационной задачи для мучая двух переменных
Необходимо также отметить, что математическая модель, на которой решается задача оптимального проектирования, отражает свойства реальной машины лишь приближенно и ее составление требует конкретного подхода к каждой задаче. Отметим также, что такие критерии оптимизации, как минимум массы при заданном к. п. д. или максимум к. п. д. при ограничении массы, нс вызывают сомнений, однако на практике применяются более сложные критерии, например приведенная стоимость, хотя математически строгая оптимизация возможна только по одному критерию. Если в качестве критерия предлагаются две независимые оценки, то одна должна быть целевой функцией, а другая — ограничением. В случае сложного критерия, например приведенной стоимости, его элементы должны быть не независимы, а связаны экономическими или физическими законами, например, с помощью достаточно обоснованного срока окупаемости. В противном случае правильнее дополнить систему ограничений, нежели усложнять целевую функцию.
Существует ряд общих методов решения оптимальных задач, некоторые из них описаны ниже. Самый простой метод поиска экстремума — это перебор значений переменных на сетке с постоянным шагом; при большом количестве переменных п число расчетов тп, где т — число узлов сетки, возрастает настолько, что задача становится практически неразрешимой. Метод шагового поиска, при котором движение по сетке происходит только в направлении убывания или возрастания целевой функции, снижает число расчетов до 2п2т, однако при большом количестве переменных также не дает практического решения задачи. В связи с этим в практике применяют наряду с более совершенными методами поиска экстремума — градиентными, релаксационными и их модификациями — также методы «случайного» поиска, идеи динамического программирования и теории игр, и в большинстве случаев схема поиска представляет собой объединение нескольких алгоритмов. Дело в том, что расчетчик-проектировщик, зачастую решающий задачу поиска экстремума успешнее ЭВМ, также пользуется интуитивно или сознательно какой-либо математической процедурой, чаще всего несколькими различными алгоритмами, для разных частей задачи. Естественно, что при формализации его действий можно получить ценный материал для алгоритмов поиска с помощью ЭВМ.
Поиск экстремума облегчается тем, что в практических случаях экстремум находится почти всегда на ограничениях, кроме того, функция вблизи экстремума достаточно полога, так что небольшая ошибка в определении экстремума не приводит к существенному изменению целевой функции и, что очень важно, что некоторые переменные вблизи экстремума слабо влияют на целевую функцию, что позволяет считать их приближенно постоянными. Кроме того, если функция может быть разбита на отдельные части, относительно слабо связанные между собой, то можно найти экстремум для каждого члена и применить релаксационную процедуру для поиска глобального экстремума, находя поочередно экстремум для каждой из подзадач.
Два последних обстоятельства представляются наиболее важными: на основе возможности приближенного отыскания экстремума по минимальному набору независимых переменных строятся все методы поиска приемлемых значений целевой функции в окрестностях оптимума. На основе разбиения оптимизационной задачи на ряд подзадач, решение которых находится различными методами, В. М. Зайчик разработал оригинальную схему проектирования асинхронных двигателей по минимуму приведенной стоимости.
10-3. МЕТОДЫ ОПТИМИЗАЦИИ. ПРИМЕНЯВШИЕСЯ ПРИ ПРОЕКТИРОВАНИИ СЕРИЙ ДВИГАТЕЛЕЙ А2 И А02 (10-1. 10-2).
При расчетах серии двигателей А2 и А02 был успешно применен метод обхода сетки (перебора) с помощью ЭВМ. При этом наряду с вычислительными возможностями ЭВМ использовались ее логические возможности. В качестве критерия оптимальности принимался минимум обобщенной (т. е. приведенной) стоимости двигателя Р.

Рис. 10-5. Структурная схема расчета двигателя по методу 110-2]
Структурная схема, приведенная в (10-2) (рис. 10-5), предусматривает варьирование четырех параметров: числа проводников s в пазу статора, индукции В6 в воздушном зазоре, диаметра росточки статора D и внешнего диаметра Da. Этими параметрами однозначно определяется и длина двигателя I.
В ЭВМ вводятся следующие исходные данные: напряжение, частота, число и сопряжение фаз, полезная мощность, число пар полюсов, число параллельных ветвей, шаг обмотки и обмоточный коэффициент статора, размер воздушного зазора, числа пазов статора и ротора, коэффициент заполнения паза статора, ширина шлица паза статора, уровни индукции
в спинке и зубцах статора, стоимостные данные, таблица диаметров изолированных проводов, полиномы для кривых намагничивания, другие справочные материалы и нормативы.
Для контроля пригодности испытуемых комбинаций в программе задаются пять показателей-лимитеров: 1) предельная кратность λ£ρ максимального момента; 2) предельная кратность k'i" пускового тока; 3) предельная кратность пускового момента; 4) предельная температура 0пр перегрева обмотки статора; 5) предельная скорость нарастания температуры обмотки статора Тпр.

Рис. 10-6. Обход сетки при поиске оптимального варианта 110-21
Задаются также исходные (наибольшие) и предельные (наименьшие) значения варьируемых параметров. Но этим данным программа формирует комбинации значений независимых переменных, которые должны подвергаться очередному испытанию.
Исходя из заданных уровней индукции в спинке и зубцах статора определяются размеры пазов, подсчитываются сечения изолированного паза и с учетом заданного коэффициента заполнения паза, выбирается по сортаменту диаметр обмоточного провода.
Форма и размеры пазов статора определяются с учетом пусковых характеристик (см. блок-схему рис. 10-5).
Комбинации формируются перебором Вδ и s при Dа = const и Dа = const.
Исходной узловой точкой является sисх), как показано на рис. 10-6.
В процессе расчета производится сплошной обход сетки (см. рис. 10-6). Для ускорения обхода программа предусматривает условия, при которых машина, обнаружив на данной вертикали «непригодные» точки, следующие за «пригодными», не доходит до точки sпр, а сразу переходит в точку sисх соседней вертикали.
Таким же образом осуществляется обход узловых точек сетки для каждого из остальных значений D,. Когда все значения пройдут испытания при Da= const, цикл расчетов возобновляется при новом значении Da.
При проектировании двигателей серий А2 и АО2 испытывались 6 значений D, и 6 значений Da (с шагом 2,5%), т. е. обход узловых точек сетки Вδ, s совершался 36 раз.
Из блок-схемы видно, что переход от испытуемой комбинации к следующей совершается не обязательно после завершения всего расчета (т. е. после определения стоимости Рr). Необходимость в полном расчете отпадает, если комбинация не удовлетворяет хотя бы одному из технических требований, определяемых показателями-лимитерами θпр, kпр, Тпр, что обнаруживается до определения стоимости Рr. Последняя подсчитывается только для тех комбинаций, которые удовлетворяют всем техническим требованиям. Если оказывается, что Рr больше наименьшего значения стоимости Pmin, найденного для ранее испытанных комбинаций, то очередная r-я комбинация отбрасывается. Если Рr < Рmin, то r-я комбинация запоминается и Р, становится Rmin.
Увеличение числа независимых переменных до 7 (10-35) требует вследствие резкого возрастания числа расчетов применения метода случайного поиска с самообучением, предложенного С. Е. Даниленко. Этот метод сводится к следующему.
В n-мерном пространстве отыскивается точка х с координатами, которые обращают в минимум функцию обобщенной стоимости F → min при s условиях, определяемых техническими требованиями и имеющих вид gk ≥0, k = 1, . . S, и при выполнении требования неотрицательности геометрических размеров и подкоренных выражений.
На начальном этапе испытываются случайные точки у, пока не будет найдена начальная точка х0, принадлежащая допустимой области.
Из точки x0 совершаются пробные перемещения 7. Если в результате некоторого заранее установленного числа пробных попыток удается отыскать в допустимой области такую точку х1, для которой F(x1)< F (x1), то x1 становится отправной точкой для следующих пробных перемещений. В противном случае шаг уменьшается, и поиск новой точки продолжается в окрестности точки х0.
По мере накопления информации ЭВМ вырабатывает предпочтительное направление движения. С этой целью машина запоминает т последних точек: xl, xl-1,. . . , xl-m+1 с соответствующими значениями функции F и вычисляет по полученным данным вектор 0 (xl). Последний вместе с вырабатываемым в машине случайным вектором λ определяет направление очередного пробного перемещения.
В том случае когда лучшую точку удается отыскать, не исчерпав установленного числа пробных попыток, шаг для последующих попыток увеличивается.
Поиск оптимального варианта при семи переменных требует в среднем около 100 пробных расчетов. Но в некоторых случаях возникают затруднения, которые могут намного удлинить поиск. Т. Г. Сорокер приводит трудный случай, когда потребовалось 112 пробных расчетов только при двух варьируемых параметрах.

