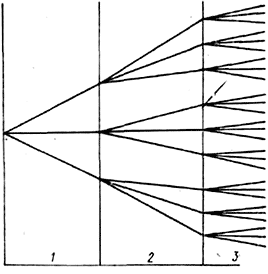
Рис. 10-14. Общая схема динамического программирования.
Общие положения.
В отличие от гидрогенераторов главные размеры асинхронных двигателей определяются чаще всего экономическими соображениями, вследствие чего задача их проектирования весьма трудоемка: в процессе проектирования должно быть определено около 20 независимых величин. На практике задача эта разбивается на ряд этапов: определение главных размеров, расчет обмоток, определение пазовой геометрии и т. д., на каждом этапе проектировщик принимает решения, допустимость которых проверяется на последующих этапах. Эта схема напоминает метод динамического программирования, позволяющий на каждом этапе выделить лучшее из всех возможных решение.
Действительно, если на этапе 1 (рис. 10-14) удалось найти лучшее из решений, то в дальнейшем все остальные могут уже не рассматриваться. На этапе 2 достаточно рассмотреть только те п решений, к которым приводит лучшее из решений, найденное на этапе 1. Аналогично на этапе 3 рассматриваются только те п решений, к которым приводит лучшее из решений, найденное на этапе 2, и т. д.
Всего должно быть рассмотрено пxт комбинаций вместо п при простом комбинаторном переборе. Например, при 10 этапах, каждый из которых допускает по три решения, достаточно рассмотреть 30 комбинаций вместо 310.
Однако вычислительная схема метода динамического программирования вызывает большие трудности при ее применении к задаче проектирования оптимальной электрической машины. Во-первых, требуемая в этом случае проверка на последующих этапах допустимости ранее принятых решений не укладывается в обычную вычислительную схему метода динамического программирования; во-вторых, вычислительный процесс осложняется тем, что на каждом из этапов варьированию подвергаются одновременно несколько переменных. Поэтому нам приходится отказаться от метода динамического программирования в его обычной или модифицированной форме.
При этом мы используем основную идею этого метода, согласно которой на каждом этапе выделяется наивыгоднейшее из возможных решений. Если нам удается разложить задачу на ряд подзадач и для каждой найти каким- либо способом экстремальное решение, то, так же как и в случае применения динамического программирования, станет возможным отбросить все остальные решения.
Как и в случае линейного программирования, будем стремиться формировать задачи — блоки — таким образом, чтобы их связи друг с другом были как можно слабее. Всесторонний анализ задачи проектирования показывает, однако, что не удастся осуществить разложение, при котором в разных подзадачах не участвовали бы общие переменные.
Но если нельзя полностью избежать участия в разных подзадачах общих переменных, то должны быть разработаны специальные приемы, которые обеспечили бы согласование решений этих подзадач, и притом таким образом, чтобы не допустить неоправданного возрастания функционала.
Способы, удовлетворяющие этим требованиям, описаны ниже. Они предполагают лишь небольшое число общих переменных в разных подзадачах и оказываются наиболее эффективными при малом числе испытуемых значений каждой из переменных. Последнему условию удовлетворяют такие переменные, которые либо могут принимать только дискретные значения, либо в связи с небольшим влиянием на величину функционала допускают испытания через достаточно крупные интервалы. Уже из одного этого можно заключить, что формирование подзадач не может быть осуществлено произвольным расчленением исходной задачи на любое число отдельных частей. Специальные исследования при формировании подзадач необходимы еще и по другим причинам.
Для каждой из выделенных подзадач должно оказаться возможным, во-первых, разработать математическую модель, во-вторых, найти способ получения оптимального решения. Если оказывается, что для какой-нибудь подзадачи эти требования не могут быть выполнены, то, очевидно, что выделение ее лишено смысла и, следовательно, разложение исходной задачи должно быть осуществлено иначе.
Иллюстрацией к утверждению, что подзадачи-блоки не могут формироваться произвольно, может служить тот факт, что ни один из сложившихся этапов традиционной схемы проектирования асинхронного двигателя не соответствует полностью указанным требованиям.
Обеспечение совместности решения разных подзадач, имеющих общие переменные.
Рассмотрим следующую ситуацию. Имеются две составные части приведенной стоимости,
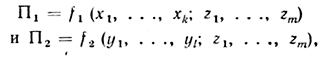
где переменные z1, . . ., zm одновременно влияют на величины П1 и П2.
Если для минимизации суммы П1 + П2 мы будем решать порознь две задачи, то значения переменных z1,.....zт. при которых Пх достигает минимума, могут расходиться со значениями этих переменных, минимизирующих П2. В том случае когда варьирование переменных zi вызывает большие изменения П2, и лишь незначительные изменения П2, минимум суммы П1+П2 будет, очевидно, достигнут при тех значениях zi, которые обращают в минимум величину П1 (хотя при этих значениях переменных величина П2 может оказаться больше своего возможного минимума). Но если при варьировании z, изменения величин П1 и П2 сравнимы, то для определения таких значений общих переменных, которые минимизируют сумму П1 + П2, должны быть разработаны специальные приемы.
Выше уже указывалось, что при формировании подзадач следует избегать случаев, когда число общих переменных в разных подзадачах велико. При соблюдении этого условия совместность решения подзадач с общими переменными может обеспечиваться одним из следующих способов:
а. Способ перебора. Если число общих переменных не превышает 1—2 и притом число значений, которое требуется рассмотреть для каждого из них, невелико, то, задаваясь последовательно этими значениями, можно получить спектр решений. Пусть, например, переменная z1 может принимать три различных значения z. Тогда получим соответственно минимальные значения
![]()
Сравнивая суммы![]()
можем непосредственно определить наименьшую из них и найти оптимальные из всех рассмотренных значений z1.
б. Способ взаимной увязки решений посредством последовательных приближений. Принципиальная особенность этого способа состоит в том, что при решении подзадач с общими переменными только часть из них рассматривается в отдельных подзадачах в качестве разрешающих (искомых).
Пусть в подзадачах № 1 и № 2 имеются общие переменные z1 z2 и z3. Примем, что в подзадаче № 1 разрешающими являются только z1 и z2, а в подзадаче № 2 — только z3.
Переменная zа будет участвовать в подзадаче № 1 в качестве «внешней», или экзогенной, т. е. ее значение, хотя бы и не наивыгоднейшее, должно быть известно до начала решения подзадачи № 1. Аналогично переменные z1 и z2, которые являются в подзадаче № 1 разрешающими, будут экзогенными по отношению к подзадаче № 2.
Схемы данного способа легко можно понять из следующего. Задавшись каким-нибудь значением z3, решаем подзадачу № 1. Найденные оптимальные значения z1 и z2 позволяют при решении подзадачи № 2 считать зги переменные экзогенными. Решив подзадачу № 2 и найдя оптимальное значение zя, используем его при повторном решении подзадачи № 1. Применяя этот принцип, повторяем процедуру решений двух экстремальных подзадач до тех нор, пока расхождения между двумя последовательными значениями соответствующих переменных не станут близкими к нулю.
Оптимизационный расчет асинхронного двигателя на ЭВМ с помощью метода разделения параметров
а. Постановка задачи. В качестве исходных данных рассматриваются: Р2—требуемая механическая мощность, вт; М мах максимальный момент, н-м; Мп— пусковой момент, н-м: (sд, Мд)— координаты точки, ниже которой механическая характеристика не должна проходить, в системе s (скольжение), М (момент); величины sд и Мд определяют жесткость механической характеристики; In1 — максимальное допустимое значение пускового тока, а; η— минимальный допустимый к. п. д., если он оговорен в тех условиях; 0доп—допустимое превышение температуры обмотки, град.
Ищутся также размеры и обмоточные данные машины, которые обеспечили бы ее максимальную экономичность при одновременном выполнении предъявляемых к ней эксплуатационных технических требований.
Из всех переменных по общепринятой методике выбираются следующие: число зубцов статора; число зубцов ротора; воздушный зазор δ, м; пазовые открытия; схема обмотки статора, а также число параллельных ветвей а и число элементарных проводников п в одном эффективном.
В качестве варьируемых переменных принимаются: D — диаметр расточки статора, м; I— расчетная длина пакета, м; kD— отношение наружного диаметра пакета статора к диаметру расточки; — отношение внутреннего диаметра пакета ротора к диаметру расточки; kпо — коэффициент пазовости статора (отношение суммарной площади пазов статора к площади, заключенной между двумя ограничительными окружностями листа статора); кпр—коэффициент пазовости ротора (отношение суммарной площади пазов ротора к площади, заключенной между двумя ограничительными окружностями роторного листа); w — число витков фазы.
Определение этих переменных описано в настоящем параграфе.
Кроме того, ниже приведен выбор геометрических размеров пазов статора и ротора из условия обеспечения минимума намагничивающего тока.
б. Сущность метода разделения параметров (метода предельных значений расчетной длины). Одновременное варьирование всех переменных обусловило бы практически невыполнимый объем расчетов. Кроме того, произвольное сочетание варьируемых величин приведет к рассмотрению большого количества заведомо непригодных вариантов. С целью упрощения вычислительной процедуры применим следующие приемы:
а. Сузим насколько возможно зону поиска, так чтобы не вводить в рассмотрение безнадежно плохие варианты. Для этого производится предварительная оценка возможных сочетаний w, D, kD (см. стр. 476).
б. Будем использовать поочередное изменение переменных D, kп.с, kn.р, предусматривающее постепенное улучшение плана с помощью метода последовательных приближений; указанное варьирование производится по приведенному ниже правилу поиска.
в. Правило поиска. Шаг 1. Варьируется диаметр расточки статора D. Каждое из испытуемых значений D является «кандидатом» на выход в оптимальное решение (Dкт)· Для этого Dкт отыскивается наивыгоднейшая расчетная длина-«кандидат» lкт. Из всех пар Dкт, lкт выбирается та, которой соответствует наименьшая (по сравнению с другими парами) приведенная стоимость. Диаметр D этой пары принимается оптимальным на данном шаге (D) и используется в качестве входной величины на двух последующих шагах. Еще раз подчеркнем, что kп.с и kп.р на этом шаге имеют фиксированные значения.
Шаг 2. Варьируется коэффициент пазовости статора kn.с. Каждое испытуемое значение kп.с рассматривается как «кандидат» на выход в оптимальное решение kп.с, и ему ставится в соответствие наиболее выгодная расчетная длина lкт. Путем сравнения приведенных стоимостей для всех пар kктпс, lкт находится наивыгоднейшее (на данном шаге) значение коэффициента пазовости, который принимается фиксированным на двух последующих шагах.
Шаг 3. Варьируется коэффициент пазовости ротора kn.р. Для каждого испытуемого значения находится наивыгоднейшая расчетная длина. Для пары вычисляется приведенная стоимость. В качестве принимается то значение, которому соответствует наименьшая величина приведенной стоимости. Величина kп.р принимается фиксированной на двух последующих шагах.
После выполнения шага 3 следует проделать очередной расчетный цикл, повторив шаги 1, 2, 3 при новых фиксированных значениях переменных. Процесс ведется до обеспечения сходимости, когда обнаруживается невозможность сколько-нибудь существенно снизить значение приведенной стоимости при изменении D, kn.c, kп.р.
Значения kп.с и kn.р, фиксируемые в начале первого итерационного цикла, можно выбрать из промежутков:
![]()
Отметим, что после первого шага в случае необходимости, производится корректировка величины kd, которая должна быть как можно меньше (но не в ущерб прочности или жесткости машины). Предварительно можно взять kd = 0,25:0,4.
Схематически правило поиска представлено на рис. 10-16.
Опишем кратко суть определения наивыгоднейшего значения расчетной длины lкт на каждом шаге процесса поиска (более подробно этот вопрос освещен ниже).
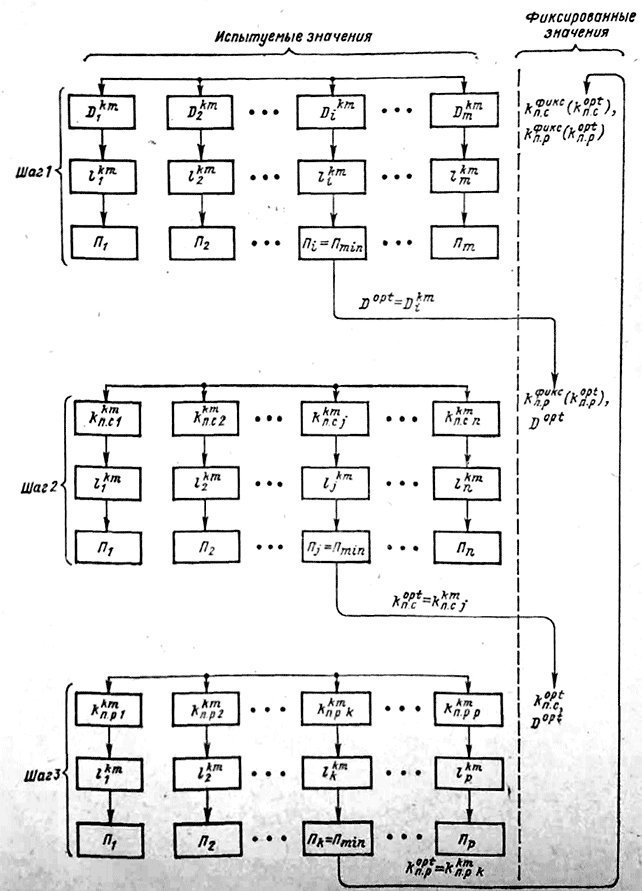
Рис. 10-16. Блок-схема алгоритма проектирования двигателя по минимуму приведенной стоимости.

