Коммутация коллекторных машин - Уравнения коммутируемого контура

Уравнения классической теории коммутации

Как известно, в основе уравнения коммутируемого контура классической теории сопротивление щеточного контакта принято неизменным, а точки контактирования равномерно распределенными по всей поверхности щетки. Уравнение тока секции, написанное для случая, когда э. д. с. самоиндукции es полностью уравновешивается посредством э. д. с. от поля коммутационной зоны ек и ширина щетки bщ соответствует коллекторному делению βκ, будет иметь следующий вид:

(1-1)

где Т—период коммутации.
На основе изложенного выше относительно поведения щеточного контакта при различных режимах его работы, казалось бы, можно было сделать 'вывод о полной несостоятельности написанного уравнения. Однако подобное заключение не будет полностью соответствовать истине. Исследования, проведенные на искусственных аппаратах, воспроизводящих коммутационный процесс, показывают, что прямолинейная коммутация, описываемая (1-1) и графически представленная на рис. 1-10 (линия 1), имеет место в том случае, когда плотность тока в контакте и его температура невелики, а состояние коллектора и щеток обеспечивает спокойную работу щеток в механическом отношении.
Но вместе с ростом температуры контакта его сопротивление начинает уменьшаться, а поэтому сопротивление секции Rc становится соизмеримым с сопротивлением щеточного контакта, в силу чего прямолинейная коммутация переходит в новую фазу, которая выражена уравнением (1-2):
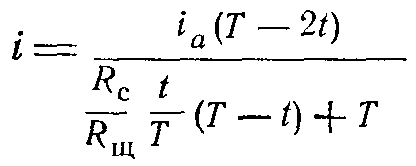(1-2),
а графически представлена кривой 2 на рис. 1-10.
В отличие от первой фазы коммутации, которой соответствует равномерное распределение тока в контакте.

Рис. 1-10. Кривые тока коммутируемой секции для случая, когда Rщ=const.

здесь работа контакта характеризуется смещением тока от средней части щетки к ее краям, благодаря чему условия работы сбегающего края щетки, выполняющего наиболее ответственный этап в коммутационном процессе, становятся значительно более тяжелыми.
Дальнейший же нагрев коллектора и щеток приводит кривую тока к виду, который не описывается ни одним уравнением классической теории коммутации, благодаря тому что условие Rщ=const уже не имеет места. Классическая теория коммутации при условии отсутствия полной компенсации, т. е. для случая, когда, дает уравнение для тока коммутируемой секции: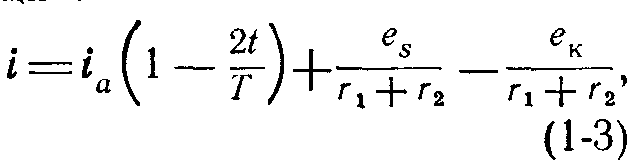
которое графически изображается кривыми 3 и 4 на рис. 1-10.
Автору, исследовавшему коммутационный процесс машин малой и средней мощности, никогда не приходилось наблюдать, чтобы опытные кривые замедленной и ускоренной коммутации хотя бы отдаленно напоминали соответствующие кривые классической теории коммутации. Однако не исключена возможность, что для машин большой мощности при недостаточно высокой температуре коллектора могут быть получены кривые, в какой-то мере сходные с приведенными на рис. 1-10, но они не будут характерными для современных электрических машин, работающих с большой плотностью тока в щеточном контакте и со значительной температурой коллектора и щеток.
Несоответствия классической теории реальным явлениям при коммутации заставили искать новые пути для решения вопроса о форме кривых тока и э. д. с. коммутируемого контура.

Уравнения О. Г. Вегнера

В 1938 г. О. Г. Вегнер [Л. 1-4] опубликовал работу, в которой рассмотрел коммутируемый контур не на основе ∆u=const, как это принято в классической теории, а с допущением постоянства падения напряжения в щеточном контакте. В свое время автор [Л. 1-5] по поводу теоретических положений О. Г. Вегнера отметил «...теория, в основу которой положено условие, ближе к истине, чем Rщ=const». Такого же мнения автор придерживался и в настоящее время, имея в виду, конечно, машины, работающие с достаточно высокой температурой коллектора и щеток.
На основеуравнение коммутируемого контура (рис. 1-1) принимает вид:

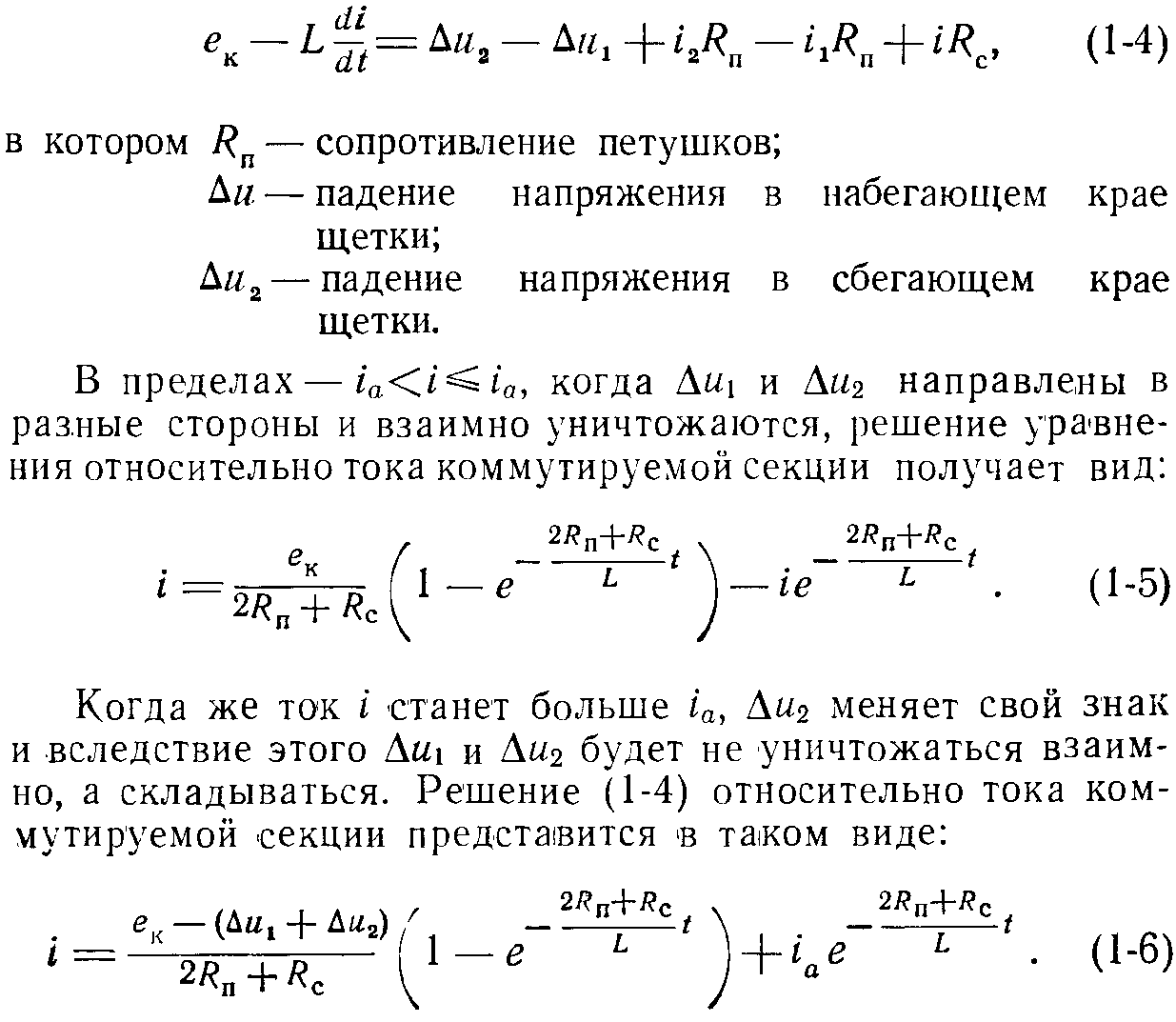
О. Г. Вегнер провел опытную проверку полученных уравнений, давшую достаточно удовлетворительную сходимость теоретических кривых с экспериментальными.

Уравнения И. С. Елохина

 Значительно позднее И. С. Елохин, учитывая ряд экспериментальных работ, принял, что сопротивления набегающего края щетки r1 и сбегающего r2 не изменяются плавно
в функции времени, а остаются почти в течение всего периода коммутации постоянными и не зависящими от поверхности соприкосновения щетки с коллекторной пластиной, т. е. r1 = r2 = const. Уравнение тока для данных условий при отсутствии э. д. с. ек напишется следующим образом:

Следует отметить, что положения, взятые И. С. Елохиным в основу при составлении дифференциального уравнения коммутируемого контура, были перенесены Ю. Е. Неболюбовым [Л. 1-8] на коммутируемый контур коллекторных двигателей переменного тока. Экспериментальная проверка полученных теоретических данных и в этом случае показала их удовлетворительную сходимость.
Автор считает, что в данный момент, когда нет еще исчерпывающих данных, на основе которых можно было установить степень достоверности формул, предложенных О. Г. Вегнером и И. С. Елохиным для различных условий коммутации, нет необходимости делать по этому вопросу какие-либо категорические заключения, тем более, что в последующих разделах будет показано, что характер кривой тока коммутируемой секции на первом этапе коммутации играет значительно меньшую роль, чем это казалось в недалеком прошлом, в особенности это относится к машинам с добавочными полюсами.

Уравнения Б. К. Тура и А. И. Скороспешкина

Следует отметить, что сравнительно недавно была сделана попытка рассмотреть уравнение коммутируемого контура посредством аппроксимации переходного сопротивления по вольт-амперной характеристике. Б. К. Тур [Л. 1-6] провел математические исследования коммутации для схемы замещения (рис. 1-11), причем решение полученного уравнения было проведено приближенным методом, на основе вольт- амперной характеристики щеточного контакта для малых значений токов, а для плотностей более 8 а/см² согласно уравнению .

Рис. 1-11. Схема коммутируемого контура, рассмотренная Б. К. Туром.

Что касается распределения тока в различных частях щетки, то оно принималось таким же, как и в классической теории. Выводы Б. К. Тура показывают, что к вопросу аппроксимации вольт-амперной характеристики в уравнении коммутируемого контура нужно подходить весьма осторожно. Вследствие того, что Б. К. Тур принял вольт-амперную характеристику в виде прямой с некоторым постоянным подъемом, вплоть до 8 080 а/cм² и получил падения напряжения в контакте, превышающие 200 в, что ни в какой мере не увязывается с опытными данными.
А. И. Скороспешкин [Л. 1-7] принял допущение, согласно которому сопротивление щеточного контакта уменьшается при возрастании плотности тока по закону прямой линии, и полученное на этой основе уравнение сопоставил с экспериментальными данными. Эта проверка показала также удовлетворительную сходимость теоретических и опытных кривых. А. И. Скороспешкин аппроксимировал сопротивление щеточного контакта в функции плотности тока также и кривыми экспоненциального и гиперболического вида, причем и в этом случае опытная проверка не показала больших отступлений от теоретических кривых.
Однако следует заметить, что А. И. Скороспешкин проводил опыты с весьма небольшими плотностями тока в щеточном контакте (3—4 а/см²) и при температуре коллектора не свыше 50° С, а поэтому выводы, сделанные им, не могут распространяться на современные электрические машины. Они могут найти некоторое применение лишь при конструировании электромашинных усилителей, в которых весьма часто плотности тока в контакте устанавливают очень небольшими.
Резюмируя результаты в области математических исследований кривых тока коммутируемого контура, следует еще раз подчеркнуть, что коммутационный процесс является в высшей степени сложным и многогранным. В нем из-за изменения форм электрической проводимости в щеточном контакте, зависящих от весьма большого количества факторов, происходят и соответствующие изменения в форме кривой тока коммутируемой секции, а поэтому ни одно уравнение, в котором не учитываются эти свойства контакта, не может рассматриваться как общее. Рассмотренные выше уравнения могут в той или иной степени соответствовать лишь отдельным условиям коммутации, а поэтому их практическое значение не следует преувеличивать.