4-3. РЕЗУЛЬТАТЫ ОПЫТНЫХ ИССЛЕДОВАНИЙ КРИВЫХ ТОКА И Э. Д. С. ПРИ КОММУТАЦИИ НА ИСКУССТВЕННЫХ АППАРАТАХ
Опыты О. Г. Вегнера
Результаты опытных исследований кривых тока и э. д. с. коммутируемого контура, проведенных на реальных машинах, здесь не рассматриваются, так как они уже позволили сделать достаточно четкий вывод, состоящий в том, что действительный период коммутации получается всегда меньше периода, соответствующего ширине щетки в тангенциальном направлении. Это было нами отмечено при рассмотрении методов осциллографирования кривых тока и э. д. с. коммутируемого контура реальных машин.
О. Г. Вегнер поставил опыты на описанной выше установке, воспроизводящей коммутацию, чтобы выяснить, насколько допущение постоянства сопротивления щеточного контакта, принятое в основу классической теории коммутации, соответствует действительному процессу в коммутируемом контуре. Одновременно с этим была поставлена задача проверить уравнение для тока коммутируемой секции, полученное на основе постоянства падения напряжения в контакте. Так как уравнение, полученное О. Г. Вегнером на основе ∆u=const, не описывает полного реверса тока от значения +ia до —ia, оно рассмотрено для случая, когда ек≠0.
На рис. 4-11 приведены как осциллограмма тока коммутируемой секции 2, так и расчетные кривые — по уравнению, в основе которого ∆u=const, 1 и уравнению классической теории коммутации с допущением Rщ=const 3 при ек=1,9 в и ία=10 а.
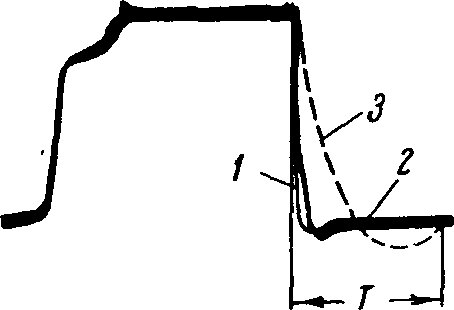
Рис. 4-11. Осциллограммы тока коммутируемой секции в сравнении с теоретическими кривыми, полученными на основе Rщ= const и Δu = const.
Судя по очертанию кривой 2, полученной экспериментально О. Г. Вегнером, есть основания думать, что опыт для ее снятия проводился при достаточно нагретом коллекторе, так как в противном случае результаты были бы больше в пользу уравнения классической теории. К сожалению, температурное состояние щеточного контакта при проведении опыта в статье не приводится. Но тем не менее из сопоставления приведенных кривых можно заключить с полной уверенностью, что очертание кривой тока коммутируемой секции по уравнению О. Г. Вегнера для условий опыта, имевших место при данной экспериментальной проверке, значительно ближе к истине, чем очертание кривой, полученной по уравнению классической теории коммутации.
Коммутацию, соответствующую расчетной кривой на рис. 4-11, О. Г. Вегнер рассматривает как «весьма интересный режим», способный обеспечить безыскровую коммутацию, применение которой, как он пишет, «позволит преодолеть серьезные трудности на пути сооружения мощных коллекторных машин». В дальнейшем этот режим работы щеточного контакта им назван «ступенью малого тока» и несколько более полно освещен [Л. 4-5]. На рис. 6-1,б приведена кривая тока коммутируемой секции с обеспечением ступени малого тока, которая соответствует щеткам, имеющим характеристику ∆u=const. В отличие от теоретической и опытной кривых экспоненциального вида (рис. 4-11) новая кривая тока, позволяющая, по мнению О. Г. Вегнера, решить проблему коммутации, изображается почему-то не в виде экспоненты, а в форме прямой, которая возможна только при условии, когда еи=еr и Rщ=const и соответствует прямолинейной коммутации классической теории.
Вопрос получения малого тока разрыва при завершении коммутации никогда не вызывал сомнений, ничего нового, открывающего большие возможности, о которых говорит О. Г. Вегнер, здесь нет. Значительно большее значение здесь имеют пути получения практически обесточенного контакта в сбегающем крае щетки к моменту завершения коммутации. Так, например, А. Б. Иоффе [Л. 4-6, 4-7], рассматривая коммутацию тяговых двигателей, подчеркивает, что наилучшей кривой тока в коммутируемой секции является кривая несколько ускоренной коммутации, характеризующаяся меньшей величиной di/dt в момент окончания коммутации. Ускоренная коммутация предпочиталась многими исследователями в этой области именно благодаря тому, что она к моменту покидания щеткой коллекторных пластин может обеспечить отсутствие тока в последних точках контакта между щеткой и коллектором при завершении коммутации.
Теория ступени малого тока базируется на характеристике, которая в области больших плотностей тока соответствует условию Au = const, а при малых должна соответствовать большим значениям du/dl при условии ∆u≈kj, что при теоретическом решении вопроса приведет к непреодолимым трудностям.
Как известно, попытки аппроксимировать статическую вольт-амперную характеристику в уравнении кривой тока коммутируемого контура имели место, однако несмотря на то, что аппроксимация была в высшей степени упрощенной, она приводила к уравнениям, теоретическое решение которых оказалось невозможным, поэтому подобного рода уравнения решали приближенными методами, а результаты их решения в силу грубой аппроксимации вольт-амперной характеристики оказались в резком противоречии с опытом. Вполне понятно, что теоретическое решение данного вопроса на основе динамической вольт- амперной характеристики, являющейся весьма сложной функцией как скорости нарастания тока, так и температурного состояния контакта (а кстати сказать, эти зависимости почти не исследованы экспериментально), не окажется доступным даже при условии грубо упрощающих допущений. Таким образом, совершенно ясным в этом вопросе является лишь то, что на сегодняшний день аналитического выражения для кривой ступени малого тока при коммутации еще не существует, а поэтому предугадать ее графическое начертание не представляется возможным.
Что же касается графического начертания этой кривой, данной О. Г. Вегнером (рис. 6-1,б), в которой примерно две трети времени коммутации изменение тока происходит по прямолинейному закону, а затем в оставшуюся часть периода ток секции, будучи крайне небольшим и претерпевая небольшие колебания, обеспечивает завершение коммутации практически без тока разрыва, то по этому вопросу можно высказать лишь чисто практические замечания, сущность которых можно свести к следующим положениям:
- В кривой ступени малого тока начальная стадия коммутационного процесса графически изображается прямой линией, несмотря на то, что вольт-амперная характеристика в области значительных плотностей тока мыслится с допущением ∆u = const. Как известно, при подобной аппроксимации контактного сопротивления эта линия будет представляться экспонентой, что и было впервые показано О. Г. Вегнером в его более ранних работах.
- Многолетний опыт в части осциллографирования кривых тока коммутируемого контура на моделях с применением всех известных нам марок щеток как при наличии э. д. с., так и без нее показал, что если щеточный контакт в механическом отношении работает вполне удовлетворительно, то кривые тока коммутируемых секций, принимая самые различные очертания в зависимости от условий коммутации, всегда будут плавными без каких бы то ни было резких изменений тангенсов углов касательных в смежных точках. А между тем в предлагаемой кривой ступени малого тока имеется резкий поворот в кривой, который, с нашей точки зрения, мог быть лишь при условии, если в точке излома кривой резко изменить соответствующим образом э. д. с. ек, что практически выполнить невозможно.
- Что касается экспериментальной проверки кривой ступени малого тока, то здесь очень легко можно впасть в ошибку. Во-первых, кривую, напоминающую ступень малого тока, можно получить, создав условия прямолинейной коммутации с недостаточно хорошо прошлифованным сбегающим краем щетки, а во-вторых, достаточно близкую по очертанию кривую можно получить, создав условия несколько ускоренной коммутации. Вполне понятно, что ни тот, ни другой случаи не имеют ничего обще го с тем, что вкладывается в понятие ступени малого тока.
- Если при посредстве э. д. с. ек осуществляется полный реверс тока ранее размыкания секции щеткой, то как показали многочисленные опыты, в этом случае всегда имеет место ток разрыва обратного направления и возникает искрение от чрезмерной перекомпенсации.
Зависимость амплитудного значения э. д. с. самоиндукции от различных коммутационных параметров
Автор на искусственных аппаратах как с двухпластинчатым коллектором, так и с вращающейся траверсой поставил в свое время много опытов с целью выяснить, как меняется амплитудное значение э. д. с. самоиндукции коммутируемой секции от различных параметров, влияющих на коммутацию [Л. 2-5]. При проведении этих опытов были использованы амплитудный электронный вольтметр и катодный осциллограф. Коммутируемые секции, использованные в опытах, имели параметры, приближающиеся к параметрам машин малой и средней мощности. Для таких параметров коммутируемого контура кривая тока секции имеет характерный изгиб, который при отсутствии ек располагается в средней части кривой, а кривая э. д. с. самоиндукции имеет резко выраженную седлообразную форму, что вполне согласуется с опытными данными К. И. Шейфера, который проводил свои опыты на машинах относительно небольшой мощности.
На рис. 4-12,а приведены кривые еsмакс в зависимости от тока нагрузки для различных марок щеток, по которым видно, что, начиная с тока нагрузки, который автором назван критическим, 1К величина еsмакс при дальнейшем увеличении тока практически сохраняет свое значение. Правда, в отдельных случаях э. д. с. е5Макс может несколько возрастать при увеличении тока или же снижаться, но эти изменения невелики. Было также установлено, что величина еsмакс в небольшой степени зависит от сорта щетки. В свое время по этому поводу автором было высказано следующее предположение: «...При увеличении тока еsмакс практически остается неизменной, но в кривой при этом замечается некоторое уширение пика, что свидетельствует об увеличении ионизированного пространства в контакте щетки, благодаря чему di/dt не изменяется» [Л. 2-5]. Было высказано также предположение о том, что величина еsмакс находится в прямой связи с минимальным значением напряжения электрической дуги для разных марок щеток.
Как показали дальнейшие исследования, электрические дуги, возникающие при завершении коммутации, в отличие от дуг, образующихся при простом размыкании контактов, горят при практически постоянном напряжении, что вполне согласуется с опытами, описанными выше.
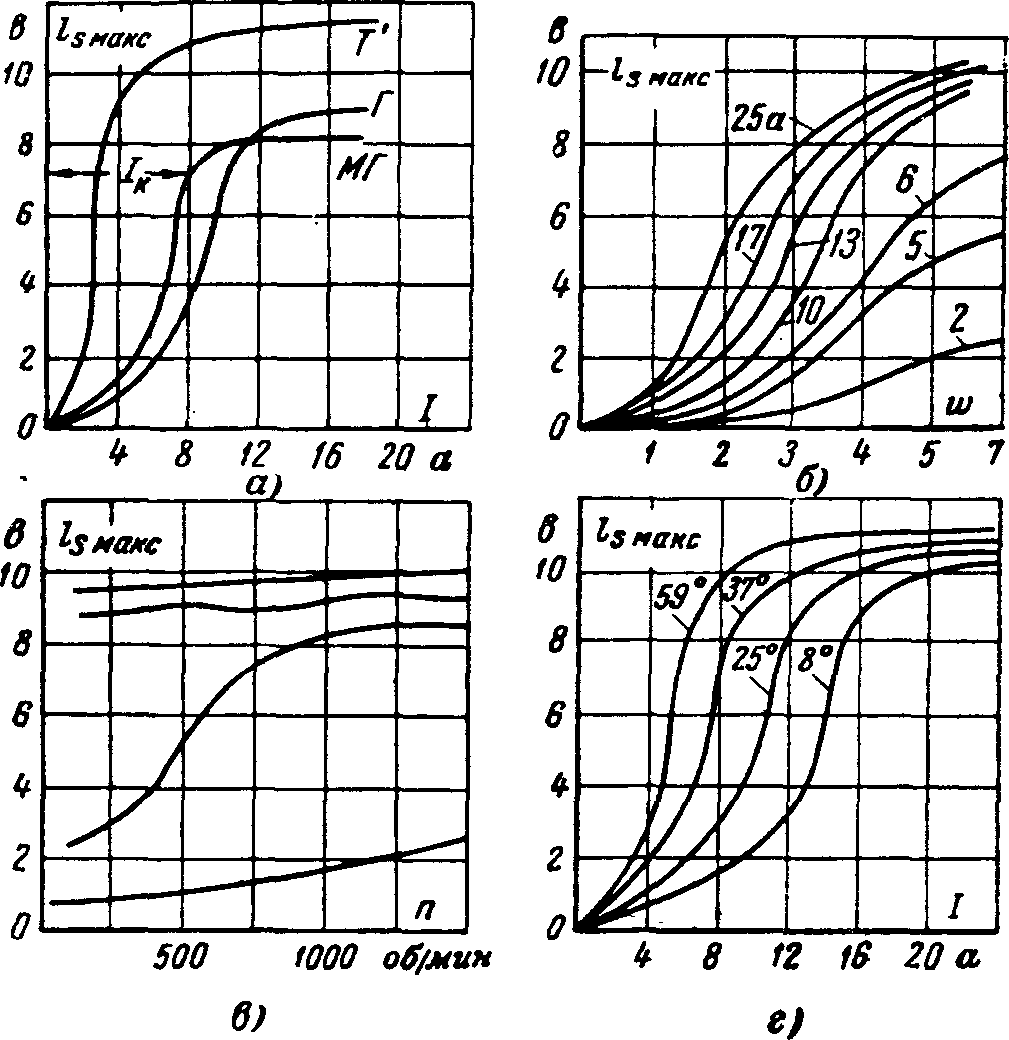
Рис. 4-12. Кривые es макс в зависимости от различных параметров, определяющих коммутацию.
Было также подмечено, что если щетке соответствует несколько меньшее значение еsмакс, как, например, всем щеткам, содержащим металлы, то им соответствуют и меньшие минимальные значения напряжений для возникновения электрической дуги.
Зависимости es макс=f(I), снятые при различных условиях коммутации, со всей несомненностью подчеркивают, что процессы, возникающие в щеточном контакте, чрезвычайно многогранны. Так, например, при относительно малых токах нагрузки, небольшой индуктивности коммутируемых секций и невысокой температуре контакта процессы образования проводимости в щеточном контакте одни, и укладываются они достаточно хорошо в рамки
допущений, принимаемых в основу классической теории коммутации. Если параметры, обусловливающие коммутацию, возрастают, то характер проводимости тока между щеткой и коллектором становится уже иным, и поэтому анализировать получаемые опытные кривые с позиций классической теории уже невозможно. Точно такая картина получается при снятии обычных вольт-амперных характеристик щеточного контакта, очертания которых также доказывают наличие при некоторых условиях качественного изменения механизма прохождения тока через контактный слой. Именно поэтому вопрос о границах применимости классической теории коммутации оказался в настоящее время в высшей степени спорным. Все дело здесь заключается в том, что опытные исследования одних авторов проводились в условиях, когда проводимость тока через контактный слой обеспечивалась главным образом за счет точек непосредственного контакта между щеткой и коллектором, а у других исследователей преимущественно токопрохождение обусловлено было процессами образования ионной, термоэлектронной, а возможно, и автоэлектронной проводимостей, и, наконец, имеются, несомненно, и такие условия опытов, когда эти виды проводимостей тока сочетаются.
На рис. 4-12,б приведены кривые es макс в зависимости от числа витков коммутируемой секции, на которых видно, что если при коммутации ток достиг критического значения, то величина es макс практически сохраняется при дальнейшем увеличении числа витков в коммутируемой секции. На этих же кривых видно, что для каждого тока нагрузки существует критическая индуктивность коммутируемого контура, обусловливающая начальную стадию искрообразования, а поэтому в некоторых установках, предназначенных для определения коммутирующей способности электрощеток, за критерий качества электрощеток принимают эту критическую индуктивность, соответствующую номинальному току, проходящему через щетку [Л. 4-4].
На рис. 4-12,в даны кривые es макс в зависимости от скорости вращения коллектора при прочих неизменных параметрах, определяющих коммутацию. Эти кривые подчеркивают, что если искрения нет, то es макс при увеличении скорости вращения коллектора возрастает примерно пропорционально скорости вращения, а если коммутация заканчивается хотя бы небольшим дуговым разрядам, то дальнейшее увеличение скорости вращения не оказывает заметного влияния на величину es макс. Это положение нашло полное подтверждение при исследованиях коммутационной электрической дуги, проведенных как на искусственных аппаратах, так и на реальных электрических машинах в сравнительно недавнее время. Данные опыты подтвердили, что с увеличением скорости вращения при неизменном токе нагрузки время горения дуги и величина падения напряжения на ней не претерпевают заметных изменений, а если же возрастает ток нагрузки, то практически увеличивается лишь время горения дуги, что вполне согласуется с результатами опытов по снятию зависимости es макс=f(n) (рис. 4-12,в). На основе кривых es макс=f(n) можно усмотреть влияние и механических факторов на дугообразование. Опытами было установлено, что при неизменном токе нагрузки, но при увеличении скорости вращения может наступить дугообразование, которое в данном случае объясняется лишь увеличением степени вибраций щеток, но имеют место и такие случаи, когда увеличение скорости вращения снижает степень искрения, что опять-таки связано с вибрациями, в некоторых случаях уменьшающимися при увеличении скорости вращения коллектора. Степень влияния температуры коллектора на зависимость es макс=f(I) характеризуют кривые на рис. 4-12,г, где видно, что температура коллектора в очень большой степени влияет на величину критического тока, причем большей температуре здесь соответствует меньшее значение критического тока. К сожалению, эти кривые были получены для относительно небольших температур коллектора, а поэтому на основе их нельзя судить о том, как будет вести себя контакт при более высоких температурах. Что касается практики, то в этом вопросе имеется твердо установившееся мнение, что в большинстве случаев в первое время искрение щеток по мере увеличения температуры заметно возрастает, в то время как при нагревах более значительных оно нередко заметно снижается. Кривые es макс=f(I), снятые при различных температурах коллектора, также хорошо согласуются и с вольт- амперными характеристиками щеточного контакта, снимаемыми при различных тепловых состояниях контакта. К сожалению, влияние температуры щеток и коллектора на коммутацию весьма слабо изучено. До последнего времени этому фактору, оказывающему очень большое влияние на коммутацию, не уделяется должного внимания.
Нередко можно встретить журнальные статьи, где излагаются результаты исследований коммутации, в которых отсутствуют какие бы то ни было указания относительно температурного режима щеточного контакта при проведении опытов.
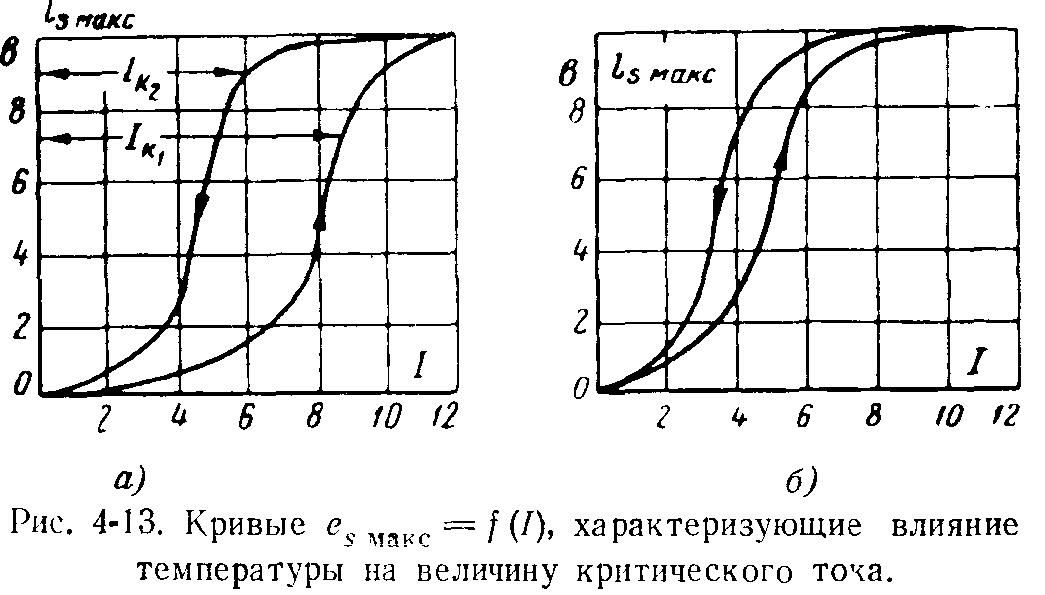
Изменению форм проводимости тока в щеточном контакте свойственна известная инерция, которая свидетельствует о том, что для формирования вновь возникающего вида проводимости тока в щеточном контакте требуется известное время, о чем свидетельствуют кривые на рис. 4-13. Кривая а здесь снята во время опыта, который начинался при температуре коллектора 20° С, причем ток нагрузки повышался со значительными интервалами, во время которых отмечалась вместе с током величина es макс (нижняя кривая). Затем опыт в том же порядке повторяли в обратном направлении (верхняя кривая). Эти две кривые образовали петлю гистерезисного типа, в которой восходящая ветвь имеет значительно больший критический ток, чем нисходящая. Если же этот опыт повторить с нагретым коллектором, то при этом площадь петли заметно уменьшится (рис. 4-13,б). Интересно отметить, что это явление имеет место как при снятии статических вольт-амперных характеристик щеточного контакта с разной выдержкой времени, так и при снятии характеристик динамических.
Автор снимал зависимости es макс= f(I) и при изменении других факторов, оказывающих влияние на коммутацию. Так, например, при отрицательных температурах окружающего воздуха форма кривых es макс=f(I) остается в таком же виде, как и при нормальной температуре, но при этом наблюдается некоторое снижение амплитудных значений у э. д. с. самоиндукции секции es макс. При проведении ряда повторных опытов при низкой температуре замечена значительно большая, чем при нормальной температуре окружающего воздуха, степень стабильности кривых es макс=f(I). Было исследовано также влияние степени влажности воздуха на очертание кривых es макс=f(I). Эти исследования показали, что повышенная влажность окружающего воздуха оказывает благоприятное влияние на коммутацию только при применении твердых щеток, что, видимо, главным образом объясняется уменьшением степени их вибраций. Опыты были проведены и с целью выяснения влияния масляной пленки на коллекторе. Эти опыты показали, что масляная пленка действует так же, как и повышенная влажность, т. е. увеличивает ток I для твердых щеток и уменьшает его для мягких. Слабая заискренность коллектора не влечет заметного ухудшения коммутации также при применении твердых щеток, что, видимо, связано с их абразивными свойствами.
Подводя итог описанию результатов опытов, полученных на основе кривых es макс=f(I), можно с уверенностью сказать, что выводы эти являются весьма четкими и достоверными. Это объясняется отчасти и тем, что установка для их снятия (рис. 4-7) и методика проведения этих опытов чрезвычайно просты, а поэтому все кривые, которые приведены выше, были проверены много раз. Время, которое требуется для повторного опыта, исчисляется несколькими минутами, а поэтому большинство кривых было построено по данным не менее десяти опытов. К тому же следует указать, что эти кривые значительно более стабильны, чем вольт-амперные характеристики щеточного контакта, а поэтому и выводы на основе их дают значительно большую уверенность. Нужно полагать, что повторение таких опытов на более расширенной основе с применением более современных приборов (эти кривые снимались в 1946 г.) даст возможность исследовать очень многие сложные явления коммутации, которые еще далеко не достаточно изучены для решения важных практических вопросов, связанных с искрением электрощеток.
Кривые ∆u макс= f(I) при различных условиях коммутации
В своих первых опубликованных работах автор подчеркнул, что импульсам э. д. с. самоиндукции коммутируемой секции соответствуют и импульсы падения напряжения в щеточном контакте. Для подтверждения этого положения была снята зависимость величин импульсов падения напряжения в сбегающей и набегающей частях щетки от тока нагрузки на реальной машине, причем, как и следовало ожидать, полученные кривые ∆u макс=110 оказались по форме совершенно одинаковыми с рассмотренными выше кривыми es макс=f(I). В статье, опубликованной в 1948 г. [Л. 2-5], автор по этому поводу писал: «Следует отметить, что как пики в кривой es, так и повышенные падения напряжения между щеткой и коллектором появляются одновременно и соответствуют одному и тому же месту в щеточном контакте». И далее: «...а следовательно, если снимать подобные кривые для реальных электрических машин, тс можно и для них выяснить условия, при которых возникает ионизация контакта». Исключительно большим преимуществом этого метода является то, что он в одинаковой мере приложим как к искусственным аппаратам, так и к реальным машинам, причем время, потребное для проведения таких исследований, очень небольшое. Дальнейшее развитие этого метода (см. гл. 5) дало возможность анализировать характер и распределение искрения по всему коллектору.
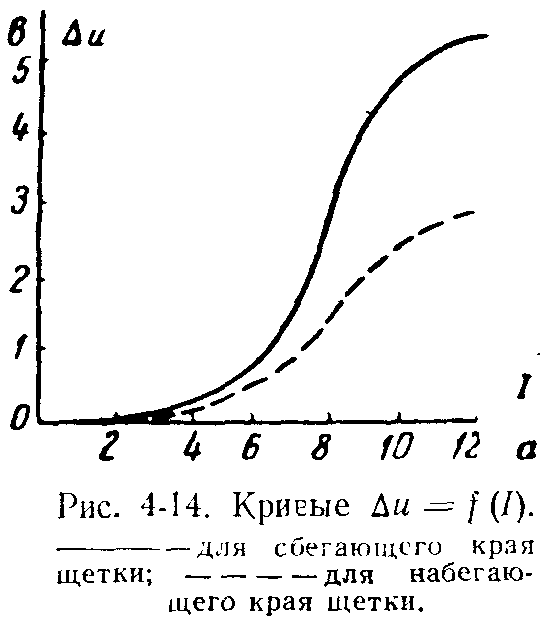
На рис. 4-14 приведены кривые ∆u макс=f(I), снятые для набегающего и сбегающего краев щетки при помощи вспомогательной щетки и амплитудного вольтметра как для катодной, так и для анодной щеток. Как видно из очертания этих кривых, они полностью соответствуют кривым ∆u макс=f(I) и, следовательно, в той же мере характеризуют работу щеточного контакта. В последнее время кривыми ∆u макс=f(I) занимался Л. Л. Лавринович [Л. 4-8]. Он снимал их как посредством обычного амплитудного вольтметра, так и селективного. Эти опыты показали, что оба вольтметра дают приблизительно одинаковые показания. Объясняется это тем, что низкочастотные составляющие, обусловленные зубцовыми и коллекторными пульсациями, выражены здесь незначительно.
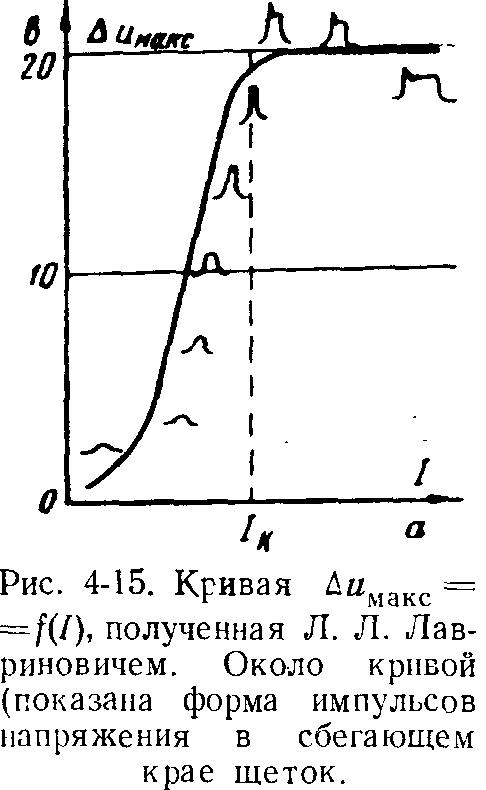
Примененная Л. Л. Лавриновичем аппаратура с достаточно большими разрешающими способностями позволила ему изучать не только характер кривых ∆u макс= f(I), но и наиболее подробно исследовать отдельные стадии разрядных явлений, имеющих место как в набегающей, так и в сбегающей частях щетки. На рис. 4-15 представлена кривая ∆u макс= f(I), полученная Л. Л. Лавриновичем, на которой для отдельных участков показаны кривые напряжения в сбегающей части щеточного контакта. Как видно из очертания этих кривых, импульсы напряжения первоначально, т. е. до образования разрядных явлений в контакте, имеют колоколообразную форму, но при увеличении тока нагрузки их амплитуды постепенно увеличиваются. По мере приближения к критическому току в кривой напряжения все более отчетливо вырисовывается крутой фронт, соответствующий началу образования дугоразрядного процесса. По достижении критического тока в кривой импульса появляется горизонтальный участок, соответствующий напряжению дуги, причем дальнейшему увеличению тока теперь уже не будет соответствовать увеличение амплитудного значения импульса, а лишь уширение верхней части кривой, что подчеркивает увеличение времени горения дуги при ее практически неизменном напряжении. Такое детальное изучение формы импульсов напряжения в щеточном контакте позволило Л. Л. Лавриновичу разработать методику исследования характера искрения щеток реальных электрических машин. Созданная им аппаратура позволила просматривать импульсы напряжения поочередно на всех пластинах коллектора электрической машины, на основе чего делалось заключение о характере искрения и его причинах. Однако этот метод является исключительно сложным и исследования требуют очень много времени, что мешает его широкому внедрению. Л. Л. Лавринович исследовал и характер импульсов в набегающей части щетки, причем выводы этих исследований являются весьма интересными.
Не обнаружив в набегающей части импульсов, соответствующих по форме дугоразрядным процессам, Л. Л. Лавринович заключает следующее: «Медленное снижение переходного падения напряжения наблюдается в тех случаях, когда в начальной фазе коммутации ток протекает через незначительное число проводящих каналов под набегающими краями щеток. Это сопровождается величинами переходных напряжений порядка 2—2,5 в и ведет к возрастанию времени протекания тока через отдельные зерна, что сопровождается увеличением их температуры, воспринимаемой глазом как искрение».
Свои выводы относительно искрения электрощеток Л. Л. Лавринович сформулировал следующим образом: «Наблюдающееся под щетками электрических машин искрение вызывается двумя совершенно различными причинами. Под набегающими краями щеток искрение вызывается большими мгновенными величинами плотности тока в отдельных зернах материала щетки. Под сбегающими краями щеток только очень слабое искрение может вызываться большой плотностью тока в отдельных зернах щетки. Среднее и сильное искрения всегда являются следствием газоразрядных процессов и сопровождаются эрозионным разрушением».
Газоразрядный процесс завершающего этапа коммутации на основе своих экспериментальных исследований Л. Л. Лавринович делит на две характерные части; первую из них он рассматривает как переходный процесс, предшествующий дуговому разряду, и вторую — как собственно дуговой разряд. Эти процессы он характеризует следующим образом: «Напряжение во время переходного процесса достигает 15—25 в; дуговая часть разряда протекает при напряжении 9—14 в. Дуга способна гореть до малых значений тока в конце разряда. Дуговая часть разряда характеризуется незначительным уменьшением напряжения на дуге и спаданием тока в дуге почти по линейному закону».
Классификация искрения электрощеток, сформулированная Л. Л. Лавриновичем, имеет очень большое практическое значение. Есть все основания полагать, что в части искрения набегающего края щеток выводы Л. Л. Лавриновича, идущие в разрез с ранее установившимися представлениями, дадут возможность более правильно подходить к оценке искрения электрощеток и к суждению о качестве коммутации. Однако эти выводы необходимо проверить экспериментально на большом количестве разнотипных машин коллекторного типа с тем, чтобы выяснить, являются ли они общими, т. е. справедливыми для всех разновидностей проявления коммутационного процесса или же могут иметь место случаи, когда и в набегающих краях щеток возникают дугоразрядные процессы.

Во всяком случае, если имеют место хотя бы слабые вибрации щеток, то и в набегающих частях щеток, как показала опытная проверка, существуют газоразрядные процессы.
Опыты И. С. Елохина, проведенные на искусственном аппарате и реальной машине
И. С. Елохин для проверки уравнений тока секции i, дополнительного тока от э. д. с. коммутирующего поля iк и э. д. с. самоиндукции es, полученных им на основе допущения r1= r2=const [уравнения (1-7), (1-8) и (1-10)], поставил опыты на искусственных аппаратах с секциями, параметры которых соответствовали машинам малой и средней мощности. Эти опыты показали, что для машин относительно небольшой мощности полученные опытные кривые достаточно хорошо совпадали с кривыми, которые описываются указанными выше уравнениями. Исключение составляли лишь весьма небольшие участки кривых, которые соответствовали моменту времени, предшествующему окончанию коммутации, а также и ее началу (рис. 4-16). Как уже указывалось выше, коммутационный процесс не может описываться одним уравнением, за исключением случаев, когда проводимость тока в контакте соответствует условию Rщ=const, которые, однако, не могут представлять практического интереса, так как при температурах коллектора и щеток и плотностях тока в щетке современных электрических машин такой вид коммутации исключается.
Кривые тока и э. д. с. коммутируемого контура, снятые И. С. Елохиным при различных температурах щеточного контакта, показывают, что температура влияет не только на очертание данных кривых, но и на степень их стабильности. Если щеточный контакт предварительно не прогрет, то наблюдаемые на экране электронного осциллографа кривые тока и э. д. с. секции имеют различные неровности, которые с течением времени то исчезают, то появляются вновь на различных участках. По мере нагрева коллектора работа щеточного контакта становится все более стабильной, и если в механическом отношении контакт работает удовлетворительно, то при его нагреве эти кривые не имеют никаких неровностей. Есть основание полагать, что замечаемое часто снижение ценообразования при нагреве коллектора объясняется уменьшением вибраций щеток и стабилизацией коммутационных циклов по всему коллектору, происходящим благодаря повышенной температуре контакта между щеткой и коллектором. Однако учитывая исключительную многогранность коммутационного процесса, все имеющиеся в настоящее время формулы для тока и э. д. с. самоиндукции применимы лишь в отдельных частных случаях, да и границы их применимости еще не очерчены определенными рамками.

