- СЕЛЕКТИВНЫЕ СИСТЕМЫ СБОРА И ПРЕОБРАЗОВАНИЯ СОЛНЕЧНОЙ ЭНЕРГИИ.
КОНСТРУКЦИИ И ФОРМИРОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ОБЪЕКТОВ
- 1. Физико-математическая характеристика селективных систем сбора солнечной энергии.
Фокусирующие солнечные коллекторы
И. В. Баум
3.1.1. Теория.
Теоретическое описание является одновременно и необходимым условием рационального использования технического объекта, наиболее емкой формой представления знаний о нем, эффективным инструментом проектирования. Поэтому мы обсудим теоретические вопросы, связанные с принципами работы, функциональными характеристиками и возможными применениями фокусирующих солнечных коллекторов.
Термодинамические аспекты проблемы использования солнечной энергии. Интуитивное представление о возможности использования солнечной энергии ассоциируется с непосредственным тепловым ощущением, вызываемым прямой солнечной радиацией, с восприятием Солнца как источника теплоты. В солнечный день температура отдельных предметов, как известно, может значительно превышать температуру окружающего воздуха. Эти предметы можно рассматривать как аналог лучевоспринимающей поверхности солнечного коллектора. Чтобы рационально использовать эффект перегрева отдельных предметов относительно окружающей среды, необходимо ответить на три вопроса: как это явление возникает, от каких факторов оно зависит, какими конструктивными решениями можно увеличить полезный выход.
Так как речь идет о перепаде относительно температуры окружающей среды, то целесообразно, прежде всего, выяснить, чем определяется эта температура. Для этого рассмотрим баланс энергии в системе Солнце — Земля.
Как излучатель Солнце можно считать абсолютно черным телом сферической формы, радиусом R=6,95·105 км, с поверхностной температурой Тs=5762 К и спектральным максимумом в районе λs=0,50 мкм.
Плотность излучения вблизи солнечной поверхности, согласно закону Стефана-Больцмана, составляет
![]() (3-1)
(3-1)
где σ=5,67·10 8 Вт/(м2· К4) — постоянная Стефана — Больцмана

а при ориентации, исключающей попадание на нее солнечных лучей, охладиться до температуры фонового теплового излучения открытого космического пространства.
Такие резкие колебания поверхностной температуры характерны для небесных тел, лишенных атмосферы. Земная атмосфера обладает относительно невысокой теплоемкостью, поэтому сглаживание локальных суточных колебаний температуры в большей мере связано с тепловой инерцией наземных предметов и поверхностных слоев почвы и воды. Однако непрерывное перемещение больших масс воздуха играет решающую роль в выравнивании глобальных перепадов температур между полярными и экваториальными областями земной поверхности. Следовательно, для использования солнечной энергии необходимо уйти от того термодинамически равновесного состояния, которое реализуется в среднем в земных условиях под влиянием солнечного излучения.
Круг идей, методов и технических решений, направленных на создание специальных неравновесных условий для использования солнечной энергии, чрезвычайно широк и разнообразен. Здесь уже сложились и обособились отдельные направления исследований и технических разработок. Однако в методическом плане полезно наряду с идеей неравновесности указать еще одну общую идею, которую можно было бы условно назвать идеей селективности. Мы остановились на этом не совсем обычном употреблении термина селективности ввиду того, что работа фокусирующего коллектора действительно основана на своеобразном селективном эффекте, суть которого будет пояснена ниже.
Селективные свойства солнечных коллекторов. Из предыдущего изложения можно вывести негативную формулировку принципа работы солнечных коллекторов: для получения температур, отличающихся от средней температуры окружающей среды, необходимо, чтобы условия баланса энергии на лучевоспринимающей поверхности коллектора отличались от средних условий баланса энергии земной поверхности в целом. Позитивная формулировка этого принципа, предполагающая достижение температур выше температуры окружающей среды То, требует ослабления температурной зависимости расходной части баланса так, чтобы равенство между потерями и поступлением энергии достигалось на более высоком температурном уровне Т*>То. В этом случае на некотором промежуточном температурном уровне Тн, удовлетворяющем неравенству То<Тн<Т*, потери будут меньше поступления и условия равновесия будут допускать отвод части энергии для дальнейшего ее использования.
Поясняя идею селективности, остановимся вначале на селективности, связанной с отбором моментов времени, благоприятных для работы коллектора. Естественная периодичность работы коллектора обусловлена суточным вращением Земли вокруг своей оси. Рассмотрим, как и при выводе формулы (3.5), теплоизолированную с тыльной стороны лучевоспринимающую поверхность, находящуюся вне атмосферы на орбите Земли. Предположим на этот раз, что лучи падают на нее не перпендикулярно, а под некоторым углом i Баланс энергии для единицы площади этой поверхности будет иметь вид

Это среднее значение, равное 22°С, близко к среднегодовой температуре экваториальных областей земного шара. Если провести усреднение только по половине периода, когда cost > 0, и считать, что на протяжении другого полупериода как левая, так и правая части уравнения (3.6) обращаются в нуль (нет ни прихода, ни потерь энергии), то средняя температура возрастает до значения
![]() . (3.8)
. (3.8)
что составляет 78° С.
Очевидно, что Земля является малоэффективным приемником. В каждый момент половина земной поверхности вообще не освещается Солнцем. Освещаемая часть поверхности выпуклая и ее площадь в 2 раза превышает площадь ее проекции на плоскость, перпендикулярную лучистому потоку. Так что собственная поверхность Земли в 4 раза превышает эффективную площадь ее приемной поверхности. Именно поэтому плоские теплоизолированные с тыльной стороны приемники, работающие лишь в «дневное» время, когда их поверхность освещается Солнцем, могут нагреваться до температуры, превышающей температурный уровень окружающей среды.
Мы пока не касались вопросов ослабления прямой солнечной радиации в земной атмосфере и конвективного теплообмена, играющего существенную роль в наземных установках. Тем не менее, мы качественно объяснили возможность нагрева тел при плотностях солнечной радиации на уровне земной орбиты, до температур, превышающих среднюю температуру земной поверхности. Основной предпосылкой для такой возможности является направленный характер потока солнечного излучения, достигающего Земли. Именно это обстоятельство позволяет телам с малой тепловой инерцией и поверхностью, обращенной к солнечным лучам, нагреваться днем сильнее, чем окружающий воздух.
Теперь подойдем к проблеме с другой стороны. Зададимся вопросом о предельной температуре, которую можно получить с помощью солнечного излучения. С термодинамической точки зрения при теплопередаче излучением температуру приемника можно довести до уровня температуры источника, т. е. в нашем случае до температуры Τs=5762 К. Однако все вычисленные нами значения ТЕ, Тстах, Тc2π, Тсπ примерно равны 300 К, что в 15—20 раз ниже исходного температурного уровня источника. Это объясняется тем, что рассмотренные нами ситуации помимо теплообмена двух тел — Солнца и приемника — неявно учитывают теплообмен с третьим «телом» — космическим пространством, играющим роль стока теплоты.
Если бы мы поместили плоский теплоизолированный с тыльной стороны приемник непосредственно вблизи солнечной поверхности, то излучение приходило бы на приемник из полупространства, из полусферического телесного угла ΔΩs=2π, а собственное тепловое излучение приемника уходило бы в этот же телесный угол. Здесь теплообмен приемника с другими телами кроме Солнца был бы исключен, и условия баланса в соответствии с уравнением (3.1) были бы обеспечены при температуре приемника, равной температуре солнечной поверхности Tc= Ts.
По мере удаления приемника от Солнца телесный угол видения Солнца ΔΩs<2π постепенно уменьшается, а телесный угол, в который уходит собственное тепловое излучение приемника, остается полусферическим. Угловой радиус солнечного диска ωm и телесный угол ΔΩs связаны с расстоянием от центра Солнца до приемника Rr следующими соотношениями:

В литературе вопросы селективности поглощательной и излучательной способности, за счет которой можно добиться выполнения неравенства (3.11) и повышения температуры приемника, а также вопросы концентрации излучения с помощью зеркальных или линзовых оптических систем, применяемых в целях повышения температуры приемника, рассматриваются обычно отдельно, как независимые. В действительности же эти вопросы на уровне приемной системы в целом оказываются тесно связанными и могут быть рассмотрены с единых позиций. Первые из них относятся к спектральной, а вторые к угловой селективности приемных устройств. Спектральная и угловая селективности системы однозначно определяются направленной спектральной степенью черноты Ε(λ, Ω).
Согласно закону Кирхгофа, направленная спектральная излучательная способность и направленная спектральная поглощательная способность любой системы равны между собой и равны Е (λ, Ω). Благодаря этому уравнение баланса для единицы площади входа любой (в том числе и фокусирующей) системы можно представить в следующем виде:

Случай чисто спектральной селективности подробно рассмотрен в ряде монографий, в частности в [ 1 ]. Поэтому не останавливаясь на подробностях, отметим только саму идею использования спектральной селективности с тем, чтобы провести аналогию с селективностью угловой.
Функции Планка πВо.λ, стоящие под знаками интеграла в формуле (3.16), имеют, согласно закону смещения Вина, достаточно ярко выраженные максимумы при длинах волн Ks=C/Ts, λс=С/Тс (где С=2,9· 103 мкм· К). Наша задача состоит в том, чтобы повысить температуру Тс. Однако ее практически можно считать малой в сравнении с Ts. Поэтому спектральные максимумы функций Βο λ,(λ, Ts) и Βoλ(λ, Тс) достаточно далеки друг от друга, как это показано на рис. 3.1, и энергетически значимые области для этих двух распределений относятся к разным участкам спектра.
Сточки зрения максимального поглощения солнечного излучения предпочтительны высокие значения Ε(λ). В противоположность этому, для снижения уровня потерь Ε(λ) желательно уменьшить. Однако ввиду сосредоточенности спектральных распределений в окрестности своих максимумов для эффективного поглощения солнечного излучения нет необходимости иметь высокие значения Ε(λ) по всему спектру, достаточно, чтобы Ε(λ) были высоки в окрестности λs. Для снижения потерь также не требуется одинаково низких значений Ε(λ) во всем диапазоне длин волн, достаточно, чтобы Ε(λ) были малы в окрестности λc.
Удаленность максимумов λs. К друг от друга позволяет с помощью одной и той же спектрально селективной характеристики Ε(λ) выполнить оба условия.
Аналогичным образом можно использовать угловую селективность приемной системы. Действительно, для того, чтобы эффективно принять (поглотить) поток первичной солнечной радиации, нет необходимости иметь систему с высокой степенью черноты для всех направлений в пределах полусферы. Достаточно, чтобы приемник был черный для излучения, приходящего по направлениям в пределах телесного угла ΔΩs. Если во всех остальных направлениях степень черноты окажется нулевой, то это не уменьшит доли поглощаемого потока, но исключит лучистый теплообмен приемника с каким-либо другим телом кроме Солнца, что позволит довести равновесную температуру коллектора Тс до уровня Ts.
Подобная почти идеальная ситуация реализуется в солнечных печах. Зеркало в форме параболоида вращения, ось которого направлена на центр солнечного диска, фокусирует первичный поток солнечного излучения на малом приемнике, радиус которого составляет 1|216 часть фокусного расстояния параболоида.
С точки зрения приемника зеркало представляет собой вторичный источник, заполняющий все полупространство над лучевоспринимающей поверхностью приемника. От этого вторичного источника на приемник из полусферического телесного угла приходит излучение с яркостной температурой Ts, и ситуация становится аналогичной рассмотренному выше случаю, когда приемник расположен непосредственно вблизи солнечной поверхности.
Параболоидная солнечная печь является своеобразным предельным вариантом фокусирующего солнечного коллектора. Фокусирующий коллектор состоит из двух основных элементов: оптической системы (зеркальной или линзовой) и собственно приемника. В отличие от обычного плоского коллектора, у которого площадь приемной поверхности совпадает с площадью всего коллектора, приемник фокусирующего коллектора по площади во много раз меньше входного отверстия системы.
Оптическая система солнечной печи с точки зрения приемника заменяет реальное Солнце его изображением. При этом яркость изображения не меняется, но занимаемый им телесный угол увеличивается по сравнению с первоначальным ΔΩs во много раз. Так что сама приемная поверхность не должна обладать угловой селективностью.
Если же рассмотреть не один только приемник, а систему в целом, то она будет обладать угловой селективностью. Действительно, на приемник могут попасть только лучи, приходящие из телесного угла ΔΩs. Любой другой луч пройдет мимо приемника и не поглотится системой. Для зеркальной системы справедливо правило обратимости лучей, поэтому собственное излучение приемника после отражения от зеркала также сосредоточится в пределах телесного угла ∆Ωs в направлении солнечного диска.
Таким образом, входное отверстие системы будет эквивалентно поверхности, обладающей угловой селективностью. Направленная интегральная степень черноты будет близка к единице в области ΔΩ5 и будет обращаться в нуль вне пределов этого телесного угла. Граница между нулевым и единичным значением направленной степени черноты для параболоида несколько размыта, но это не меняет сути дела.
Разобранный пример в самом общем виде характеризует основное функциональное свойство фокусирующего коллектора — угловую селективность приемной системы в целом.
- Конструкции. Выше был рассмотрен принцип действия фокусирующего коллектора на примере работы параболоидной солнечной печи. Очевидно, что условием работы такой печи является непрерывное слежение за Солнцем, что представляет определенную трудность. С эксплуатационной точки зрения более предпочтительным является неподвижный коллектор. Ниже будет рассмотрен один из основных типов неподвижных фокусирующих коллекторов.
Принципы конструирования фоклинов. Угловая селективность неподвижного фокусирующего коллектора должна соответствовать не какому-то определенному положению Солнца, а совокупности траекторий видимого движения Солнца по небосводу. Подобными свойствами обладают концентраторы типа фоклинов. Простейшим их вариантом является двугранный фоклин (Д-фоклин), образованный двумя плоскими зеркалами и имеющий форму клиновидного двугранного угла. Другой разновидностью фоклина является изобретенный В. К. Барановым [2] параболоцилиндрический фоклин (ПЦ-фоклин) в котором плоские зеркала заменены фрагментами параболоцилиндра.
К числу селективных по углу оптических систем относятся конические фоконы (К-фоконы) и параболоторические фоконы (ПТ-фоконы); последние также изобретены В. К/ Барановым [3]. Большой вклад в разработку теории и практики применения фоклинов и фоконов сделан американским исследователем Р. Винстоном [4].
В американской литературе зеркальные системы типа фоконов и фоклинов с параболическими образующими объединяются в класс составных параболических концентраторов (CPC-concentrators) и являются частью более широкого класса зеркальных и линзовых концентраторов, не создающих изображения (Nonimaging Concentrators). Этим названием подчеркивается тот факт, что концентраторы излучения могут, не создавая изображения, выполнять свою основную функцию— концентрировать лучистую энергию.
Для гелиотехнических приложений основной интерес представляют двугранные (рис. 3.2,а) и параболоцилиндрические (рис. 3.2,б) фоклины. Каждый фоклин представляет собой цилиндрическую поверхность. На рис. 3.2. показаны также поперечные сечения, основные параметры Д-фоклина и ПЦ-фоклина и угловые зависимости коэффициентов пропускания τ=τ (ξ).
Соотношения, определяющие геометрию Д-фоклинов, имеют следующий вид:
D - d = 2Н tg а; D = d/sin а (3.17)
Для Дфоклииов и ПЦ-фоклинов введены единые обозначения: D — ширина входного отверстия, d — ширина выходного отверстия, Н — высота фоклина.
Из рис. 3.2,а легко определить ширину зеркальной полосы Д-фоклина
l = H/cosa (3-18)
Д-фоклин, габариты которого удовлетворяют соотношениям (3.17), обладают следующим свойством. Поток лучей, параллельных его плоскости симметрии, войдя в систему через входное отверстие, после ряда отражений выходит из фоклина через выходное отверстие. При этом средний геометрический коэффициент концентрации будет равен:

Таким образом, интегральная полусферическая излучательная способность двугранного фоклина, отнесенная к площади его входного отверстия, равна его параметрическому углу ξс=α, выраженному в радианной мере. Эта величина при больших углах а не превышает единицы, так как вычисление справедливо для углов а=π/4.
Пропускательная способность Д-фоклина в зависимости от угла ξ изображена на рис. 3.2,а. Как видно, Д-фоклин, обладая преимуществом с точки зрения простоты конструкции, имеет и недостатки. Его работа при углах ξ≠θ сопровождается заметными потерями первичного потока излучения, тем большими, чем больше угол ξ.
Для устранения этого недостатка приходится применять более сложную зеркальную конструкцию — ПЦ-фоклин. Его угловая характеристика коэффициента пропускания изображена на рис. 3.2,6

Для построения образующих ПЦ-фоклина можно использовать следующий прием (рис. 3.3). По заданным значениям H и К вычисляют габариты входного и выходного отверстий (3.26) и фокусное расстояние параболы (3.27). На расстоянии друг от друга проводятся две параллельные прямые «in» и «out», соответствующие сечениям плоскости входного и выходного отверстий. На прямой «out» отмечается точка «О», через нее перпендикулярно прямым «in», «out» проводится ось симметрии сечения фоклина У. Точки А', А на прямой «out», отстоящие от оси у на расстояние d/2, указывают габариты выходного отверстия. Точки В', В на прямой «in», отстоящие от оси у на расстояние D/2, указывают габариты входного отверстия. Далее, строится вспомогательная декартова система координат с осями Х'У'. Для этого через точку А проводится прямая, параллельная направлению АВ. Эта прямая и есть ось У', она составляет с осью У угол а. Точка А должна являться точкой фокуса параболической образующей «правого» зеркала фоклина АВ. Поэтому начало «О'» вспомогательной декартовой системы координат отстоит от точки А' на расстояние f. Ось X' проходит через точку «О'» перпендикулярно оси У'. В координатах X', У' строится парабола
![]() (3.28) которая должна соединить точки АВ. Отрезок параболы между точками АВ и является искомой образующей «правого» зеркала.
(3.28) которая должна соединить точки АВ. Отрезок параболы между точками АВ и является искомой образующей «правого» зеркала.
Образующая «левого» зеркала А'В' симметрична отрезку параболы АВ относительно У. Для контроля формы поверхности зеркал при сборке панели коллектора надо помнить, что касательная к отражающей поверхности в точке В перпендикулярна плоскости коллектора, а касательная в точке А составляет с плоскостью коллектора угол (π/4+α/2).
Интересно сравнить два рассмотренных выше типа фоклинов. При одинаковых параметрических углах а фоклины одинаково концентрируют излучение, падающее перпендикулярно плоскости коллектора. Обе системы имеют примерно одинаковую излучательную способность входного отверстия, равную соответственно а и sincа. Полоса пропускания излучения (по углу ξ) у Д-фоклина в 2 раза шире, чем у ПЦ-фоклина. Однако в пределах |ξ|<α Д-фоклин пропускает в среднем лишь 3/4 потока излучения. Кроме того, для Д-фоклина характерны многократные отражения лучей, а для ПЦ-фоклина однократные, поэтому реальное пропускание Д-фоклинов может резко уменьшиться при использовании зеркал с коэффициентом отражения р < 0,9.
При одинаковых концентрациях К и высотах Н Д-фоклины имеют несколько более широкие входные (и соответственно выходные) отверстия, чем ПЦ-фоклины
![]() (3.29)
(3.29)
Так что, при равных входных отверстиях Dд=Dпц, Д-фоклины имеют несколько меньшую высоту
![]() (3.30)
(3.30)
Сами по себе эти различия не могут свидетельствовать в пользу Д-фоклинов, так как геометрия фоклинов допускает преобразования подобия. Гораздо большие трудности при изготовлении ПЦ-фоклинов может вызвать неплоская форма их отражающей поверхности. Однако различия габаритов следует иметь в виду при оценке суммарной площади зеркальной поверхности, приходящейся на единицу площади в плоскости коллектора. При К=5 ПЦ-фоклины требуют в полтора, а при К=3 вдвое большей площади зеркал, чем Д-фоклины. Это обстоятельство стимулировало разработку специальных «усеченных» конструкций ПЦ-фоклинов, в которых исключена «верхняя» часть поверхности, не играющая существенной роли в повышении концентрации.

Рис. 3.1. Спектральные распределения солнечной радиации на орбите Земли (Ts=5762 К, Xs=0,5 mkm) и излучения черного тела при «земных» температурах солнечного коллектора (Тс=415 К, К=7 мкм)

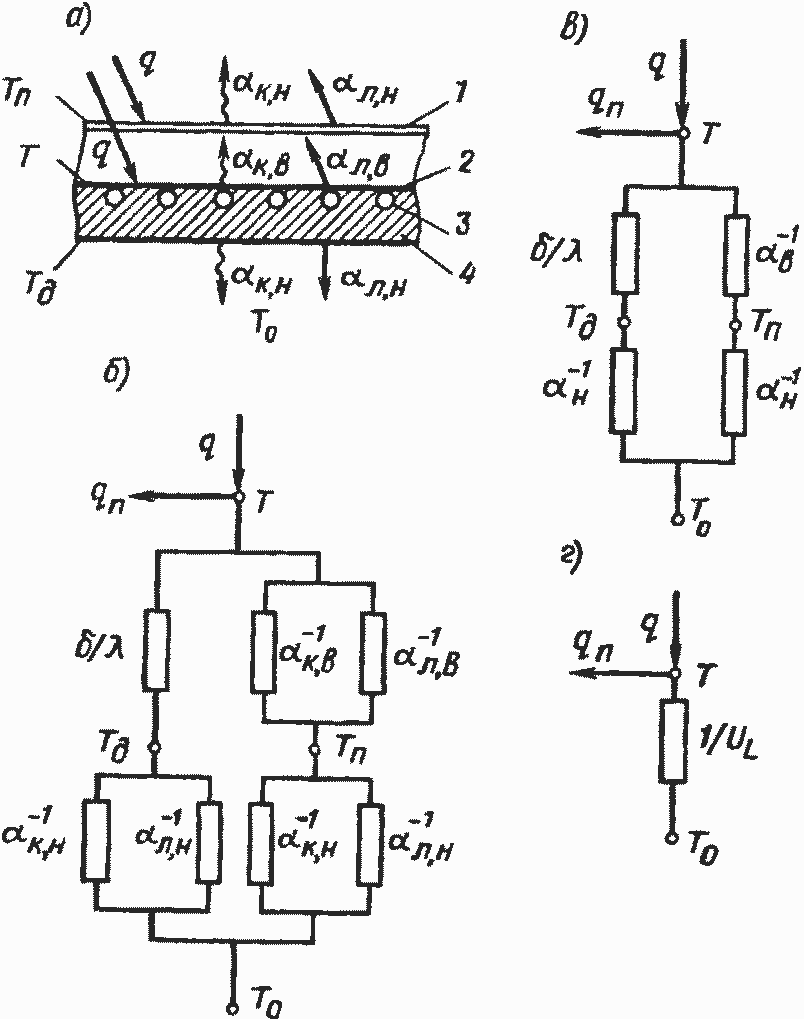
Рис. 3.2. Коллекторы с двугранными (а) и параболоцилиндрическими (б) фоклинами: 1 — прозрачное покрытие; 2 — отражающая поверхность; 3 — каналы с теплоносителем; 4 — тепловая изоляция
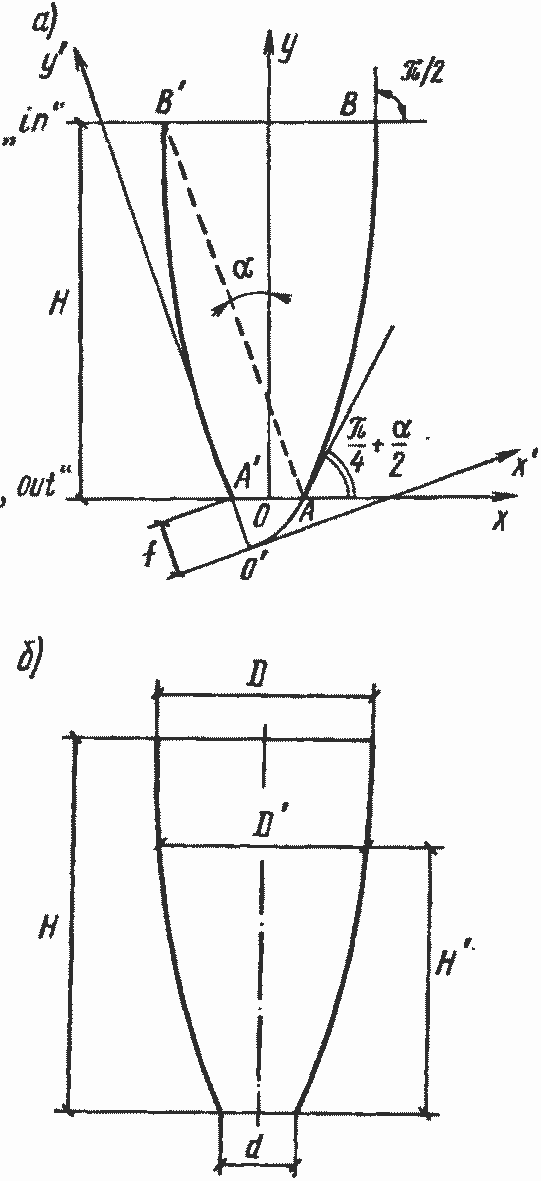
Рис. 3.3. Построение образующих ПЦ-фоклина (а) и соотношение габаритов усеченного ПЦ-фоклина (б)
Рис. 3.4. Схема тепловых сопротивлений плоского коллектора
Выбор рационального коэффициента усечения требует специальных расчетов. Но приблизительно можно обойтись и чисто графическим решением задачи, построив предварительно образующие ПЦ-фоклинов по заданному исходному коэффициенту концентрации К и выбрав базовым размером, например, D. Затем по чертежу определяют высоту Н' (отсчитанную от выходного отверстия), на которой ширина полости фоклина составляет заданную долю от первоначального габарита входного отверстия D (см. рис. 3.3). Эту ширину принимают за новый габарит входного отверстия Dпц, отбросив часть зеркальной поверхности выше уровня Н'. Новый коэффициент концентрации будет иметь значение K'=D'/d.
Таблица 3.1 Габаритные размеры усеченных ПЦ-фоклинов


Характеристики различных типов коллекторов. Основным параметром, определяющим эксплуатационные характеристики коллектора, является коэффициент потерь Ul. Фокусирующие системы, как мы видели выше, позволяют уменьшить потери, связанные с собственным тепловым излучением лучевоспринимающей поверхности. Для наземных солнечных установок необходимо учитывать конвективные потери, которые также снижаются в коллекторах с фокусирующими элементами.
Суть параметра Ul подробно рассматривается в монографии [5] Это легко пояснить на примере обычного плоского солнечного коллектора, схема тепловых сопротивлений которого изображена на рис. 3.4 Солнечные лучи, проникая через прозрачную изоляцию 1, падают на рабочую поверхность 2 (рис. 3.4,а). Тепловая мощность q, выделяющаяся на единице площади рабочей поверхности, частично отводится теплоносителем, протекающим по каналам 3 (обозначим эту часть через qn), а частично через элементы конструкции коллектора уходит в виде тепловых потерь в окружающую среду. При прочных равных условиях плотность потока потерь в расчете на единицу площади рабочей поверхности оказывается пропорциональной разности температур рабочей поверхности Т и окружающей среды То. Коэффициент пропорциональности этой линейной зависимости и называется коэффициентом потерь Ul.
Поток тепловых потерь, проходя через изоляцию тыльной стороны коллектора 4 и распространяясь в зазоре между 1 и 2, преодолевает различные тепловые сопротивления (рис. 3.4,б), определяемые параметрами изоляции σ, λ и коэффициентом внутренней («в») и наружной («н») конвективной («к») и лучистой («л») теплоотдачи а. Последовательно упрощая схему тепловых сопротивлений (рис 3.4, в), можно вывести соотношение


Эта запись по форме напоминает выражение для плотности потока теплоты, передаваемой с коэффициентом теплопередачи Ul через теплообменную поверхность от среды или источника с температурой Т* к среде с температурой Т. По этой аналогии можно ввести понятие эквивалентного источника, а коллектор рассматривать как своеобразный рекуперативный теплообменный аппарат с площадью теплообменной поверхности, равной S.
Теперь легко перейти к случаю неоднородных распределений температуры по рабочей поверхности, возникающих при постепенном прогреве теплоносителя по мере движения его вдоль поверхности теплообмена. Выражения (3.32) — (3.37) остаются и в этом случае справедливыми, но приобретают смысл локальных соотношений. Причем температура источника не меняется вдоль поверхности теплообмена, что можно интерпретировать как случай бесконечного расхода теплоносителя в первом контуре теплообменника.
Известно, что температурный напор (Τ*—Τ) вдоль поверхности теплообмена в такой ситуации экспоненциально уменьшается в направлении движения теплоносителя во втором контуре, т.е. в нашем случае в направлении движения реального теплоносителя, протекающего через солнечный коллектор. Так что связь между входной и выходной температурами теплоносителя будет иметь вид


Формулы (3.49) с очевидностью показывают, что хотя при минимальных требуемых температурных перепадах фокусирующие коллекторы могут оказаться менее эффективными, чем плоские из-за потерь в зеркальной системе и уменьшения рабочего времени, обусловленного ограниченным «видением» небосвода, тем не менее фокусирование следует применять при необходимости нагрева теплоносителя до высоких температур, которые для плоских коллекторов могут оказаться вовсе недостижимыми.
Подробный отчет об экспериментальных исследованиях характеристик фокусирующих коллекторов приведен в работе [6]. Характерным примером являются результаты испытаний фокусирующего коллектора с ПЦ-фоклином и концентрацией Х=3. Этот коллектор испытывался как в лабораторных условиях, так и в натурных. Параметрический угол фоклина составлял а=18°. Коллектор имел защитное прозрачное покрытие с пропускательной способностью τ=0,90 и рабочую поверхность с поглощательной способностью Ас=0,94. Алюминиевое зеркало имело отражательную способность р=84. С учетом многократных отражений расчетная величина среднеэксплуатационной отражательной способности зеркальной системы составляла р=0,80. На первой стадии эксперимента в лабораторных условиях было определено значение эффективного коэффициента потерь, составившее U=3,0 Вт/(м2· °C).
На рис. 3.5 представлены результаты натурных испытаний этой конструкции зимой в районе Чикаго. По оси абсцисс отложено отношение перепада температур ∆T к плотности потока суммарной прямой и рассеянной радиации в плоскости коллектора. Переменные, использованные в работе [6], приведены к нашим обозначениям. По оси ординат отложен к.п.д. коллектора. Прямая 3 соответствует условиям среднего ясного зимнего дня. Отклонения экспериментальных точек, отмеченных крестиками, от этой прямой определяются в основном различием в соотношении между прямой и рассеянной радиацией в конкретные дни эксперимента. В особо ясные дни, отмеченные квадратами, при повышенной прозрачности атмосферы и малой относительной величине рассеянной радиации к.п.д. коллектора по отношению к суммарной радиации заметно повышался. Для дней с плохой прозрачностью атмосферы, отмеченных на рисунке треугольниками, наблюдалась противоположная картина. Среднеэксплуатационное значение эффективного коэффициента потерь для зимней серии экспериментов составило U1=2,7 Вт/(м2·°C). Для сравнения на рис. 3.5 приведены характеристики типичных плоских коллекторов с одинарным (прямая 1) и двойным (прямая 2) остеклением, имеющих в 2—2,5 раза более высокие коэффициенты потерь. Данный пример показывает, что соотношение (3.45) не всегда точно выполняется на практике. Это объясняется тем, что конструкции теплоизоляции плоских и фокусирующих коллекторов не совсем идентичны.
Оценим с помощью данных рис. 3.5 два конкретных частных случая. Пусть уровень плотности потока суммарной радиации в плоскости коллектора составляет 600 Вт/м2, что соответствует прямой радиации в 700 Вт/м2, падающей в 9 ч утра по солнечному времени на коллектор под углом 45°, и рассеянной радиации в 100 Вт/м2.
Если требуемый температурный перепад нагрева теплоносителя составляет ΔT=30°, то все три типа коллектора будут работать примерно с одинаковой эффективностью и их к.п.д. будет составлять около 55%. Если же температурный перепад утроится, увеличившись до 90°, то к.п.д. фокусирующего коллектора снизится до 45%, тогда как к.п.д. плоского коллектора с одинарным остеклением резко уменьшится и составит всего 20%. Плоский коллектор с двойным остеклением также будет иметь низкий к.п.д. около 30%.
Приведенные численные оценки позволяют качественно разграничить области применения плоских и фокусирующих коллекторов. Плоские коллекторы могут применяться во всех случаях, когда непосредственно потребляемой является низкопотенциальная тепловая форма преобразования солнечной энергии. К числу таких ситуаций относится нагрев воды в летних открытых бассейнах, горячее водоснабжение летом и т.п. Плоские коллекторы можно также применять в сочетании с тепловыми насосами и в системах отопления, однако их непосредственное применение в подобных системах ограничено, как правило, лишь районами с мягким климатом. Фокусирующие же коллекторы, напротив, можно использовать в отопительных системах на любых географических широтах с единственным условием достаточного числа солнечных дней в холодный период года. Особый интерес фокусирующие коллекторы представляют для систем преобразования солнечной энергии, например, для автономных энергетических установок термодинамического типа, использующих в качестве рабочего тела низкокипящие жидкости.
Следует отметить, что при всей перспективности фокусирующих коллекторов их массовое производство пока не освоено, тогда как суммарное годовое производство плоских коллекторов в отдельных странах уже исчисляется сотнями тысяч квадратных метров. Альтернативным путем улучшения теплотехнических характеристик коллекторов можно назвать вакуумные методы изоляции и применение селективных поглощающих и отражающих покрытий.
Анализируя современные конструкторские разработки по солнечным коллекторам, можно отметить тенденцию к комплексному применению различных средств снижения тепловых потерь, в частности, применение фокусирующих коллекторов с вакуумной тепловой изоляцией. Наряду с этим ведутся разработки по совершенствованию самой оптической схемы фокусирующих коллекторов: применению приемников различной геометрии и асимметричных конструкций зеркальной поверхности, упрощению формы образующих отражателя с целью удешевления его изготовления. При этом большое внимание уделяется изучению угловой селективности как зеркальных, так и линзовых систем и анализу их оптико-геометрической пропускательной способности.
Параллельно с совершенствованием фокусирующих коллекторов на основе различных модификаций фоклинов разрабатываются упрощенные конструкции, представляющие собой разновидность двустороннего плоского коллектора, помещенного между двумя плоскими однократно отражающими зеркальными крыльями.
3.1.3. Оптимизация.
Наряду с чисто оптическими оптимизационными задачами, связанными с конструктивной реализацией основных принципов и идей создания фокусирующих конструкций, коллекторов, практическое использование солнечных коллекторов с фокусирующими элементами выдвигает внешние оптимизационные задачи. Оптимизация наиболее высокого уровня связана, как правило, с экономическими характеристиками проектируемых систем. Для постановки столь общих задач имеющаяся информация зачастую оказывается недостаточной ввиду неустановившегося характера стоимостных показателей новой техники. Однако существуют задачи более низкого уровня, представляющие самостоятельный чисто технический интерес и связанные с системным согласованием конструктивных параметров оптических элементов и режимов их работы.
Режимы работы солнечных коллекторов. Задачи режимной оптимизации возникают уже в плоском коллекторе, когда требуется определить оптимальный угол его наклона к горизонту. Для фокусирующего коллектора с концентратором типа фоклин эта задача предполагает системное согласование параметрического угла коллектора, угла наклона его плоскости к горизонту в любой период года и частоты изменения его ориентации. Целевые функции подобных частных оптимизационных задач зависят от назначения солнечных систем, номинальных температурных режимов их работы и существенно меняются в зависимости от того, предназначена ли система для удовлетворения потребностей в тепловой энергии или служит элементом преобразователя солнечной энергии, например является первым контуром солнечной термодинамической энергоустановки.
Наметим лишь некоторые подходы к моделированию режимов работы фокусирующих коллекторов. Первым элементом моделирования является выбор модели прихода солнечной радиации. Геометрическая часть этой задачи сводится к описанию движения Солнца по небосклону. Она решается сравнительно просто и подробно описана в различных руководствах по использованию солнечной энергии, в частности в монографии [5]. Если координатные оси X, У, Z местной локально-географической системы координат направить соответственно на юг, восток и в зенит, то единичный вектор l, задающий направление на центр солнечного диска, будет иметь следующие компоненты:
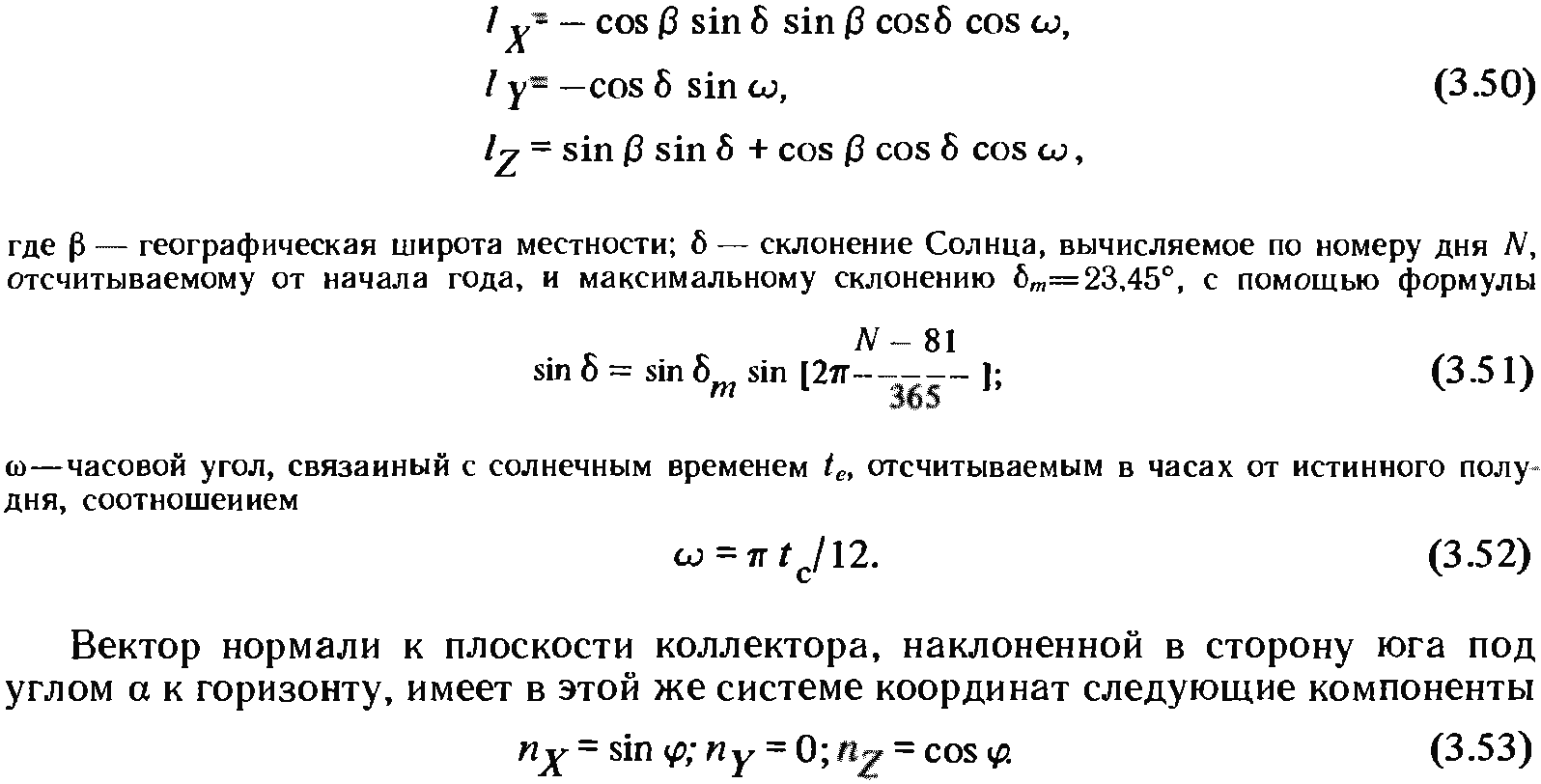

Таблица 3.2 Параметрический угол, необходимый для обеспечения заданной длительности рабочего дня ПЦ-фоклина на 22 июня

По этой таблице разумные пределы выбора параметрического угла составляют а=6—15°. Рабочий день фоклина даже при малых параметрических углах достаточно продолжителен. Это особенно важно, если вспомнить материалы предыдущего раздела, где была продемонстрирована ограниченность рабочего дня плоского коллектора, связанная с низкой эффективностью его работы при повышенных температурных режимах.
Уменьшение параметрического угла фоклина требует более частой коррекции его ориентации. Фоклин с параметрическим углом а= 18°, рассмотренный в предыдущем разделе, требует всего двукратной коррекции в год с двумя положениями — «зимним» и «летним». Фоклины с параметрическими углами порядка 10° требуют ежемесячной коррекции, с углами в 6° — еженедельной. Однако этот вопрос должен более детально обсуждаться при проектировании конкретных типов коллекторов с учетом характера их тепловой нагрузки.
Оптимизация среднеэксплуатационных характеристик. При моделировании среднеэксплуатационных характеристик коллектора необходимо учитывать статистику прихода солнечной радиации в конкретном районе расположения солнечной установки. Простейшей методикой может быть приближение, предложенное В. Г. Кастровым, обнаружившим сильную корреляционную зависимость между уровнем прямой солнечной радиации и высотой Солнца над горизонтом в ясные дни.
Соотношение между прямой qo, рассеянной qр и суммарной солнечной радиацией определяется по В. Г. Кастрову метеорологической солнечной постоянной qм=1,25±0,04 кВт/м2 и коэффициентом поглощения χ
![]()
(3.56)
Величины χ для каждого месяца должны быть предварительно вычислены по средним многолетним данным метеонаблюдений.
В математическую модель следует ввести также среднестатистическую обеспеченность отсутствия облачности. Эту величину, как и коэффициент поглощения χ, следует относить к месячному интервалу вне зависимости от того, как часто меняется в процессе корректировки ориентация коллектора.
Системы утилизации солнечной энергии как с плоскими, так и с фокусирующими коллекторами имеют особенность, связанную с нерегулярным характером поступления солнечной радиации. Эта особенность определяется своеобразным эффектом насыщения, который наблюдается при расчете коэффициента замещения, указывающего долю нагрузки, покрываемой с помощью солнечной установки. Основная причина данного эффекта, как правило, связана с несовпадением графиков нагрузки и прихода солнечной радиации; она может быть устранена полностью лишь в случае применения систем долгосрочного аккумулирования.
Эффект насыщения приводит к тому необычному для традиционных топливных систем положению, когда максимальная эффективность применения солнечного оборудования соответствует минимальным значениям коэффициента замещения. Стремление создать высоконадежную чисто солнечную систему может привести к неоправданному увеличению ее размеров и прежде всего размеров солнечного коллектора, который значительную часть времени будет работать в недогруженном режиме. Оптимальные размеры солнечных систем соответствуют, как правило, невысоким значениям коэффициента замещения на уровне 0,4—0,7.
Не вдаваясь в подробности этой самостоятельной большой темы, отметим, что переход к коллекторам с улучшенными тепловыми характеристиками, как правило, снимает некоторые неопределенности в постановке задач экономической оптимизации, так как зависимости коэффициента замещения от размеров системы при заданной нагрузке имеют для таких коллекторов явно выраженный излом, указывающий в первом приближении положение рабочей точки на графиках коэффициента замещения.

