В разностных методах моделирования процесс речного стока Q(t), представленный в среднемесячных или среднедекадных величинах, разлагается на две составляющие: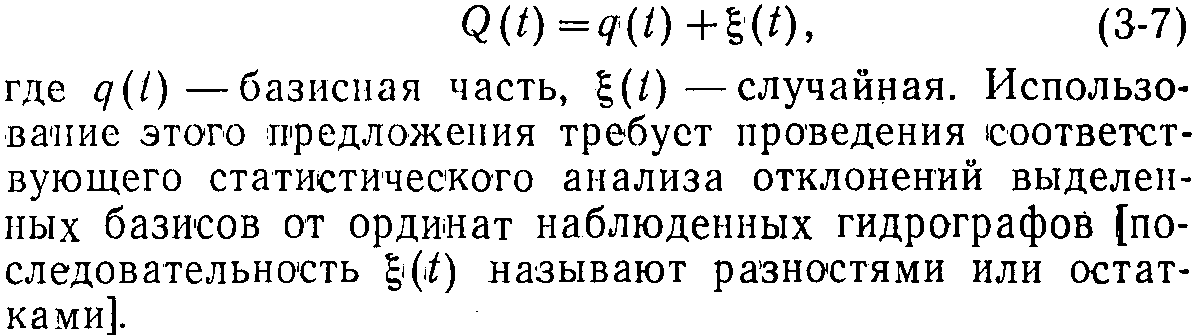
Для многомерных процессов речного стока в нескольких створах наиболее простым было бы такое его представление, в котором случайные части процесса были бы некоррелированными нормально распределенными последовательностями с нулевым математическим ожиданием и единичной дисперсией. В этом случае моделирование речного стока и расчеты его регулирования можно было бы проводить наиболее точно, т. е. без необоснованных допущений, и исключительно просто.
Способов выделения базисов, т. е. закономерной части речного стока, можно предложить достаточно много. Наиболее простыми могут быть детерминированные базисы: гармоническая составляющая с одной гармоникой, сумма нескольких гармоник и, наконец, в простейшем виде базис может быть некоторой детерминированной функцией времени.
Более сложными являются одношаговые регрессионные базисы, использованные в упоминавшихся выше работах [Л. 31, 52, 83].
Достаточно надежных исследований характеристик остатков (случайной составляющей процесса) после применения детерминированных и регрессионных одношаговых базисов не проводилось. Выполненные в «Энергосетьпроекте» расчеты показали, что для всех рассмотренных в работе рек при использовании простейших детерминированных базисов полученные остатки не являются выборкой из одной совокупности, их распределение не соответствует нормальному, и эти последовательности скоррелированы во времени. Эти проработки показывают, что использование детерминированных базисов, как правило, нецелесообразно (Л. 2).
Более благоприятные результаты получены при использовании одношаговых регрессионных базисов. В этом случае в качестве базиса q(t) использовались величины, зависящие только от предыдущего состояния процесса [Л. 52]:
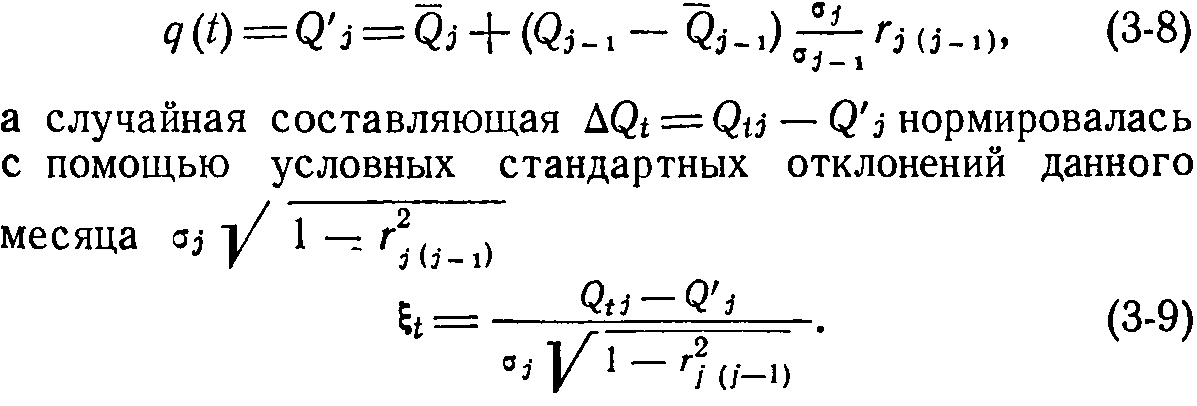
Выделенная таким способом случайная составляющая процесса стока для ряда рек имела нулевое математическое ожидание, единичную дисперсию и следующие значения коэффициента асимметрии:
р. Нарын............................................. 0,48
р. Кура ................................................ 1,12
р. Енисей.......................................................................... 0,41
Для выделенных последовательностей был произведен спектральный анализ, который свидетельствует о том, что данные последовательности не коррелированы во времени.
Сделанная проверка однородности последовательностей свидетельствует о том, что с вероятностью 99,9% эти последовательности являются выборками из одной генеральной совокупности. Проведенный анализ показал, что данные последовательности не противоречат нормальному закону распределения вероятностей.
Исследование коррелятивной связи между случайными составляющими процесса стока разных рек, в том числе и рек одного бассейна (в нашей работе исследовались и отдельные притоки р. Ангары), показало практическую независимость случайных составляющих. Это дает возможность использовать данный метод разделения процесса для моделирования стока нескольких рек, случайного водопотребления и испарения одновременно. При этом моделирование каждого ряда можно осуществлять независимо. Однако этот вывод является предварительным: он нуждается в опытной проверке и для бассейнов других рек.
Моделирование рядов при рассматриваемом способе разделения процесса на составляющие описано в [Л.21, 52] и вытекает непосредственно из выражения (3-9):
![]() (3-10)
(3-10)
Таким образом, можно считать, что данный метод выделения базисной составляющей процесса речного стока дает возможность считать оставшуюся случайную часть процесса независимой во времени с распределением, близким к нормальному с нулевым математическим ожиданием и единичной дисперсией. Однако для принятия окончательного решения о пригодности данного метода моделирования для практического использования следует рассмотреть ряд вопросов.
- Первый из них был поднят еще в [Л. 52]. Он заключается в том, что при моделировании искусственных гидрологических рядов (в данной схеме выделения базиса) в некоторые месяцы имело место появление отрицательных величин стока. Очевидно, для крупных рек появление отрицательных величин стока противоречит физическому смыслу явления. Поэтому в [Л. 52] была предложена операция превращения при моделировании отрицательных величин стока в нуль, которая при не очень большом числе отрицательных величин — 2—3,% (например, 100—200 из 6 000 смоделированных) несущественно изменяла параметры распределения искусственного ряда. В наших проверочных расчетах для указанных выше трех рек отрицательные величины месячного стока были получены только на двух: р. Куре и р. Енисее. Число таких величин было на порядок меньше, чем в (Л. 52). Так, на р. Куре на 12 000 смоделированных месячных величин отрицательными были только 13, т. е. 0,1%, а на р. Енисее — 35, т. е. 0,3%.
- Для любых искусственных рядов необходима проверка соответствия параметров распределения рядов, полученных в результате моделирования, исходным параметрам распределения. Применительно к месячным расходам воды проверку можно производить двумя способами: а) непосредственно по всем месячным расходам как единому ряду и б) по сечениям ряда за одноименные месяцы. В последнем случае, кроме нормы Сυ, Cs требуется сопоставление коэффициентов корреляции между смежными месяцами.
По первому способу результаты проверки соответствия параметров 1000-летних рядов заданным наблюденным параметрам представлены в табл. 3-2.
Таблица 3-2
Сопоставление параметров единого ряда среднемесячных расходов
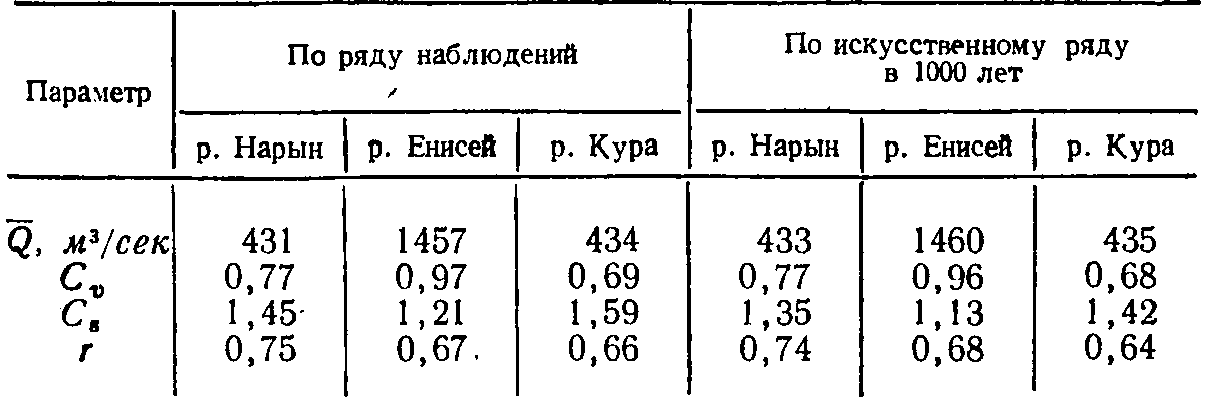
Все параметры вычислены без учета отрицательных величин стока, которые были заменены нулями.
Из табл. 3-2 видно, что при рассмотрении месячных расходов как единого ряда совпадение параметров искусственных рядов с исходными практически получено полное. Сравнение с исходными параметров распределения рядов по сечениям за одноименные месяцы приведено только для двух рек в табл. 3-3. В ней под (j-i) подразумевается коэффициент корреляции расходов реки за данный месяц с расходами реки за предыдущий месяц. В графе Cs0 приведены оценки коэффициента асимметрии сечения за одноименные месяцы, вычисленные по ряду наблюдений методом моментов.
Таблица 3-3
Сопоставление параметров стока за отдельные месяцы
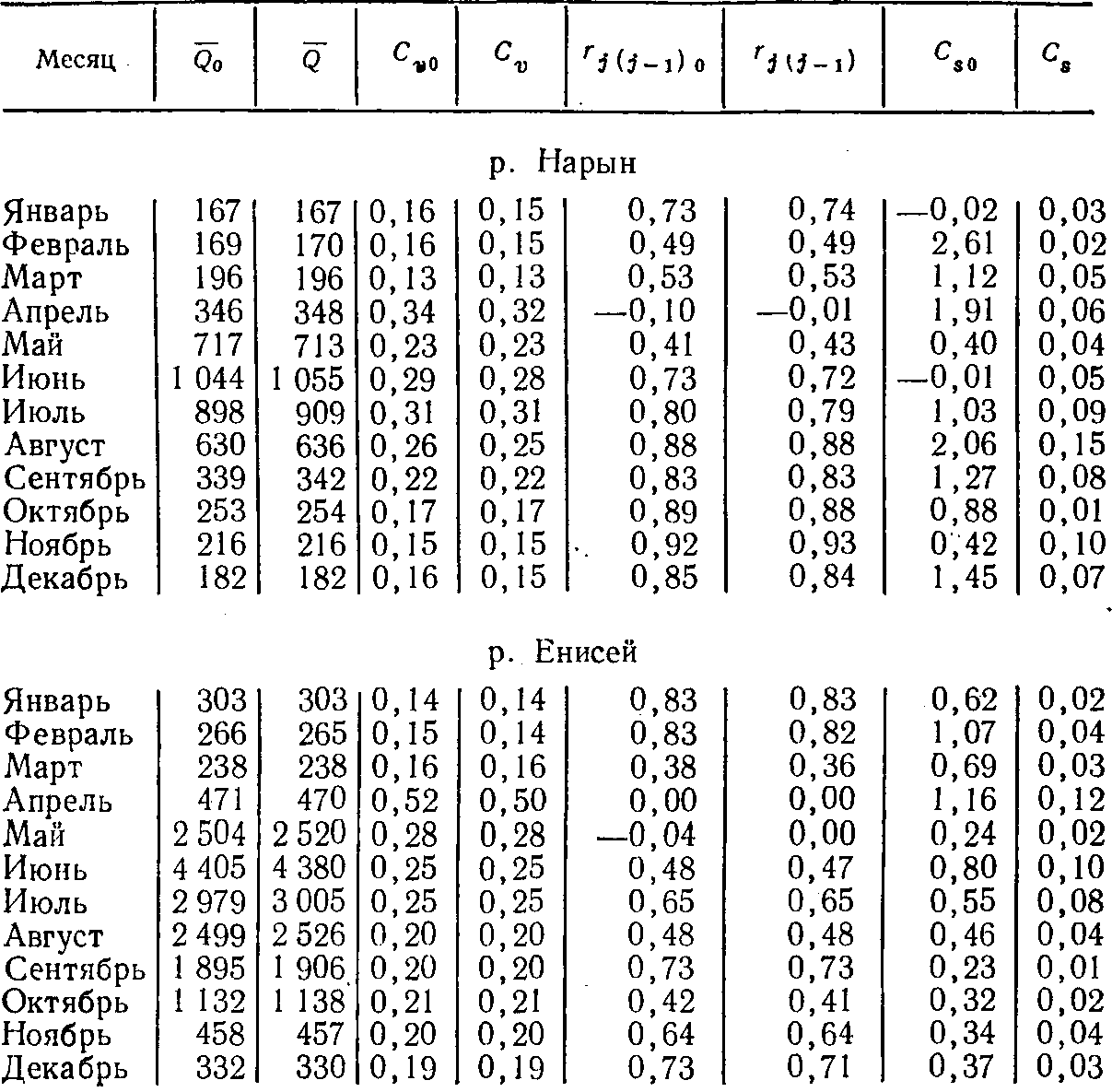
Приведенные данные свидетельствуют, с одной стороны, о том, что в рассматриваемом методе моделирования получаются последовательности, достаточно хорошо соответствующие нормальному закону распределения вероятностей. С другой стороны, данные табл. 3-3 показывают, что в отдельные месяцы асимметричность остатков может быть существенной, т. е. в рассматриваемом методе выделения разностей случайная составляющая лишь с приближением может считаться нормально распределенной.
Окончательное общее решение вопроса о виде теоретической функции распределения вероятностей для остатков месячных величин стока в настоящее время, по нашему мнению, еще не может быть получено ввиду недостаточных исследований в этой области. Возможно, что для рек различных районов, имеющих разные условия стокообразования, решения могут оказаться Неодинаковыми. Поэтому при разработке метода моделирования месячных величин стока целесообразно предусмотреть возможность использования распределений с любой асимметричностью.
При использовании простой марковской цепи в работе [Л. 83] для учета при моделировании асимметричности распределений остатков рекомендуется введение следующей поправки:
(3-11)
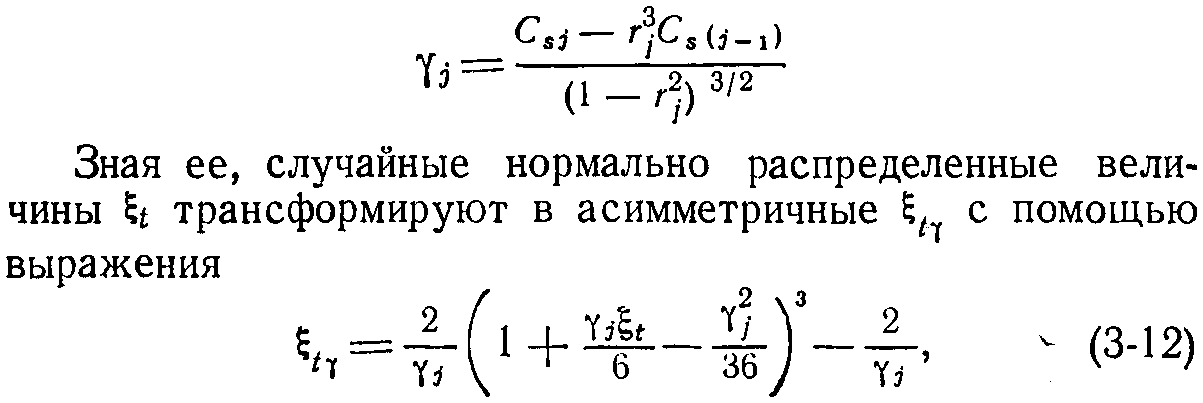
где j — индекс месяца (изменяется от 1 до 12), — непрерывный ряд нормально распределенных величин. Использование приведенной поправки дает возможность получать асимметрично распределенные последовательности, что подтверждается работой [Л. 83].
Приведенные выше две проверки качества искусственных рядов достаточны при проведении расчетов сезонного и годового регулирования речного стока.
- Для проведения по искусственным рядам расчета многолетнего регулирования стока указанных выше двух проверок недостаточно. Здесь требуется рассмотрение соответствия характеристик годового стока рек, так как они существенно влияют на величину необходимой емкости водохранилищ.
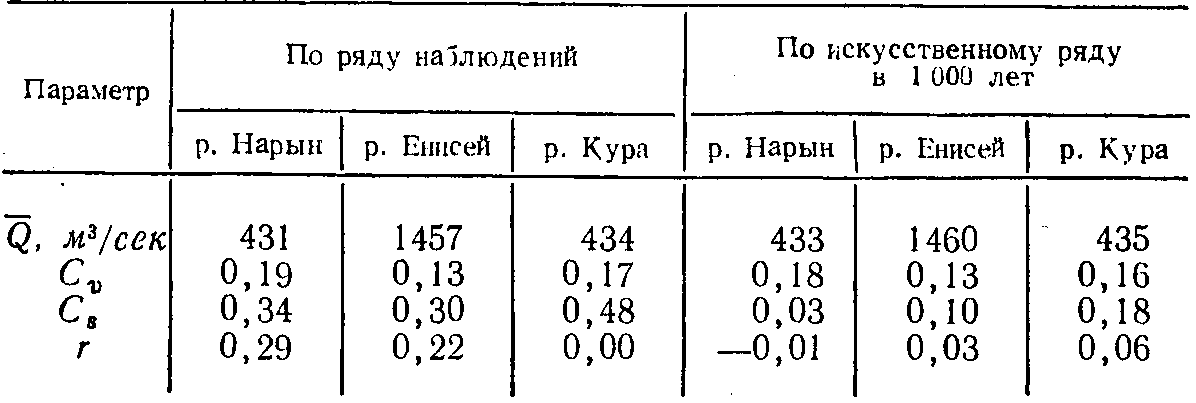
Характеристики годового стока для рассмотренных рек и их сопоставление с соответствующими характеристиками, полученными по искусственным рядам, представлены в табл. 3-4.
Приведенные данные показывают, что норма стока и коэффициент вариации годового стока искусственного ряда совпадают с исходными, а коэффициенты асимметрии и корреляции между смежными членами не совпадают. При этом имело место преуменьшение и коэффициента асимметрии и коэффициента автокорреляции, причем последний в искусственных рядах практически был равен нулю. Преуменьшение коэффициента асимметрии, как следует из работы [Л. 21], приводит к завышению необходимой емкости водохранилищ, а (преуменьшение коэффициента корреляции — к занижению ее величины, т. е. действие этих несоответствий параметров взаимно компенсирующее.
Таблица 3-4
Сопоставление параметров ряда среднегодовых расходов
Тем не менее для осторожности, видимо, целесообразно следовать рекомендации [Л. 21] и использовать данный метод разложения процесса стока и его моделирования для расчетов сезонного регулирования, а для расчетов многолетнего регулирования — лишь в случае отсутствия коррелятивной связи между смежными членами ряда годового стока.
Для более общего случая рассмотрим еще один возможный вариант разложения процесса стока на составляющие.
В качестве базиса q(t) принимаем величины, зависящие от предшествующих состояний процесса:
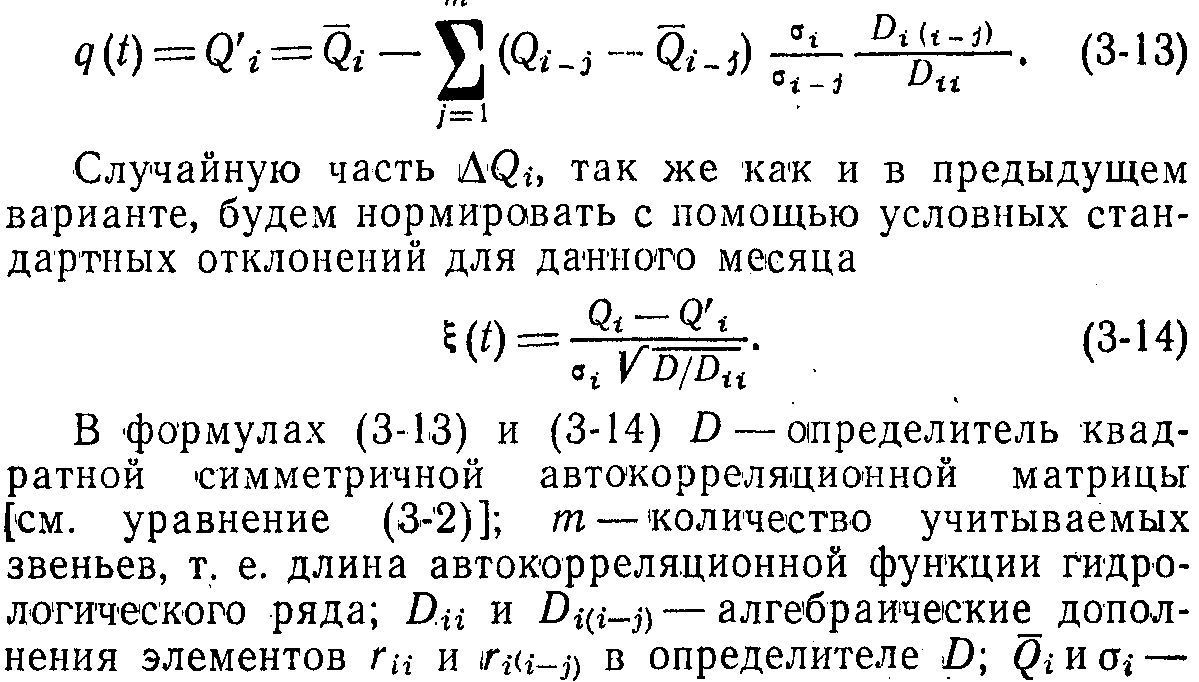

Здесь все обозначения аналогичны приведенным выше. Одним из основных в рассматриваемой схеме выделения базисной части процесса является вопрос о количестве учитываемых предшествующих состояний процесса т. Его выбор может осуществляться, например, с помощью методов, описанных в [Л. 60], исходя из критерия минимума дисперсии прогноза. Вполне очевидным является стремление выбирать число т по возможности небольшим, т. е. начинать расчет для т—2 и лишь при недостаточно хорошем совпадении параметров переходить к большим т.
Этот вопрос для других целей и иными методами исследовался Н. А. Картвелишвили [Л. 37]. Он указывает, что «... увеличение т сверх четырех, а иногда сверх трех приводит не к улучшению, а к ухудшению совпадения. Это объясняется тем, что функции распределения вероятностей, по которым производится розыгрыш, не удовлетворяют точно так называемому обобщенному уравнению Маркова, т. е., строго говоря, являются функциями перехода марковского процесса лишь с некоторым приближением».
Использование рассматриваемого метода разложения процесса покажем на примере р. Нарына. Полученные в результате разложения остатки (случайная составляющая) являлись с вероятностью 99,9% некоррелированной выборкой из одной генеральной совокупности. Они имели распределение, близкое к нормальному, с нулевым математическим ожиданием, единичной дисперсией и коэффициентом асимметрии, близким единице. Указанные результаты получены для нескольких значений величины т, т. е. при разном количестве учитываемых в разложении предшествующих состояний процесса.
Рассмотрим результаты сопоставления параметров искусственных рядов и параметров исходных. Этот анализ проведем на примере трех значений величины т: 2, 3 и 12. Как и в предыдущем варианте, параметры единого ряда среднемесячных расходов совпадают с исходными. Для сечений одноименных месяцев полученные результаты близки результатам предыдущего варианта выделения составляющих и поэтому для сокращения места здесь не приводятся. Для ряда среднегодовых величин стока параметры даны в табл. 3-5.
Таблица 3-5
Сопоставление параметров ряда среднегодовых расходов р. Нарына
(без учета поправки на асимметричность)

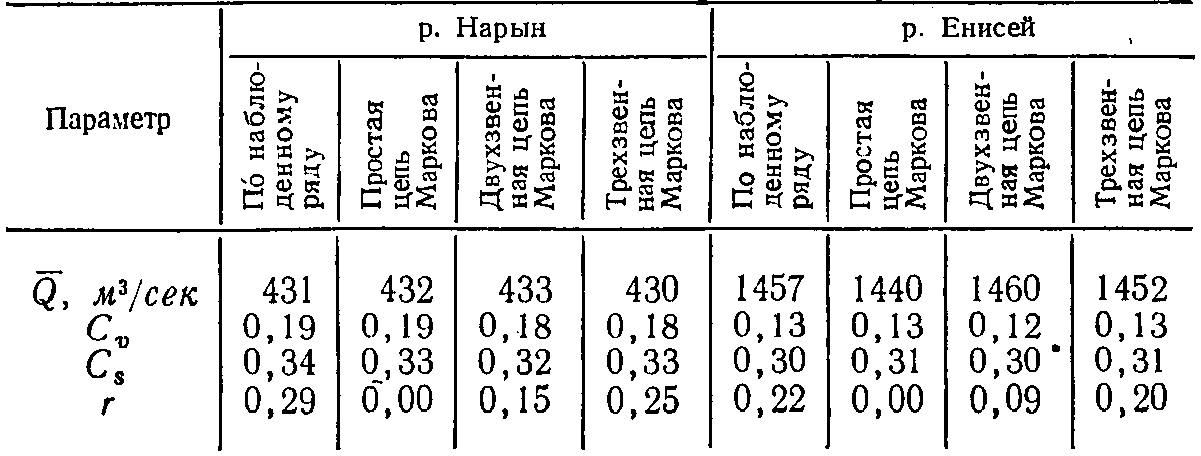
Приведенные данные, полученные при моделировании рядов без учета поправки (3-16) на асимметричность, свидетельствуют: 1) о нецелесообразности использования в разложении большого числа звеньев в марковской цепи (см. выше); 2) о возможности с помощью выбора соответствующего количества учитываемых при моделировании предшествующих состояний процесса получить достаточно хорошее совпадение с заданными следующих параметров искусственных рядов годового стока: Q, Cv, r. Несколько хуже совпадают характеристики асимметрии. При использовании поправки (3-16), а для схемы простой цепи — поправки (3-11) результаты моделирования 1000-летних рядов для рек Нарына и Енисея представлены в табл. 3-6. Приведенные данные свидетельствуют о полном совпадении всех параметров годового стока при описании месячного стока рек трехзвенной марковской цепью. Совпадение с исходными параметров месячного стока также полное (для сокращения места эти характеристики здесь не приводятся).
Таблица 3-6
Сопоставление параметров годового стока (с учетом поправки на асимметричность)
Для р. Нарына не было отмечено отрицательных величин в искусственном ряду месячного стока при его моделировании, для р. Енисея в рассматриваемом случае число отрицательных величин несколько сократилось по сравнению с моделированием по схеме простой марковской цепи (30 вместо 35). Для полной ликвидации возможности появления отрицательных величин стока во всех случаях, видимо, самым простым способом может быть использование при моделировании логарифмических или каких-либо иных его трансформаций (см. выше и [Л. 38]).
О методах моделирования речного стока для каскадов гидроузлов и о возможности применения к ним описанного приема было кратко отмечено выше. Резюмируя сказанное, можно отметить, что описанный прием позволяет при моделировании месячных величин стока рек получать достаточно хорошее соответствие заданном параметров и месячного, и годового стока. Вероятность появления отрицательных величин стока в отдельные месяцы исключительно мала, и операции замены отрицательных величин на нулевые, на их модули или на равные некоторой постоянной положительной величине (например, Q) для практических расчетов вполне допустимы.
Исследование закономерностей и моделирование случайно изменяющегося водопотребления и испарения в этом случае полностью аналогично изложенному выше в § 3-2, и дополнительных пояснений не требует.

