В своем стремлении познать мир мы так или иначе используем свои представления о симметрии и асимметрии геометрических форм окружающих нас предметов и их расположении в пространстве.
Когда-то симметрию называли “гармонией мира”. Поиски гармонии мира привели И. Кеплера к открытию законов движения планет. Затем идеи симметрии пространства и времени, развитые применительно к макромиру, проникли в кристаллографию и химию при описании структур кристаллов и химических соединений. Но особенно значительные успехи достигнуты при создании квантовой картины микромира и, в частности, строения частиц, образующих атом. Оказалось, что законы сохранения энергии, импульса и углового момента являются, по сути дела, следствиями общих принципов симметрии [27—35].
В последнее время столь эффективный метод исследований снова возвратился в свою “alma mater” — в макромир, где его плодотворно используют при анализе так называемых “диссипативных” структур. Структуры возникают в открытых системах, удаленных от состояния термодинамического равновесия. Эти образования, как считают авторы работ [36—39], поддерживаются в упорядоченном виде благодаря непрерывной диссипации энергии.
Взяв за основу достигнутый уровень знаний, попытаемся в этом разделе раскрыть принцип формирования течений в оболочках звезд и ядер галактик.
Изученные нами ранее структуры потоков в атмосфере и океане, несомненно, относятся к диссипативным. Для удобства расчета мы полагали, что возникающие в водной и воздушной средах циркуляционные контуры являются закрытыми системами, обменивающимися с окружающей средой лишь теплом. На самом же деле реальные системы нельзя считать подлинно закрытыми. Корреляция между скоростями частиц в потоках как раз и нарушается из-за их взаимодействия с неподвижными слоями воды и воздуха. Очевидно, что мы имеем дело с открытыми системами, поддерживаемыми в виде симметричных образований внешним потоком солнечной энергии. Именно эти гидродинамические структуры в состоянии переправить энергию с экватора Земли к полюсам в гораздо большем масштабе, чем может быть обеспечен обычной теплопроводностью.
Строго говоря, определение этих структур как “диссипативных” отражает лишь одно свойство систем — способность непрерывно рассеивать кинетическую энергию, преобразуя ее в тепловую. Однако мы видим, что природные гидродинамические образования действуют как системы, способные самопроизвольно воссоздавать теряемую кинетическую энергию. Поэтому правильнее было бы называть эти структуры “креационно-диссипативные” (лат. creatio — создание, творение; dissipatio — рассеяние). Но предлагаемое название имеет слишком общий характер. Нам же хотелось бы оттенить в нем индивидуальные свойства классифицируемых объектов. Поэтому целесообразно сохранить в названии введенный нами ранее вид силового поля, взаимодействующего с тепловым потоком. Итак, в дальнейшем мы будем придерживаться следующей терминологии: “гравитационно-.., ротационно-.., компрессионно-диссипативные” структуры. При таком подходе из названия можно сразу же получить представление о направлении движения циркулируемых потоков и возможной интенсивности предполагаемых процессов.
Отметим некоторое отличие в методах расчета процессов получения кинетической энергии и ее дальнейшего расходования индивидуальными циркуляционными ячейками. Если в первом случае нас, в основном, интересовала интенсивность силового поля, в котором проявляется тот или иной термодинамический эффект, а размеры и форма каналов и контактирующих в них фаз не имели существенного значения, то во втором случае ситуация меняется на противоположную. Здесь уже именно геометрические характеристики гидродинамических структур и соотношение фаз определяют величину энергетических потерь. Происходит это потому, что законы трения неинвариантны относительно изменения пространственного масштаба систем или, иначе говоря, преобразования подобия. Влияние пространственных факторов на диссипацию энергии еще более возрастает при коллективном действии циркуляционных ячеек, к изучению которых мы сейчас приступаем.
1.2.1. Гравитационно-диссипативные структуры
В качестве аналога гравитационно-диссипативных структур, возникающих в горном озере (рис. 1, часть I), примем так называемые ячейки Бенара [40].
Приводимый на рис. 6 снимок, увеличенный примерно в 25 раз, демонстрирует гексагональную конвективную структуру в слое силиконового масла глубиной 1 мм при равномерном нагреве снизу и воздействии окружающего воздуха сверху. Если верхняя поверхность свободна, то течение создается главным образом неоднородностями поверхностного натяжения, а не плавучестью. Свет, отраженный от алюминиевых хлопьев, демонстрирует подъем жидкости в центре каждой ячейки и ее опускание на краях. Время экспозиции составляет 10 с, тогда как время движения жидкости поперек ячейки от центра к краю равно 2 с. Фото V/G. Velarde, M. Yuste, J. Salan.
Ячейки Бенара, попадая в область течений, принимают удлиненную форму [17].
Внешний вид ячеек свидетельствует о том, что при осуществлении того или иного процесса природа стремится соблюдать свой основной принцип — принцип экономного использования пространства и энергии. Экономия достигается за счет расположения потоков в определенном порядке. Как известно, гексагональная структура обладает двумя видами симметрии — трансляционной (переносной) и поворотной шестого порядка.

Рис. 6. Конвекция, создаваемая поверхностным натяжением (конвекция Бенара)
Представим себе, что в нашем горном озере резко повысилось количество тепла, поступающего из земных недр. Наблюдая за поведением потоков, мы очень скоро убеждаемся, что одновременно с ростом тепловой нагрузки увеличивается число циркуляционных ячеек. В конце концов, вся водная акватория будет втянута в циркуляцию. Вновь возникающие циркуляционные контуры сравнительно равномерно разместятся в объеме озера, создав гидродинамическую конструкцию, похожую в идеальном варианте на ту, что дана на рис. 6.
При дальнейшем повышении температурного напора согласованное движение отдельных частей потоков нарушается. Возле дна озера образуется слой пара, снижающий интенсивность теплообмена. Система перейдет в пульсационный режим с хаотичным выбросом значительных объемов пара в различных частях озера. Произошедшее нарушение “упорядоченности” означает, что система теряет те виды симметрии, что допускались сложившимися условиями ее взаимодействия с окружающей средой.
Теперь обсудим энергетическую сторону затронутой проблемы.
Как известно, равновесное состояние любой изолированной системы является ее наиболее вероятным состоянием. Устойчивость в этом случае характеризуется тем, что при малом отклонении от него изменение энтропии отрицательно, ибо в условиях равновесия энтропия достигает своего максимального значения. Причем равновесные структуры существуют благодаря консервативным силам, действующим внутри самой системы.
Напомним, что общая тенденция для неравновесных систем — превращение всех видов энергии в тепловую. Это превращение приводит систему к наиболее вероятному состоянию.
Критерий устойчивости сильно неравновесного состояния, сформулированный П. Гленсдорфом и И. Пригожиным, состоит в том, что производная по времени от второй вариации энтропии должна быть положительной. Как видим, неравновесная система становится все более и более устойчивой и упорядоченной при максимальной скорости диссипации кинетической энергии, возникающей, в свою очередь, в результате пространственной передачи внешнего потока тепла.
Здесь мы сталкиваемся с весьма необычной интерпретацией второго начала термодинамики: энтропия рассматривается не как мера безостановочного соскальзывания системы к состоянию хаоса, а как прародительница вновь возникающего порядка.
Возвратимся к изложенному нами в первой части книги гравитационному эффекту. Более или менее надежные результаты расчета процесса естественной циркуляции мы получили лишь для испарителя с конкретными геометрическими размерами. Очевидно, что внутренний КПД hое индивидуального циркуляционного контура учитывает уровень диссипации энергии в подъемном канале, а общее количество полученной кинетической энергии определяет, по сути дела, ее расход на трение в опускном канале. Так что для анализируемой системы были найдены достаточно точные значения энтропии.
Пространственные характеристики локальных циркуляционных контуров в горном озере явно отличаются от геометрических параметров промышленных аппаратов. Поэтому при расчете сопротивлений каналов течению потоков приходится подбирать свои эмпирические формулы. В связи с трудностями полевых измерений найденные значения энтропии локальных систем оказываются крайне приближенными, но все же эти величины позволяют представить себе физическую картину процесса.
Попытаемся преодолеть возникшие трудности, привлекая принятые методы обобщения опытных данных.
Перейдем к математическому описанию пространственно-временных структур, возникающих в горном озере. Предположим, что над озером нам удалось разместить непроницаемый колпак, позволивший собирать и измерять количество образующегося пара. Обозначим объем пара, выделившийся ко времени τ, символом Vτ, а общий объем, полученный к концу процесса, через Vмах. Далее допустим, что на дне озера периодически изменяется температурный перепад. Проследим за изменением скорости парообразования с помощью графика. Для этого отложим на оси ординат отношение Vτ/Vмах, а на оси абсцисс время τ. В итоге мы получим семейство S-образных кривых (рис. 7).
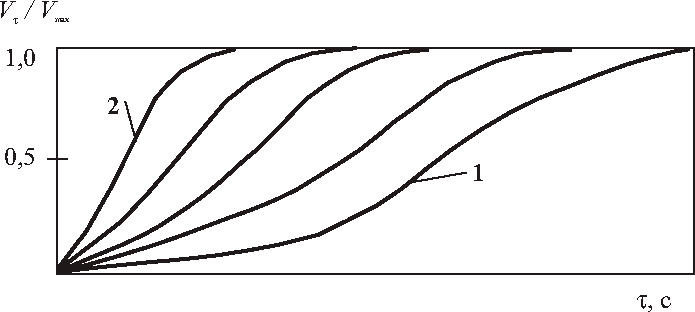
Рис. 7. Кинетика образования пара при изменении температурного напора на дне горного озера
1 — температура воды ≈ 40°С; 2 — температура воды ≈ 85°С.
Каждому температурному напору соответствует определенное число циркуляционных ячеек. При малой разности температур между дном и водой число циркуляционных ячеек невелико. В этом случае вода прогреется лишь в зонах действия циркуляционных контуров. Выход пара над озером при этом незначительный, что соответствует расположению S-образных кривых вблизи оси абсцисс. С увеличением температурного напора весь объем воды в озере прогревается до температуры кипения, число циркуляционных ячеек возрастает до некоторого максимального значения, а S-образные кривые поднимаются к оси ординат.
Все кривые характеризуются точкой перегиба, откуда явствует, что скорость парообразования в начальной стадии процесса возрастает, достигает максимума и с возникновением пульсационного режима в конце процесса падает.
В ряде случаев фазовые превращения рассматривают как химические реакции. Такой подход дает возможность проводить оценку вероятности равновесных процессов по единой методике [41]. При дальнейшем сравнении оказалось, что не только термодинамические соотношения, но и кинетические характеристики процессов можно оценивать по одним и тем же уравнениям.
В нашем случае испарение подчиняется обобщенному уравнению химической кинетики гетерогенных процессов, молекулярно-статистический вывод которого дан Б.В. Ерофеевым [42], а именно
![]() (I.1)
(I.1)
где k — константа скорости процесса парообразования, определяемая сложившимися в озере температурными условиями; n — постоянная, зависящая от свойств пара и жидкости.
Поскольку S-образные кривые представляют, по сути дела, две состыкованные между собой экспоненты, то в точке перелома значения k и nизменяются. Характер изменения этих величин определяют [43, 44] методом двукратного логарифмирования уравнения (I.1).
Уравнение формальной кинетики, приведенное выше, позволяет корректно обобщить экспериментальные данные, но не вскрывает энергетической стороны процесса. Вместе с тем, уравнение (I.1) дает нам возможность трактовать точку перегиба S-образных кривых как достижение креационно-диссипативной структурой своей устойчивости. В этом случае необходимо учитывать члены второго порядка в выражении для отклонения энтропии от ее максимального значения.
Наша система с приближением к точке перегиба становится все более и более устойчивой и упорядоченной. При этом рост диссипации кинетической энергии со временем достигает в ней своего максимального значения. Данное положение легко проверяется, поскольку в нашем распоряжении имеются по аналогии с испарителем характеристики одной из типичных индивидуальных циркуляционных ячеек (хотя и приближенные), а число ячеек можно подсчитать, наблюдая за гладью озера. При этом численно удается подтвердить, что при отклонении рассматриваемой системы от идеальной симметрии, аналогичной симметрии ячеек Бенара, скорость производства в ней энтропии будет снижаться.
Теперь, анализируя таким же образом ротационно-диссипативные структуры, получим дополнительную полезную для нас информацию.
1.2.2. Ротационно-диссипативные структуры
Создание теории образования вихрей и их взаимодействия между собой является одной из ключевых задач гидромеханики. С историей этого вопроса и деталями многочисленных опытов можно ознакомиться по обстоятельным монографиям [45—47].
Вехами прошлого большой значимости были работы Дж. Тейлора [48] и А.Н. Колмогорова [49], а также материалы ряда конференций [46].
Турбулентность можно описать с помощью иерархии вихрей, или ячеек турбулентности, которые одновременно существуют во многих различных масштабах длин. К настоящему времени разработано несколько моделей процесса, которые, впрочем, продолжают уточняться.
Мы уже знаем, что “холодные” потоки, двигающиеся с полюсов планет к экватору (”жгуты”), вращаются вокруг своей оси. Поэтому их можно рассматривать как вихри. Например, “Красное пятно” на Юпитере совершает один оборот вокруг своей оси за 6 суток, в то время как сама планета — примерно за 10 часов. Пятно движется вокруг оси планеты несколько медленнее, чем окружающая его южная тропическая зона. Примерно за 30 лет пятно запаздывает на полный оборот планеты.
Определенное представление о системе вихрей, перемещающихся таким же способом по шаровой поверхности, мы можем получить, изучая данные по спиральным галактикам.
Рассмотрим те галактики, у которых наблюдается регулярный спиральный узор. Классификация этих галактик принадлежит Ж. Вокулеру [26]. Как видно из рис. 8, семейства спиральных галактик характеризуются буквами А, В, АВ. Здесь SА означает нормальную спиральную галактику, SB — спираль с перемычкой (баром), SAB — переходные формы. Кроме семейств, учитываются разновидности (кольцевая — r, спиральная — s, смешанная — rs).
Отметим, что спиральная конструкция обладает поворотной симметрией, порядок которой соответствует числу ветвей галактики.
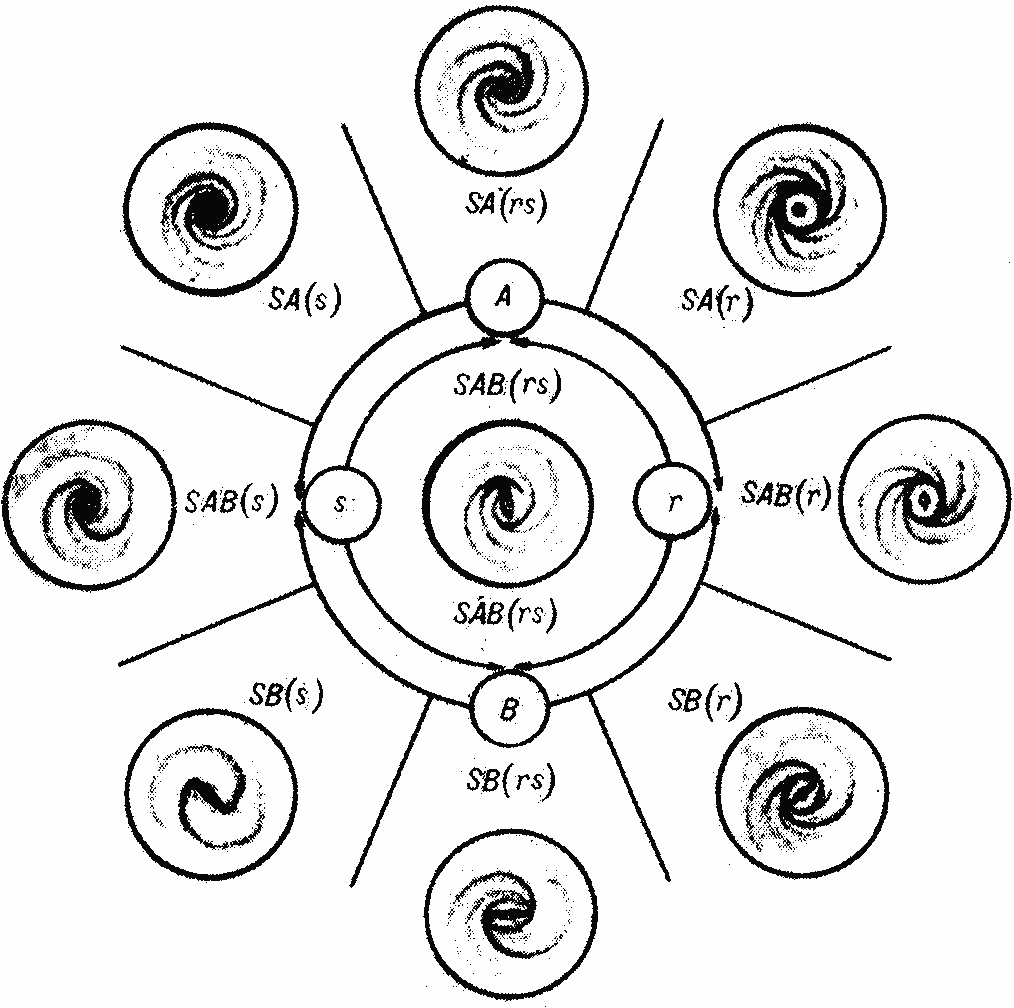
Рис. 8. Классификация спиральных галактик по Ж. Вокулеру
Представленные узоры подсказывают нам структуру потоков, некогда существовавших в оболочках протоядер галактик. Мы видим, что при слабом выделении энергии в недрах протоядер для выноса тепла из их экваториальных зон к полюсам было достаточно двух вращающихся “жгутов”. Но с увеличением мощности внутриядерного источника энергии число циркуляционных контуров возрастает. Естественно, при этом увеличивается скорость вращения объекта. В результате взрыва многожгутовая ротационно-диссипативная структура, отделившись от небесного тела, превращается в многоветвистую спиральную галактику, вращающуюся в космическом пространстве.
Внешний вид центральной части галактик зависит от гидродинамической ситуации, складывавшейся в глубинах протоядер. К обсуждению этого вопроса мы еще вернемся после анализа опытных данных.

