ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ ПРОЦЕССОВ КИПЕНИЯ И КОНДЕНСАЦИИ
До сих пор взаимодействие пара и жидкости рассматривалось нами как взаимное влияние энергетической природы, как средство обмена энергией в чистом виде. Перераспределение вещества между составными частями обеих подсистем — конденсационной и испарительной — нас интересовало лишь постольку, поскольку в ходе превращений между ними возникало деформационное взаимодействие.
Но в общем количестве энергии, содержащейся в паре, доля механической энергии незначительна. Как известно, теплота парообразования представляет собой сумму двух величин — внутренней потенциальной энергии тела (обозначим ее через ζ) и внешней работы расширения (Ψ)
В предыдущем разделе мы достаточно полно осветили вопрос о зависимости скорости передачи тепла от величины внешней теплоты парообразования Ψ. Теперь такую же ясность необходимо внести в отношении влияния на процесс величины ζ. Эта проблема заслуживает особого внимания, поэтому остановимся на ней более подробно.
Мы знаем, что представление о такой физической величине, как “энергия”, связывают с количеством движения материи. В частности, тепло есть не что иное, как количество движения частиц микромира (электронов, атомов, молекул). Следовательно, при теплообмене происходит обмен количеством движения между участвующими в процессе компонентами. Особенностью такой формы передачи энергии является рост энтропии, что, как полагают, отражает факт увеличения беспорядка в системе.
В подъемном канале испарителя мы наблюдаем явный рост энтропии. Для пояснения данного утверждения вновь привлечем понятия о конфигурационной и тепловой энтропиях, которые мы уже использовали в первом разделе нашего исследования. То, что казалось тогда нам сложным и непонятным в аналитической формулировке, в геометрической интерпретации становилось самоочевидным.
В данном случае будем считать, что возрастающее по высоте канала многообразие структур двухфазного потока отражает рост конфигурационной энтропии, а увеличение энтропии вторичного пара по отношению к энтропии вскипающей жидкости — рост тепловой энтропии. Условно можно принять, что за увеличение значений конфигурационной энтропии ответственна внешняя теплота парообразования, а тепловой — внутренняя.
Динамика изменения суммарной энтропии служит одной из важнейших координат состояния системы. Потенциалом взаимодействия, сопряженным с энтропией, является температура [139].
Напомним, что энтропия есть отношение приращения тепла, полученного в цикле, к абсолютной температуре. Как мы только что имели возможность убедиться, составители формулы (III.2), не мудрствуя лукаво, представляют коэффициент теплообмена при кипении как функцию приращения тепла во времени и таким способом косвенно вводят в рассмотрение изменение во времени энтропии.
Но для того, чтобы взять величину энтропии в качестве количественной характеристики скорости передачи тепла, необходимо быть уверенным в том, что температурный напор действительно определяет динамику процесса. Ситуация в подъемном канале испарителя, казалось бы, подтверждает незыблемость наших представлений о температуре, снижение которой приводит к росту энтропии.
Но иная картина складывается в конденсационном контуре. Здесь, несмотря на температурный напор, действующий в направлении от пара к стенке, энтропия системы в ходе процесса не увеличивается, а снижается, поскольку молекулы в конденсатной пленке располагаются более упорядоченно, чем в паре.
Экспериментально также установлено, что при равных температурных напорах интенсивность теплообмена, например, в испарителях, обогреваемых парами высокотемпературных органических теплоносителей (дифенильной смесью), в пять-шесть раз ниже, чем при обогреве водяным паром. Это обстоятельство повлекло за собой, в частности, необходимость введения в нормы расчета испарителей со стекающей пленкой сугубо индивидуальных критериальных зависимостей для каждого конкретного случая теплообмена [50, 140, 141].
Из изложенного следует, что для открытых систем температура не может служить потенциалом взаимодействия компонентов и, следовательно, энтропия не является количественной характеристикой переходных процессов. Увеличение или уменьшение беспорядка, отражаемое энтропией, есть следствие развития динамических процессов, протекающих в системе, а следствие не может стать причиной и тем более количественно определять скорость передачи тепла. Цепочка логических заключений приводит нас к мысли о том, что в арсенале термодинамики должна быть величина, более полно, чем температура, характеризующая интенсивность передачи энергии в открытых системах.
Действительно, для систем, где происходит обмен энергией и веществом, таковой величиной является химический потенциал [142]. Изменение состояния открытой системы, обусловленное рассматриваемым видом взаимодействия, проявляется в виде перераспределения ее массы между отдельными фазами. Очевидно, именно масса (обозначаемая литерой m) — физическая величина, являющаяся количественной мерой изменения, претерпеваемого системой.
Таким образом, мы приходим к простой зависимости dGi = μdm. (III.15).
В нашем случае химическая энергия процесса dGi полностью переходит в тепловую, поэтому изменение массы во времени практически отражает скорость передачи тепла.
Нам осталось уточнить порядок определения величины μ.
Мы рассматриваем здесь фазовые переходы одного вещества — Н2О, поэтому значения химического потенциала для единицы массы практически совпадают со значением свободной энергии ΔGi.
В свою очередь, величины
можно вычислить, рассматривая испарение как химическую реакцию [41]
(III.16)
В отличие от
, которые мало зависят от температуры, 
очень сильно зависит от температуры Т, которая явно входит в соотношение (III.16). Если ради простоты предположить, что изменения энтальпии и энтропии постоянны, то можно графически представить зависимость ΔGi от ΔΗ и ΔS, как это сделано на рис. 26 на примере Н2О.
При высоких температурах TΔS0 больше, чем ΔΗ0, свободная энергия испарения отрицательна и испарение воды при парциальном давлении водяных паров 1 атм должно происходить самопроизвольно. При низких температурах
больше, чем 
, так что
положительно, и самопроизвольно осуществляется конденсация водяных паров. В точке кипения при 
равно нулю, и жидкая и парообразная вода находятся в равновесии.
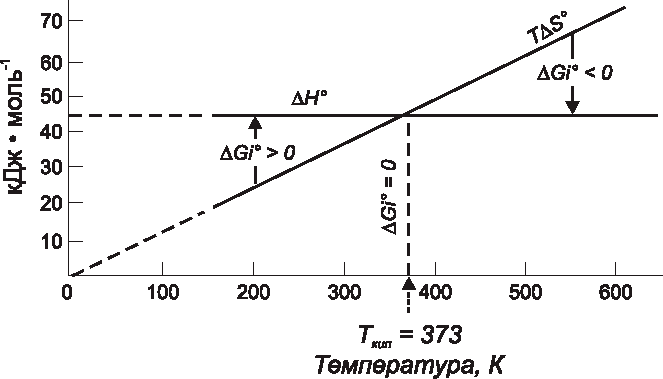
Рис. 26. Энтальпийный и энтропийный вклады в изменение свободной энергии испарения жидкой воды
Молярная теплота испарения может быть найдена как разность между стандартными теплотами образования жидкой и газообразной Н2О
Отсюда видно, что составители формул косвенно пытались применить термодинамический формализм при описании процесса теплообмена. Но даже в этом несовершенном с позиции термодинамики варианте представленные формулы позволяют установить определенную зависимость интенсивности теплообмена от гидродинамической обстановки на поверхности труб.
Поэтому, помимо замены r на μ, необходимо в последующих этапах расчета ввести еще две величины: поверхностное натяжение и геометрические параметры твердой поверхности. Далее, рассчитав значения поверхностной энергии Гиббса ΔGia, можно будет найти условия разрушения конденсатной пленки.
Не лучше обстоит дело с расчетом теплообмена при кипении. В псевдотермодинамическом варианте формула (III.2) выглядит как
(III.22)
Величина степени при r соответствует примерно тому значению, которое можно получить из второго приближения расчета испарителя, представив в открытом виде как функцию r.
Динамику изменения степени при r в переходном процессе можно проследить, воспользовавшись уравнением Ерофеева. Такую операцию, как вы помните, мы уже проводили при исследовании процесса испарения воды в горном озере.
Итак, с ростом Δt число центров парообразования (и, следовательно, степень при r) возрастает, достигает своего максимума в точке перегиба S-образной кривой, что соответствует приведенной выше зависимости, а затем, по мере оттеснения жидкости от стенки вторичным паром, падает. Таким образом, вариация степени при r отражает колебание величины поверхности контакта фаз в непосредственной близости от твердой стенки.
При оценке скорости процесса, как правило, стремятся ввести в расчеты измеряемые величины: температуру, давление, концентрацию. Так, например, Льюис и Рендалл предложили вместо химического потенциала применять термодинамическую активность, которую можно рассматривать как исправленную концентрацию [143]. Метод вполне приемлем для гомогенных систем. Но при фазовых превращениях, как мы только что смогли убедиться, возникает такая трудновычисляемая переменная величина, как поверхность контакта фаз.
К тому же в химических реакциях, к изучению которых мы сейчас приступаем, образующийся газ непрерывно отводится из зоны взаимодействия. Последнее обстоятельство не позволяет достичь равновесных условий, и поэтому давление газа (или его концентрация) не может быть рассчитано по энергии Гиббса. Все это не позволяет воспользоваться рекомендациями Льюса и Рендалла.
Подытожим данный раздел исследований. На основе анализа процесса испарения можно дать ряд рекомендаций, относящихся к последовательности обобщения опытных данных и расчета реакций взаимодействия сплавов с водой.
При низких давлениях возможен расчет скорости теплообмена образцов сплавов с водой на основе оценки ступенчатого процесса адиабатного вскипания воды. По найденной скорости отвода тепла несложно затем найти скорость реакции. В случае если величина реакционной поверхности неизвестна, опытные данные следует обобщать по уравнению Ерофеева. После нахождения оптимальных условий, соответствующих точкам перегиба S-образных кривых, где реакционная поверхность примерно равна начальной поверхности твердой фазы, необходимо представить опытные данные через химические потенциалы. Причем этот этап обобщения особенно необходим при высоких давлениях, когда вскипание воды невозможно и гидродинамическую обстановку в системе создает газ (водород), выделяющийся во время реакции.
В ходе процесса величины энергии Гиббса претерпевают соответствующие изменения. Поэтому, приняв для оценки значений μ равновесные величины энергии Гиббса, мы тем самым переводим выполняемый расчет в разряд приближенных. Более точные данные можно получить, выполнив ряд последующих итераций.
