Нам предстоит познакомиться в этом разделе с достаточно сложной проблемой — оценкой скорости топохимических реакций. Ряд исследователей полагает, что роль концентрации в этих системах выполняет величина реакционной поверхности. Отсюда скорость реакции, по их мнению, зависит от того, насколько развита реакционная поверхность. Но это всего лишь один из факторов, влияющих на процесс.
Скорость реакции является результатом воздействия: располагаемого энергетического потенциала, свойств сплавов и воды, поверхности контакта фаз и газогидродинамической обстановки внутри аппарата.
Постараемся упорядочить наши представления о процессе, рассмотрев реакции взаимодействия сплавов алюминия и кремния с водой.
3.3.1. Взаимодействие активированного алюминия с водой
Производство водорода в автономных условиях получило наиболее широкое распространение в системе гидрометеослужбы.
По данным Всемирной метеорологической организации (WMO), в большинстве стран водород генерируют непосредственно на метеостанциях. Основной способ получения водорода — реакция взаимодействия сплавов с водным раствором едкого натра [144].
В перспективе в связи с непрерывным увеличением стоимости углеводородного сырья вода будет главным источником получения водорода. Высокая калорийность и отсутствие вредных веществ в продуктах сгорания определяют значительные преимущества водорода по сравнению с другими видами топлива. Вполне возможно, что применяемая в настоящее время на метеостанциях технология является прообразом тех многотоннажных производств водорода, которые в недалеком будущем займут свое достойное место в промышленности высокоразвитых стран. По этой причине не снижается интерес к исследованию закономерностей взаимодействия сплавов с водой. Для описания явления во всей полноте приходится прибегать как к методам термодинамики, так и к смежным дисциплинам, трактующим процесс с точки зрения кинетики. В данной работе ставится задача выявить роль тепломассообмена в ходе химических и физических превращений сплавов в оксиды.
В качестве предмета исследования выбрана реакция взаимодействия алюминия с водой
![]() (III.23)
(III.23)
Необходимо установить скорость и полноту данной реакции.
Равновесные характеристики процесса исследованы достаточно подробно. Известно, что при температуре 363 К энергия Гиббса имеет величину ΔGi = —927,2 кДж, а константа равновесия достигает значения К = 2,66·10133. Значительные отрицательные величины ΔGi свидетельствуют о высокой вероятности реакции. Полнота реакции, рассчитанная по константе равновесия, практически близка к единице. При адиабатном ведении процесса в зоне реакции развивается температура 2880 К, в то время как 5-кратный избыток воды по отношению к стехиометрическому объему снижает температуру до 760 К [145]. На данный момент представления о скорости реакции менее четкие. При умеренных температурах чистый алюминий покрыт плотной оксидной пленкой и практически не взаимодействует с водой [146]. В тоже время ряд сплавов алюминия в тех же условиях проявляет исключительно высокую активность. Так, например, скорость вытеснения водорода из воды сплавом АГ5О5И5 (масс. %: А — 85, Ga — 5, Sn — 5, In — 5) более чем на два порядка превышает скорость вытеснения водорода алюмокремниевыми сплавами [147, 148].
В общем случае скорость реакции зависит от структуры и состава сплава, свойств воды и образующегося оксидного слоя, температуры, давления, формы и размеров реагирующей системы, а также свойств контактирующей с ней части окружающей среды. Тем не менее, существуют некоторые определяющие факторы, дающие право говорить о возможности расчета предельной скорости процесса, достижимой при прочих благоприятных условиях.
К числу таких факторов относится, в частности, местная скорость звука, ограничивающая скорость истечения водорода из зон образования ядер оксидов. Но для оценки производительности реактора необходимо знать, кроме того, число и площадь сечения зон выделения газа, приходящихся на единицу площади поверхности сплава. Определение величины реакционной поверхности, изменяющейся в ходе процесса, — задача трудновыполнимая, поэтому целесообразно обратить основное внимание на теплообмен.
Тепло способно “растекаться” в твердом теле, что в первом приближении позволяет принимать площадь поверхности теплообмена равной площади поверхности образца сплава.
В результате газообразования объем реагирующей системы увеличивается в сотни раз, что обуславливает возникновение естественной циркуляции воды вблизи реагирующей поверхности. Скорость подъемного потока также ограничена местной скоростью звука.
Установление величин температурного напора и скорости омывания образца жидкостью позволяет по обычным критериальным зависимостям рассчитать интенсивность теплообмена. Зная удельный тепловой поток, несложно подсчитать эквивалентный ему массовый поток водорода. Тем самым открывается возможность предварительного расчета предельно достижимой скорости газовыделения. Такой подход справедлив, если допустить, что химическая стадия процесса имеет минимальное сопротивление. Следовательно, сопротивление физической стадии, обусловленное подводом воды и удалением продуктов реакции и тепла, определяет скорость реакции.
Опыты по изучению тепломассобмена проведены в стеклянном аппарате Киппа и металлическом реакторе [50]. Исследована интенсивность теплоотдачи от кубиков, изготовленных из сплавов АГ5О5И5 и ФСА, к циркулирующему потоку.
В центре кубика со стороной (10-25)-10-3 м устанавливают термопару. Отверстие для термопары (dотв = 3·10-3 м) заливают эпоксидной смолой, предварительно изолировав спай термопары от эпоксидной смолы слоем хлопка. Контакт между термопарой и телом кубика контролируют тестером. В качестве вторичного прибора используют потенциометр типа КСП-4 и зеркальный потенциометр КП-59.
Одновременно с записью температуры среды фиксируют температуру центра образца. Измерение температуры поверхности образца выполняют термопарой со щупом при проведении реакции в открытом сосуде.
Инерционность системы проверяют по ранее принятому способу [149].
Образцы имели начальную площадь поверхности (1,4-1,8)-10-3 м2.
Давление в реакторе не превышало 0,94 МПа. Максимальная скорость выделения водорода при этом составила Wmax = 1,05·10-3 м3/(кг-с) или Wmax = 7,14·10-3 м3/(м2-с).
При исследовании реакции в открытом сосуде установлено, что температура внешней поверхности гидрооксидного слоя в местах газообразования (tm) выше температуры среды (td) на 1,6-2,4 °С. Температура центра образца (tц) превышает температуры среды на 2,4-6,2 °С (рис. 27).
Приближение фронта реакции к спаю термопары в центре образца вызывает скачкообразное повышение температуры на 5-9 °С при кипении и газообразовании (аппарат Киппа) и на 37-53 °С при одном газообразовании (закрытый реактор). Больший скачок наблюдается при более высокой температуре. Время прохождения всплеска температуры — 10-15 секунд. При извлечении образца температура внешней поверхности (tm) быстро повышается и затем падает. Это объясняется тем, что некоторое время реакция продолжается за счет воды, оставшейся на поверхности.
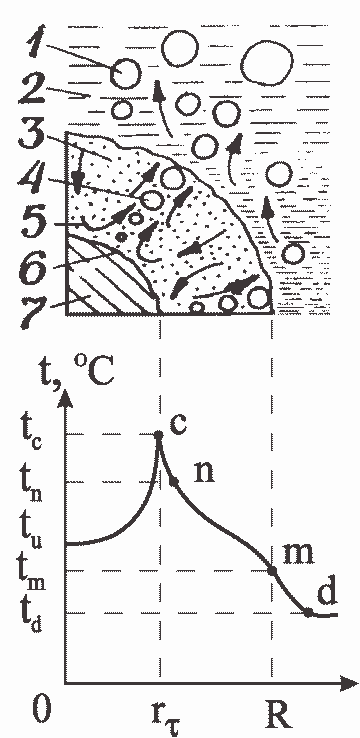
Рис. 27. Схема частицы сплава и изменения ее температуры при взаимодействии с водой
2 — газовые пузыри в жидкости; 2 — жидкость; 3 — слой образующегося гидрооксида; 4 — газовые пузыри в слое гидрооксида; 5 — направление циркулирующих потоков жидкости в слое гидрооксида; 6 — реакционная поверхность частицы; 7 — непрореагировавшее ядро частицы.
После прохождения скачка прибор показывает температуру среды (измеряемую дополнительно ртутным термометром), что свидетельствует о завершении реакции в связи с полным разрушением образца. Динамика роста температуры центра образца при падении кубика в воду в кинетическом реакторе отражена на рис. 28. На начальном этапе температура резко возрастает, затем темп роста замедляется, тем самым сказывается влияние образующегося оксидного слоя. Разрушение и осыпание образца во время реакции вызывает повышение температуры на дне реактора.
Величина температуры границы между алюминием и раскаленным оксидом алюминия говорит о том, что на поверхности контакта происходит вскипание воды.
Экспериментальные значения температуры реакционной поверхности (tn) с учетом принятой инерционности системы оказались равными температуре кипящей жидкости при критическом давлении истечения газового потока. Так, на конечной стадии реакции за 15 с температура поднялась со 102 °С до 114 °С (рис. 28). Ввиду кратковременности существования тонкого реагирующего слоя и значительной инерционности системы измерения реальная величина температуры составляет 194 °С. Фактический скачок — 92 °С. В пересчете на полупериод реакции (τ0,5 = 330 с) подъем температуры происходит от 90 °Сдо 173 °С, т.е. всплеск составляет 83 °С. Величина 173 °С является температурой насыщения при критическом давлении истечения потока, зафиксированном в момент времени, соответствующий τ0,5.
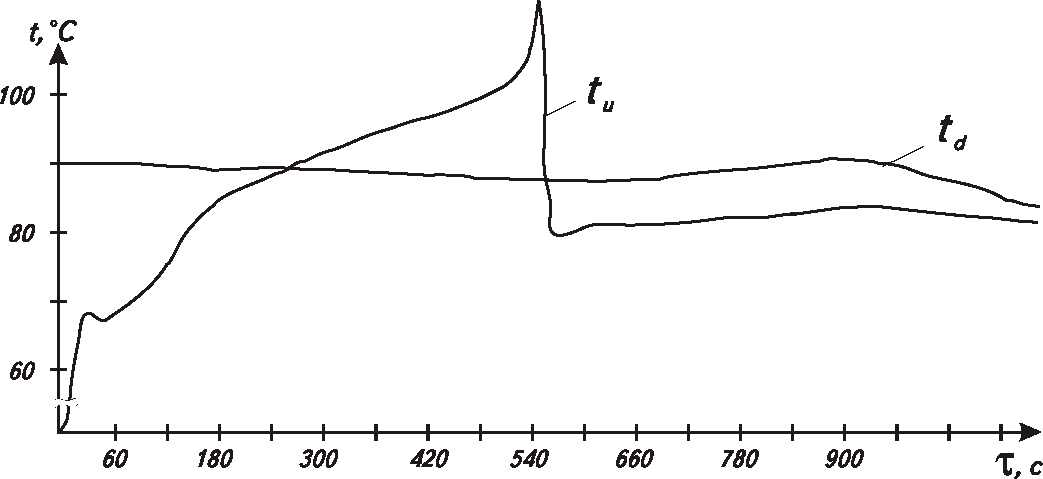
Рис. 28. Изменение температуры в зависимости от времени при реакции сплава АГ505И5 с водой (кинетический стенд), tн = 90 °С
tц - центр образца; td — дно реактора; m - 11,8·103 кг.
Установленные величины температур реакционной поверхности сплава АГ5О5И5 позволяют рассчитать среднелогарифмический температурный напор, обеспечивающий передачу тепла. При этом Δtmax = tn — td, а Δtmin = 2+3 °С (см. рис. 28).
Естественная циркуляция обеспечивает послойное взаимодействие частицы с омывающей ее жидкостью. Скорость обтекания частицы равна приведенной скорости жидкости vпр в подъемном канале. Для нахождения vпр проводят оценку гидродинамики циркулирующего потока. При низком давлении течение в подъемном потоке определяет пар, а с повышением давления — водород. В начальный момент скорость потока находят по изменению энтальпии вскипающей жидкости [50]. Во втором случае используют формулы для оценки местной скорости звука в двухфазном потоке [150]. При этом учитывают не только стехиометрические количества продуктов реакции, но и объем воды, испарившейся на реакционной поверхности и сконденсировавшейся в подъемном потоке. Средняя скорость потока равна 2/3 величины скорости истечения. Найденное значение средней скорости позволяет уточнить количество поднимаемой жидкости по зависимостям для газлифтов [151, 152].
![]() (III.24)
(III.24)
где φ — газосодержание; μж — вязкость жидкости, МПа-с; dп.п. — диаметр подъемного канала, м; vг.пр — приведенная скорость течения газа, м/с.
Использование данных [151] позволило установить, что правую часть уравнения необходимо умножить на коэффициент kэ, изменяющийся в пределах 0,292+0,753. Снижение kэ наблюдается при уменьшении диаметра подъемного потока, который принят равным сумме диаметров частицы и двух пузырьков [153]. Для рассматриваемых нами условий k э = 0,333.
Значение приведенной скорости жидкости, найденное по разработанной методике, находится в пределах 1,81+2,1 м/с. Числа Рейнольдса изменяются от 45626 до 110891. Поскольку коэффициент лобового сопротивления kлс в указанном интервале возрастает [154], следует ожидать увеличения безразмерного коэффициента теплоотдачи с ростом чисел Рейнольдса.
Экспериментальные данные обработаны по известным зависимостям. Расчеты выполнены на момент времени t0,5. Оказалось, что наименьшие отклонения дает формула Кунии, а наибольшие — формула Кацнельсона—Тимофеевой [155]. В упомянутых работах степень влияния чисел Reнаходится в пределах 0,5+0,58. При омывании реагирующей частицы обнаружено более существенное влияние критерия Рейнольдса.
![]() (III.25)
(III.25)
Отклонение расчетных значений критерия Nu от опытных не превышает 13,5 %.
С ростом скорости омывания возрастает паро- и газообразование, что сопровождается турбулизацией пограничного слоя. Близкие условия тепломассообмена наблюдаются при испарении воды в собственные перегретые пары [157].
Из сказанного следует, что в условиях гетерогенной системы предельное значение скорости химической реакции определяется интенсивностью теплоотдачи при естественной циркуляции [158]. Полученные результаты позволяют выделить два основных фактора, определяющих скорость реакции.
Во-первых, при сопряжении основной экзотермической реакции (образование водорода) с параллельной эндотермической (вскипание воды) процесс идет при малых температурных напорах, т.е. в условиях, близких к равновесию второй реакции.
Во-вторых, в гетерогенной системе взаимодействующие компоненты реагируют послойно [159].
Оба указанных выше фактора обеспечивают сравнительно низкие скорости течения 3-фазного потока, т.е. затраты на трение ничтожны. Известно, что КПД вскипающей системы не превышает 0,25 %, т.е. всего четвертая часть процента передаваемого через систему тепла преобразуется в механическую энергию [50]. С повышением давления в кинетическую энергию циркулирующего потока (диссипативной структуры) [36] преобразуются сотые доли процента химической энергии, что соответствует минимальному производству энтропии за счет трения [160].
Продолжим исследование процесса взаимодействия сплава алюминия с водой.
На этот раз в качестве объекта исследования возьмем реакцию взаимодействия множества частиц активированного алюминия (порошка) с водой. В этом процессе температурные и гидродинамические условия, возникающие на поверхности одной отдельной частицы, оказывают существенное влияние на развитие реакции воды с соседними частицами.
Здесь мы снова сталкиваемся с коллективными явлениями, на которых кратко останавливались в первом разделе. Как мы уже знаем, наиболее удобной формой обобщения опытных данных в этом случае является уравнение Ерофеева.
Познакомимся с работами, приведшими к такому заключению. Но прежде всего отметим ряд исследований, внесших заметный вклад в развитие теории гетерогенных реакций.
Модели топохимических реакций разрабатывались с учетом геометрических и энергетических характеристик системы.
Основными факторами, определяющими место образования зародышей на поверхности частиц, являются вероятность захвата и возможность выделения газообразных продуктов. Выражение доли прореагировавшего вещества учитывает оба этих фактора и может быть решено только приближенно. Однако для случайного распределения Аврами [161] решил уравнение, используя понятие о расширенном объеме прореагировавшего вещества. Принятое допущение оказалось справедливым лишь для умеренных превращений. Мампель [162] рассмотрел процесс образования ядер и их рост в системах, состоящих из шарообразных микрокристаллов. Влияние предложенной модели на развитие теории процесса оказалось незначительным ввиду трудностей приготовления образцов, на которых возможна ее проверка. Праут и Томпкинс [163] учли возможность образования зародышей в цепном процессе и предложили свое обобщающее уравнение. Болдырев [164] объяснил влияние примесей на кинетику процесса зародышеобразования, во-первых, деформационным действием решетки включения на пограничный слой основного вещества и, во-вторых, изменением характера электронных и ионных процессов, протекающих на границе раздела примесь-исходное вещество. Янг [165] разделил реакции разложения на два подкласса. В одном подклассе цепная разветвленная реакция проходит только на поверхности кристалла, при этом в точках разветвления образуются компактные объемные ядра, в другом — характерно растрескивание кристалла, вызванное проникновением реакции в объем исходного вещества. Дельмон [166] развил подход, предложенный Мампелем, и рассмотрел кинетические характеристики взаимодействия газа с твердым телом, включая последующую диффузию. Для многих важных кинетических задач Дельмон дал численные решения и привел табличные данные. Барре [167] сделал обзор работ по кинетике гетерогенных реакций, уделяя особое внимание физическому смыслу констант, входящих в математические зависимости. Розовский [168] построил ряд теоретических моделей и дал численные решения применительно к конкретным реакциям. Браун и др. [169] рекомендовали интервалы применимости и корректности известных кинетических уравнений реакций взаимодействия и термического разложения. Отмечено, что большинство зависимостей неудовлетворительно описывает конечную стадию процесса. Это связывают с одновременным влиянием таких факторов, как размер частиц, фрагментация кристаллитов, хемсорбия газообразных продуктов на твердом остатке, отравление и т.д.
Ерофеев [42], анализируя вероятность взаимодействия молекул данной системы, получил уравнение (I.1), о котором у нас уже шла речь ранее.
В работах [159, 165, 169, 170] высказано мнение, что уравнение (I.1) наиболее полно отражает формальную кинетику процесса.
Таким образом, мы не сделаем большой ошибки, обобщая опытные данные по уравнению Ерофеева.
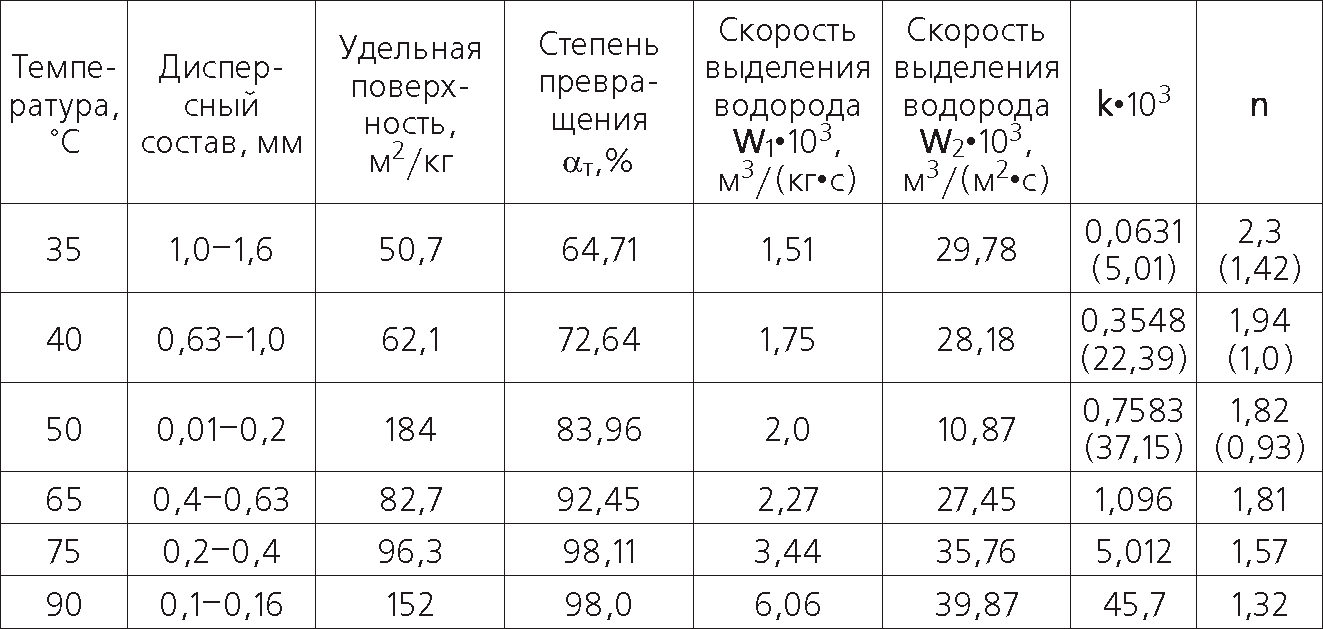
В координатах α—τ кинетика описывается типичными сигмоидными кривыми, практически отражающими изменение величины реакционной поверхности во времени (рис. 7). В логарифмических координатах опытные данные представлены на рис. 29, расчетные значения n и k указаны в табл. 1. С повышением температуры значения k возрастают, а n — уменьшаются. Разброс экспериментальных точек при высоких температурах усиливается, следовательно, уравнение Ерофеева лишь приближенно описывает процесс. В конце реакции константа скорости возрастает в 49,2—79,5 раза, а показатель n снижается в 1,6—2,0 раза, что вызвано диффузионным торможением процесса из-за накапливающихся на поверхности сплава твердых продуктов реакции. Сравнение с данными Ле- пинь [43] показывает, что характер реакции изучаемого сплава с водой во времени (показатель n) сохраняется таким же, как и для чистого алюминия. Однако в случае активированного алюминия константа скорости k при температуре 40 °С на четыре, а при 70 °С — на два порядка выше, чем у чистого алюминия. Это свидетельствует о различной природе рассматриваемых веществ. В частности, подтверждается то обстоятельство, что развитие реакционной поверхности в образце активированного алюминия с мелкозернистой структурой происходит за счет его растрескивания.
На основании проведенных исследований был создан более эффективный сплав [171].
Кинетика взаимодействия этого сплава с водой раскрыта в работе [172].
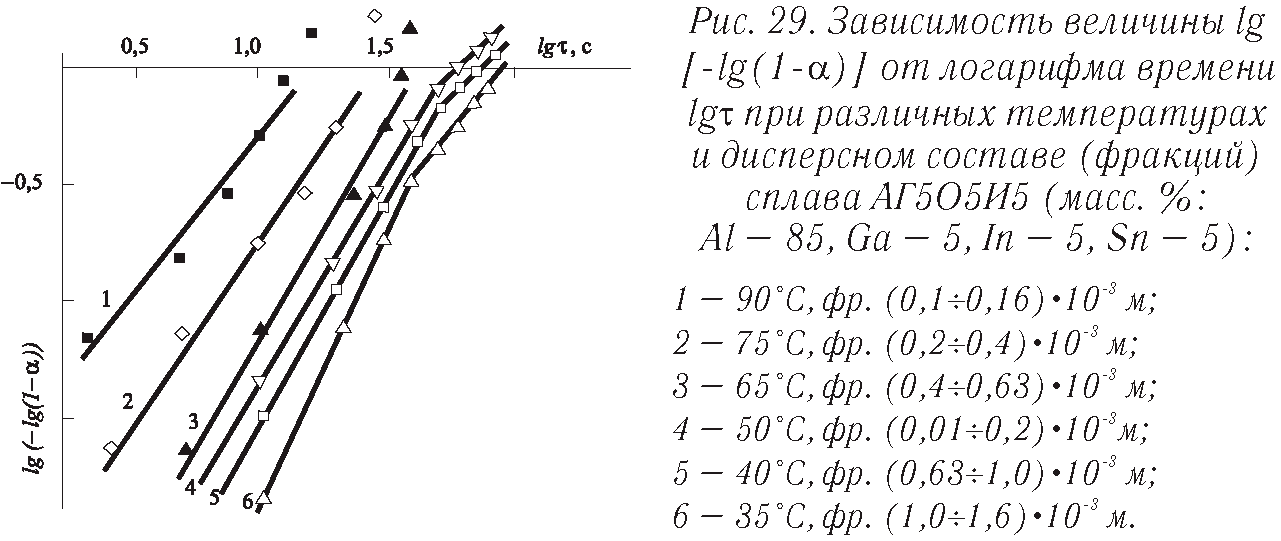
Таблица 1
Зависимость степени превращения (αт, %) и скорости выделения водорода от температуры и дисперсного состава активированного алюминия (5 % Ga, 5 % In, 5 % Sn)