ГЛАВА 3
ФАЗОВЫЕ И ХИМИЧЕСКИЕ ПРЕВРАЩЕНИЯ В НЕДРАХ ЗЕМЛИ
Итак, мы подошли к решению одной из главных целей нашего исследования — оценке мощности подземных источников тепла и определении скорости выделения ими этой энергии.
Но прежде чем приступить к намеченным расчетам, нам необходимо выявить наиболее важные методы и средства, которыми располагает термодинамика, и показать ход применения этих методов для расчета интенсивности теплообмена при фазовых и химических превращениях.
В качестве примера фазовых превращений возьмем процесс, наблюдаемый в испарителях с поднимающейся пленкой.
3.1. ТЕПЛООБМЕН В ИСПАРИТЕЛЕ С ПОДНИМАЮЩЕЙСЯ ПЛЕНКОЙ
Как правило, для описания теплообмена при кипении и конденсации в качестве независимой переменной принимают температурный напор. В связи с этим возникает явное противоречие между наблюдаемой интенсивностью теплообмена и способом обобщения опытных данных.
Так, известно, что плотность теплового потока при любых видах теплообмена пропорциональна установленной разности температур. Между тем, при кипении и конденсации температурные различия между фазами могут быть сколь угодно малыми, но интенсивность теплообмена в большинстве случаев многократно превышает наблюдаемую для конвективного теплообмена.
К числу недостатков известных методов расчета испарителей, конденсаторов и парогенераторов относится введение в зависимости для коэффициентов теплоотдачи неизвестных величин, таких, как температурный напор и удельная тепловая нагрузка.
В этом можно убедиться при анализе, например, уравнения Нуссельта для конденсации насыщенного пара любого вещества при стекании пленки конденсата по стенкам вертикальных труб [129, 130]*:
(III.1)
* Возможно, у читателя не окажется под рукой первой части книги, поэтому автор приводит здесь обозначения величин.
где а — среднее значение коэффициента теплоотдачи;
r — теплота конденсации, Дж/кг;
р — плотность конденсата, кг/м3;
λ — теплопроводность конденсата, Вт/(м-°С);
μ — динамический коэффициент вязкости конденсата, кг/(м-с);
Н — высота вертикальной трубы, м;
Δ t — разность температур, °С;
g — ускорение свободного падения, м/с2.
Предпосылки при выводе формулы (III.1) таковы: течение пленки конденсата имеет ламинарный характер; силы инерции, возникающие в пленке, пренебрежимо малы по сравнению с силами вязкости и веса; сила тяжести единичного объема конденсата уравновешивается силой вязкости, действующей со стороны соседних слоев жидкости; конвективный перенос тепла в пленке, а также теплопроводность вдоль нее малы по сравнению с теплопроводностью поперек пленки; трение конденсата о пар отсутствует, температура внешней поверхности пленки равна температуре насыщенного пара; плотность и коэффициенты теплопроводности и вязкости конденсата от температуры не зависят.
Из уравнения (III.1) следует, что средний коэффициент теплоотдачи уменьшается с ростом высоты H теплообменных труб испарителя и температурного напора. В точных расчетах учитывают волновой режим течения пленки и изменение физических свойств конденсата в зависимости от температуры.
Учет последних двух поправок не устраняет главного недостатка формулы, а именно: остается неизвестной величина Δt. Кроме того, приведенная выше зависимость справедлива для неподвижного пара или когда скорость его течения мала. В нагревательных камерах типовых испарителей скорость движения пара как в продольном, так и в поперечном направлениях через пучок труб к центру достаточно высока. В этом случае поток пара оказывает динамическое воздействие на конденсатную пленку.
В длиннотрубных испарителях температура пара (в состоянии насыщения) снижается от зоны ввода пара в верхней части аппаратов до места выхода конденсата вблизи нижней трубной решетки примерно на 2—3 °С. В пучке труб также имеется определенный перепад температур по сечению аппарата. Этот фактор необходимо учитывать в расчетах.
Примерно такая же ситуация неопределенности сложилась в случае использования известных формул для расчета теплоотдачи при кипении. Поскольку объем образующегося при кипении пара в сотни раз больше объема испаряемой жидкости, то при отводе пара от теплоотдающей поверхности возникает интенсивная турбулизация пристенного слоя. Это обстоятельство учитывают введением экспериментальных значений удельной тепловой нагрузки q в расчетные зависимости коэффициентов теплоотдачи а. В частности, распространенной является степенная зависимость вида [131] 
(III.2) где с — коэффициент пропорциональности, величина которого зависит от рода жидкости и давления, а также в некоторой степени от поверхностных условий.
Изложенный прием оценки интенсивности теплоотдачи содержит в себе явное противоречие, поскольку если известно значение q, то для выбора поверхности теплопередачи практически нет необходимости рассчитывать а.
Противоречия исключаются при рассмотрении процессов кипения и конденсации на основе термодинамических закономерностей. В качестве примера рассмотрим последовательность расчета испарителей с поднимающейся (или восходящей) пленкой. Конструктивно эти аппараты выполняют таким образом, что конденсирующийся поток движется в низ межтрубного пространства, как это происходит у испарителей со стекающей пленкой, а испаряемый — в верх трубного пространства [132]. Причем первое пространство входит в состав конденсационного контура, а второе — испарительного.
Оба контура представляют собой проточные системы, обмен энергией между которыми в виде тепла сопровождается перераспределением вещества между составными частями циркулируемых потоков. Последнее обстоятельство приводит к возникновению деформационного взаимодействия между фазами каждой системы, что дает возможность рассматривать циркуляционные контуры как тепловые двигатели, обеспечивающие определенную скорость течения потоков вдоль теплообменной поверхности аппарата.
Данному факту следует придать должную отчетливость, достаточную для того, чтобы решить вопрос о скорости передачи тепла при фазовых превращениях. С этой целью необходимо выполнить анализ сложной физической ситуации и осмыслить под определенным углом зрения множество разрозненных, внешне между собой не связанных результатов опыта.
Экспериментально наблюдаемая гидродинамическая обстановка в отдельно взятой теплопередающей трубе представлена на рис. 23. На рис. 24 даны профили изменения температуры потока и стенки обогреваемой трубы [133]. Как видим, перед закипанием исходный поток повышает свою температуру на несколько градусов. Объясняется этот эффект тем, что в зоне закипания раствора создается повышенное давление вторичного пара, что необходимо для преодоления им сопротивления канала течению двухфазного потока.
Рис. 23. Структура потока при кипении жидкости внутри вертикальной трубы
Участки потока: bc — однофазный; cj — эмульсионный; jf — пробковый; fu — стержневой.
Рис. 24. Изменение температур по высоте теплопередающей трубы
1 — потока; 2 — стенки трубы.
По мере продвижения кипящего потока внутри канала эмульсионный режим течения сменяется пробковым, а затем — стержневым.
Одновременно вторичный пар, поднимая жидкость на определенную высоту, делает запас работы гравитационного поля. Этот запас после отвода пара гравитационное поле использует для опускания жидкости.
В межтрубном пространстве складывается следующая гидродинамическая ситуация. Здесь первичный пар, конденсируясь, формирует пленку конденсата на внешней поверхности испарительных труб, чем опять же делается запас работы гравитационного поля. Используя этот запас, гравитационное поле вынуждает конденсатную пленку стекать в низ нагревательной камеры. Причем толщина стекающей пленки возрастает к низу трубы по мере конденсации очередных порций первичного пара. Поток первичного пара, двигаясь в том же направлении, ускоряет течение конденсатной пленки.
В соответствии с аналогией Рейнольдса, устанавливающей определенную зависимость между сопротивлением каналов течению потоков и интенсивностью передачи тепла, следует ожидать различных значений коэффициентов теплоотдачи по высоте испарительных труб.
Для оценки локальных значений коэффициентов теплоотдачи представим процессы, протекающие в каналах испарителя, в виде бинарного цикла в системе координат T—S(рис. 25). При этом сопряжение циклов выполним таким образом, чтобы процесс адиабатического расширения первичного пара в начале межтрубного пространства (линия meze), находился над точкой окончания процесса адиабатного вскипания раствора в выходном участке нагревательной трубы (точка zi).
Температура пара, поступающего от тепловой станции, как правило, превышает ту, что необходима для испарителя. В связи с этим первичный пар перед подачей в межтрубное пространство предварительно увлажняют. Для этого перед испарителем устанавливают редукционно-охладительную установку (РОУ) [134, 135].
Отсюда следует, что предыдущее условие, касающееся размещения циклов, легко выполняется подбором соответствующего влагосодержания первичного пара. Принятый для наглядности способ совмещения циклов испарения и конденсации должен тем не менее подчиняться общему принципу — неизменности значений теплового потока, проходящего через различные среды (см. уравнение III.4).
Рис. 25. Бинарный цикл испарительной установки в системе координат T—S
Итак, площадь верхней ступени бинарного цикла, ограниченная линией aebenemezeceae, соответствует количеству тепла, преобразуемого в работу, выполняемую первичным паром по ускорению течения конденсатной пленки.
В свою очередь, часть тепловой энергии, ограниченная на Т—S диаграмме площадью фигуры aibiciuiziai, преобразуется в испарительном контуре в механическую энергию, затрачиваемую на циркуляцию кипящего потока.
Сравнивая форму обеих фигур, отмечаем, что профиль линии biciui, отражающей ход изменения температуры кипящего раствора по высоте нагревательной трубы, примерно соответствует профилю линии aeceze, фиксирующей вариацию температуры пленки конденсата, стекающей снаружи той же трубы.
Площадь, заключенная между этими линиями, численно равняется потере работоспособности системы в связи со снижением температуры в конденсатной пленке, стенке труб и пограничном слое раствора.
Диаграммы верхней и нижней ступеней отражают работу, совершаемую упругими рабочими телами — первичным и вторичным водяным паром при своем расширении в продольном направлении.
Что касается работы гравитационного поля в опускном канале испарителя и в межтрубном пространстве при стекании конденсатной пленки, то изменения температур жидкости в том и другом случаях будут крайне незначительны.
Известно, что если масса m опускается на расстояние L при ускорении силы тяжести g, то уменьшение гравитационной энергии на mgL равно увеличению кинетической энергии на
, где V — скорость. Если перепад высот L выразить в м, то L будет также располагаемой работой, например 1 кг воды в кгм. Предположим, что в результате трения потоков о стенки труб располагаемая работа полностью переходит в тепло. Тогда при Н = 10 м повышение температуры 1 кг воды состоится на величину
Разобьем дальнейший свой расчет на три последовательных этапа. В первом приближении найдем коэффициенты теплопередачи от неподвижного обогревающего пара к раствору, а во втором — учтем ускорение конденсатной пленки потоком пара.
В третьем, наиболее сложном, этапе обоснуем и новый вид расчетных зависимостей.
Вначале воспользуемся методикой расчета скорости естественной циркуляции, изложенной в первой части данной книги.
Для этого предположим, что “срабатывает” лишь температурный напор, действующий в продольном направлении по высоте теплообменных труб. На диаграмме Т—S адиабатный процесс вскипания изображен вертикальной линией cd (рис. 4 Ч.I). Найденному значению скорости потока vсоответствует определенная интенсивность отдачи тепла, рассчитываемая по зависимости для конвективного теплообмена [131].
По найденным значениям скорости течения потока определяют распределение температурных напоров между обогревающим паром и испаряемой жидкостью.
Общий температурный напор
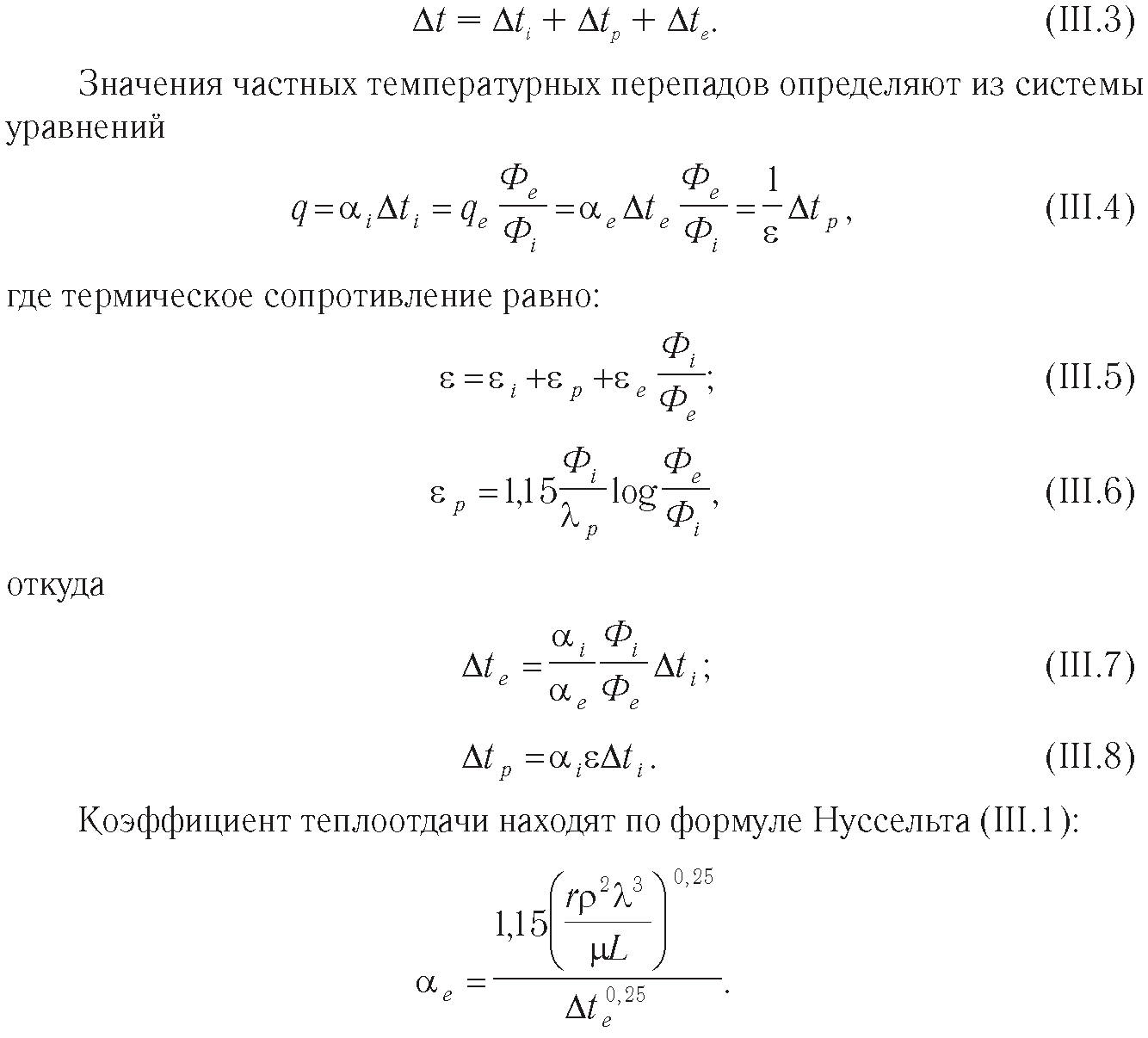
Здесь r принимают при te; p, μ, λ для конденсатной пленки определяют при температуре конденсации tкон, которую первоначально задают по зависимости
где при расчете критерия Re используют значения скорости циркуляции, найденные из термодинамического расчета. После подстановки значения ai в уравнение (III.10) находят величину Δti, а затем — последовательно по зависимостям (III.8), (III.9) определяют значения Δtp и Δte. Значение величины Δte открывает возможность расчета aе, а затем и коэффициента теплопередачи.
Второй этап расчета — определение коэффициентов теплоотдачи при кипении — выполняют после анализа гидродинамической обстановки, возникающей в пристенном слое при установленном Δ ti.
По своей природе циркуляция кипящей жидкости в пристенном слое аналогична естественной циркуляции потока в аппарате. В связи с этим расчет кипения также проводится по диаграммам, приведенным на рис. 4. Ч.I. Отходящая от стенки жидкость (см. рис. 4. Ч.I) вскипает в процессе cd(cn— действительный процесс расширения потока). После отделения пара в центре трубки (процесс da) жидкость под воздействием гравитационного поля вновь опускается к стенке (процесс ab), где она нагревается, повышая свою температуру на величину Δti (процесс bc).
В стационарных условиях давление среды возле вертикальной теплопередающей стенки не изменяется. Однако если образовавшийся при кипении пар отходит от поверхности теплопередачи с определенной скоростью, то, согласно закону сохранения количества движения, давление у поверхности должно повыситься. Одновременно на пузырек начинает действовать масса вышележащих слоев жидкости, что обусловливает его движение по траектории под углом к оси трубки. Образование пузырьков — процесс периодический. В момент всплытия пузырьков давление возле стенки снижается, что дает возможность потоку жидкости, также обладающему некоторым скоростным напором, подойти из центральной зоны трубы к ее поверхности. Для продольного потока поступление в него пара от поперечного потока является практически изотермическим процессом, что изображается на Т—S диаграмме горизонтальными линиями.
Разбив теплообменную трубу по высоте на отдельные участки, как показано на рис. 25, мы, последовательно используя продольный и поперечный температурные напоры, приходим к действительной скорости течения. По этой скорости уточняем гидродинамический режим течения и значение ai, а затем, подсчитав установившиеся температурные напоры, окончательно находим aе. Расчет завершаем оценкой коэффициента теплопередачи [50].
Установлено, что при капельной конденсации aе существенно возрастает [136].
В этом случае при сравнительно небольших скоростях пара (vп = 4,5—13,3 м/с) коэффициент теплоотдачи aе увеличивается в 1,5—3,5 раза по сравнению со значениями для неподвижного пара. С увеличением скорости течения пара до vп = 19,5—67,2 м/с коэффициент теплоотдачи возрастает в 1,9—7,4 раза.
Причем коэффициент теплоотдачи при капельной конденсации с увеличением скорости пара растет более существенно, чем при пленочной. Так, при ламинарном течении пленки увеличение скорости течения пара с 19,4 до 44,7 м/с приводит к росту aе по сравнению с неподвижным паром всего лишь в 3,5 раза. Оценку скорости пара проводят с использованием Т—S диаграммы (рис. 25), где также рассматривают адиабатический процесс расширения.
Для перечисленных выше условий составлены соответствующие критериальные зависимости, применяемые в практических расчетах [137]. Перед оценкой поверхности теплопередачи в третьем приближении необходимо обсудить физико-химические основы процессов кипения и конденсации.
