Оптимизация электродных систем
Задача оптимизации электродных систем обычно заключается в определении формы и размеров электродов, при которых напряженность электрического поля была бы одновременно минимальной и постоянной по всей поверхности электродов.
Для простейших конфигураций электродных систем возможна их оптимизация в аналитическом виде, например для классических цилиндрического и сферического конденсаторов. Более сложные устройства можно оптимизировать только с помощью численных расчетов.
Аналитическая оптимизация
5.3.1.1. Цилиндрический конденсатор.
Большое практическое значение имеет вопрос, каким должен быть внутренний радиус r1 коаксиального устройства при значениях наружного радиуса r2 и приложенном напряжении U, чтобы напряженность электрического поля на внутреннем проводе была минимальной.
Эта напряженность должна быть меньше пробивной напряженности Ed. Из (5.8) после дифференцирования по r2 и приравнивания производной к нулю получим минимальную напряженность внутреннего провода при отношении радиусов
r2/r2=e. (5.71)

Рис. 5.44. Оптимизация с помощью смещения контурных точек
В этом случае оптимальная напряженность
![]() (5.72)
(5.72)
5.3.1.2. Сферический конденсатор.
Аналогичная оптимизация сферического конденсатора из уравнения (5.6) дает оптимальное отношение радиусов
![]() (5.73)
(5.73)
5.3.2. Численная оптимизация
К настоящему времени известны два способа численной оптимизации, пригодных для обычных форм электродов. Оба способа базируются на методе эквивалентных зарядов.
5.3.2.1. Смещение контурных точек.
Этот способ позволяет достичь требуемого распределения напряженности поля за счет итеративного смещения контурных точек. Для оптимизации распределения напряженности изменяется кривизна поверхности в соответствии с итеративным процессом отклонения напряженности до требуемого значения шаг за шагом [5.39].
Принцип такого метода оптимизации поясняется на рис. 5.44. Рассчитывается распределение напряженности электрического поля по некоторой подходящей исходной форме, в частности по поверхности, которая должна быть оптимизирована.
Для расчета напряженности поля используется метод эквивалентных зарядов, при этом рассчитываются коэффициенты матрицы, затем матрица обращается, и из физических краевых условий определяются эквивалентные заряды. После расчетов распределения напряженности проводится сравнение с желаемыми значениями напряженности и рассчитываются необходимые изменения формы с учетом связи изменений кривизны поверхности и напряженности.
Многократные «прогонки» по петле оптимизации, выделенной на рис. 5.44 жирной линией, дают требуемое изменение формы оптимизированного электрода.

Рис. 5.45. Оптимизация за счет изменения эквивалентных зарядов
5.3.2.2. Изменение системы эквивалентных зарядов.
Этот способ позволяет достичь оптимальной формы электродов путем изменения системы эквивалентных зарядов. Математически это означает решение задач электростатического поля наложением частных решений дифференциального уравнения Лапласа. Частные решения являются потенциальными функциями эквивалентных зарядов [5.6, 5.20]. При этом способе оптимизации электродная система делится на заданные участки, которые в процессе решения не меняются, и на переменные участки, подлежащие оптимизации. Не изменяющиеся участки отображаются, как это принято в методе эквивалентных зарядов, некоторым числом п контурных точек, которым соответствует-система эквивалентных зарядов Q в определенных местах, но пока с неизвестными значениями зарядов. Оптимизируемому участку электрода соответствуют п эквивалентных зарядов с заданными положениями и значениями зарядов. Заданные оптимизирующие заряды Q соответствуют заданным частным решениям математической задачи. Вследствие свойства линейной суперпозиции всех частных решений достаточно для выполнения граничных условий и определения недостающих частных решений из линейной системы уравнений (рис. 5.45).
Для отображения неоптимизируемых участков электрода краевым условием является потенциал соответствующих контурных точек. Для этого должны быть выбраны значения неизвестных эквивалентных зарядов так, чтобы они совместно с зарядами оптимизации создали требуемый потенциал Ф. Для каждой контурной точки должно выполняться условие
 (5.74)
(5.74)
Это уравнение означает, что при наложении все заряды оптимизации и эквивалентные заряды, умноженные на соответствующие потенциальные коэффициенты![]() , для k-й контурной точки дают потенциал Фk. Математически это записывается в виде
, для k-й контурной точки дают потенциал Фk. Математически это записывается в виде
![]() (5.75)
(5.75)
В (5.75) известно положение системы зарядов Qj, а для системы Qi известны положения и значения зарядов. Так как известны также места контурных точек и желаемый потенциал, то неизвестным оказывается лишь вектор эквивалентных зарядов Qj. Если все известные величины перенести в правую часть системы уравнений, то получим линейную систему уравнений
![]() (5.76)
(5.76)
В правой части уравнения учитывается влияние зарядов оптимизации на требуемый потенциал контурных точек.
В результате решения уравнения (5.76) определяются значения эквивалентных зарядов и затем рассчитывается эквипотенциальная поверхность, образуемая эквивалентными зарядами и зарядами оптимизации.
В оптимизируемой области на распределение напряженности на эквипотенциальной поверхности влияет изменение зарядов оптимизации Q, при этом изменяются их положения и значения. Оптимизация напряженности на поверхности электрода осуществляется в ходе итеративного процесса при смещении зарядов или изменениях их значений до тех пор, пока не достигается требуемое для оптимального распределения на« пряженности изменение радиуса электрода.
Точность этого способа очень высока, так как исходной точкой является не форма электрода, которая может быть приближенно определена контурными точками и системой эквивалентных зарядов, а эквипотенциальные поверхности, которые точно задаются системой зарядов.
По сравнению с обычным расчетом поля в этом случае требуется меньшее количество первоначальных контурных точек и эквивалентных зарядов. Отсутствие контурных точек на участках оптимизации значительно снижает необходимый объем памяти машины при решении матрицы коэффициентов, так как число элементов матрицы пропорционально количеству контурных точек.
Требующие машинного времени операции (построение матриц и ее инверсия) проводятся только однократно в процессе решения.
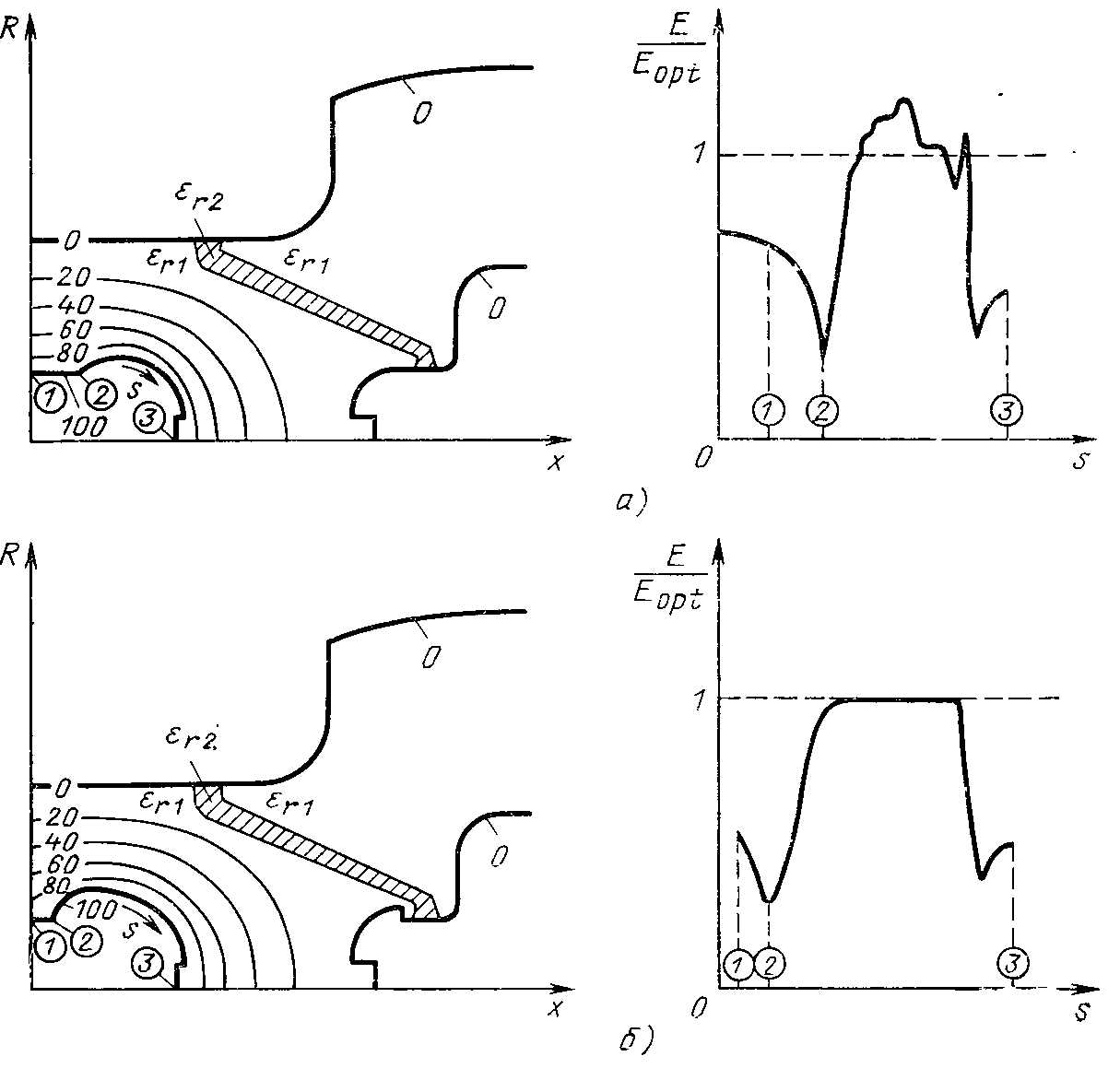
Рис. 5.46. Оптимизация электродов разъединителя:
а — картина поля и напряженность на поверхности электрода до оптимизации; б — то же после оптимизации; 1—3 — характерные точки поверхности электрода
На рис. 5.46 приведен пример оптимизации электродов разъединителя элегазового распредустройства. Устройство цилиндрически симметрично. На рис. 5.46,а изображены эквипотенциал при неоптимизированном электроде, а также изменение напряженности по длине электрода. После оптимизации у электрода напряженность постоянна (рис. 5.46,6). В этом случае оба главных электрода не сильно взаимосвязаны по полю, и поэтому они могут быть оптимизированы отдельно друг от друга.

