Сравнение численных способов расчетов поля
Сравнение численных способов расчетов поля может быть проведено с различных точек зрения.
Прежде всего представляет интерес точность расчетов напряженности поля на электродах. Имеют также значение адаптивность способа при конкретных обстоятельствах и требуемые для расчетов машинное время и объем памяти ЭВМ [5.18].
Принципиальные причины погрешностей численных способов.
Оба численных метода, в основе которых лежит рассмотрение проблемы в дифференциальной форме (дифференциальный способ и способ конечных элементов), требуют разбиения пространства на участки. Это разбиение с учетом объема памяти не может быть осуществлено на сколь угодно малые элементы, что обусловливает появление погрешности дискретизации. Другой источник принципиальных погрешностей связан с формой элемента сетки. Если закругленные участки электродов имитируются элементами с линейными сторонами, то в местах изломов получается наибольшая напряженность поля.
В способе конечных элементов при экстраполяции потенциала линейным полиномом появляется зависимость разницы напряженностей поля в местах изгибов от угла изгиба β (рис. 5.42).
Эту погрешность можно существенно уменьшить за счет использования полиномов более высоких порядков или элементов с плавными границами.
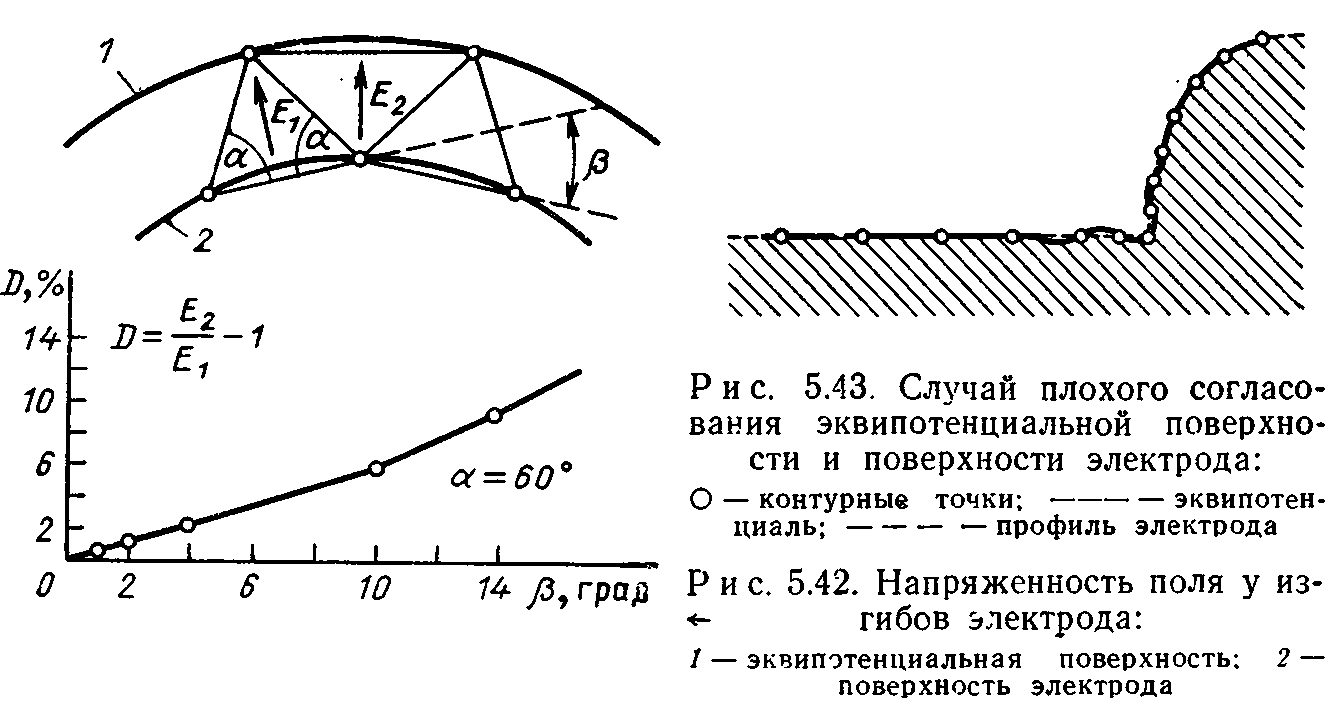
Остановимся на дальнейших принципиальных источниках погрешностей. Принимаемый закон изменения потенциала описывает действительное его изменение лишь приближенно. Поэтому возникает погрешность уже при самом введении закона изменения потенциала.
Следующая погрешность возникает из-за того, что минимизации энергии поля по принятой и действительной функциям расходятся. Из-за этого условия электростатического поля, которые получены не непосредственно из системы уравнений, выполняются лишь приближенно.
Способ эквивалентных зарядов использует интегральный подход при решении полевых задач, при этом части электрода заменяются конечным числом контурных точек. Качество замены зависит от того, как точно согласованы эквипотенциальная поверхность, образованная системой зарядов, с поверхностью электрода. Рассчитанная напряженность в контурных точках в точности соответствует напряженности на эквивалентной поверхности и приближенно напряженности на поверхности электрода.
Поэтому свойства способа во многом зависят от положения зарядов, использованных для имитации электрода, при этом важную роль играет расстояние между контурными точками и зарядами, а также их расположение. При неудачном расположении между контурными точками образуются волнообразные эквипотенциальные поверхности, искажающие напряженность на поверхности электродов. В частности, имитировать углы на поверхности электродов удается только с определенными ограничениями (рис. 5.43).
Напряженность поля на вершине волнообразной эквипотенциали выше, а на впадине ниже, чем на поверхности реального электрода. Кроме того, возникает погрешность в углах.
При расчетах методом Монте-Карло возникает погрешность совсем другого рода, связанная со статистическим разбросом среднего значения потенциала.
Преимуществом этого метода является то, что можно проанализировать среднее значение с учетом легко рассчитываемого разброса и при необходимости можно увеличить число случайных обходов.
Адаптивность, объем памяти и машинное время.
Численные способы позволяют универсально использовать их для расчетов сложных трехмерных полей, включая поля с различными диэлектриками. В то время как способом эквивалентных зарядов можно рассчитать одноэлектродные и многоэлектродные устройства, методы конечных элементов и дифференциальный метод требуют знания потенциалов на границе обоих электродов. Можно, однако, этими методами рассчитывать и одноэлектродные устройства, если элементы сетки распространить далеко от электрода, чтобы краевой эффект стал пренебрежимо малым.
Системы линейных уравнений, которые должны решаться при обоих способах, сильно различаются между собой. При дифференциальном методе и методе конечных элементов получаются относительно большие матрицы, характеризующие потенциальные условия всего поля. Однако они могут быть слабо заполнены. При методе эквивалентных зарядов для решения уравнения используют только краевые условия на электродах. Пространство, занятое полем, не входит в решение. Поэтому матрица становится меньшей размерности, однако в ней заполнены все места.
Поэтому для решения систем уравнений используются раз* ные методы. Расчет с помощью эквивалентных зарядов выполняется несколько быстрее и требует меньшего объема памяти ЭВМ. Однако в результате расчета получается решение только в виде системы зарядов. Потенциал и напряженность поля в каждой точке требуется рассчитывать как наложение вкладов всех зарядов.
При способах конечных элементов и дифференциальном способе получается решение в виде потенциала всех точек сетки.
Если поверхности электродов закруглены, больше подходит способ эквивалентных зарядов. Для расчетов систем с кромками и углами лучше использовать метод конечных элементов. Расчет систем, содержащих разные диэлектрики, упрощается при разбиении изоляции на элементы. В этом случае для учета границ раздела необходимо знать только разницу диэлектрических проницаемостей. При использовании метода эквивалентных зарядов, напротив, необходимо принять либо две системы точечных зарядов, либо поверхностный заряд на границе раздела; оба случая требуют больших затрат времени, однако граничные условия при этом удается соблюсти лучше.
Точность способов разбиений пространства на элементы может быть повышена в результате дальнейшего дробления элементов, а также за счет введения полиномов более высоких порядков. Единственным ограничением при этом является объем памяти машины. Улучшение результатов расчетов способом эквивалентных зарядов достигается не только одним повышением числа зарядов, но прежде всего координацией всей системы зарядов [5.11].
Для применения метода Монте-Карло существенно то, что следует задаться только конфигурацией электродов, которую можно взять по каталогу форм основных тел. Потребность в необходимом машинном времени относительно велика, так как для каждой обсчитываемой точки требуется большое число (например, 2000) случайных путей обхода и необходимо производить расчет для каждого случайного шага на минимальном расстоянии от электрода или границы сред.
Однако этот метод ограничивается меньшими критическими областями поля и может быть использован прежде всего для расчетов трехмерных полей.

