Эксплуатационные режимы электроэнергетических систем - Возникновение высших гармонических

РАЗДЕЛ ШЕСТОЙ
МАГНИТНОЕ НАСЫЩЕНИЕ В НЕПОДВИЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
ГЛАВА ДВАДЦАТЬ ТРЕТЬЯ
ВОЗНИКНОВЕНИЕ ВЫСШИХ ГАРМОНИЧЕСКИХ
Для того чтобы электрические установки и системы могли эффективно работать, необходимо, чтобы изменение тока и напряжения во времени происходило по возможности без каких- либо отклонений от наиболее благоприятного режима. В установках и сетях постоянного тока желательно, чтобы ток и напряжение были неизменны, так как при колебаниях напряжения лампочки мигают, а двигатели работают лишь со средней нагрузкой, и, кроме того, меняют свою частоту вращения. В системах переменного тока изменение напряжения и тока должно быть синусоидальным, поскольку основные потребители трехфазного тока — асинхронные двигатели — для создания своих рабочих вращающихся полей нуждаются в чисто синусоидальных напряжениях и токах. Любое отклонение от синусоидальной формы приводит к появлению в двигателях паразитных полей, не только бесполезно расходующих энергию, но и снижающих полезный вращающий момент двигателя.
Наконец, любое отклонение от желательного характера изменения постоянного или переменного тока, сопровождаемое образованием напряжений и токов более высокой частоты, приводит к многочисленным нарушениям нормальных режимов работы как в самой электрической сети, так и вне ее. Они могут создавать значительные перенапряжения и сверхтоки с их опасными воздействиями в виде пробоев и перегораний, а также приводить к появлению шума и качания машин, искрению щеток на коллекторах и сильному влиянию на соседние линии, особенно линии связи.
Отклонения постоянного тока и напряжения от заданного характера изменения, а переменного тока и напряжения от синусоидального изменения проявляются в виде высших гармонических. На рис. 1 кроме постоянной величины, а на рис. 2 кроме основного колебания показаны типичные высшие гармонические ип для обоих видов напряжения — постоянного и переменного. Причины их появления кроются в конструкции и принципе действия вращающихся электрических машин, трансформаторов, выпрямителей, аппаратов и линий передачи.
Периодические колебания, форма кривых которых точно повторяется через определенное время, можно на основании теоремы Фурье представить в виде суммы синусоидальных и косинусоидальных колебаний, частоты которых кратны основной частоте. Следовательно, периодическую функцию f(ωt) с основной круговой частотой ω можно разложить в ряд

Слагаемое A0 появляется только в тех случаях, когда кривая имеет апериодическую составляющую; An и Вп представляют собой амплитуды колебаний η-го порядка, а то — круговую частоту п-го составляющего колебания. Если кривые имеют более или менее плавные переходы, то амплитуды составляющих колебаний быстро убывают с повышением их порядкового числа п, так как существенное значение имеют только составляющие колебания низших порядков. Зубчатые кривые содержат также и более высокие гармонические с заметными амплитудными значениями.
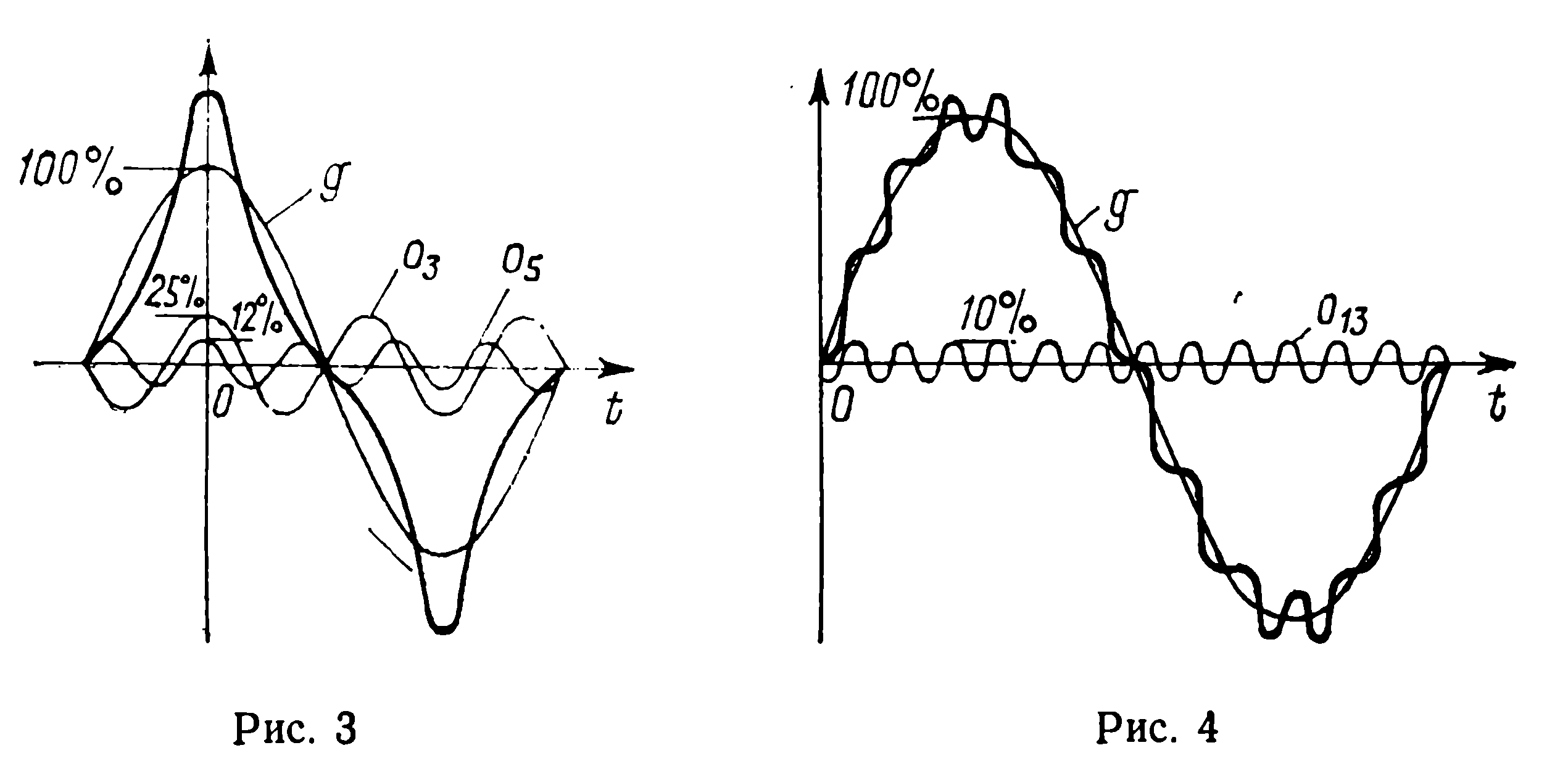
На рис. 3 приведена кривая, которая содержит одну 3-ю гармоническую с амплитудой 25% и одну 5-ю гармоническую с амплитудой 12% амплитуды основного колебания. На рис. 4 построена кривая, содержащая только 13-ю гармоническую с амплитудой, равной 10% среднего значения основного колебания. Если положительная и отрицательная полуволны кривой имеют одинаковую форму, то все четные гармонические отсутствуют. В случае четной функции, когда кривая симметрична относительно оси ординат, как это представлено на рис. 3, ее разложение состоит только из косинусоидальных членов, а в случае нечетной функции, как на рис. 4, при разложении получаются только синусоидальные члены.
Разложение заданной кривой в гармонический ряд по уравнению (1) является произвольным. В некоторых случаях можно было бы с успехом применить разложение по другим функциям.

Однако метод гармонического анализа дает особые преимущества при рассмотрении различных колебательных процессов, так как решение линейных дифференциальных уравнений, описывающих эти колебания, наиболее удобно выражаются через гармонические функции. Поскольку такие уравнения встречаются в задачах, связанных со многими проблемами электротехники, то метод гармонического анализа находит широкое практическое применение. Нельзя, однако, упускать из вида, что при исследовании многих явлений разложение на гармонические составляющие не способствует более глубокому проникновению в физику процесса, в частности когда необходимо рассматривать характер кривых в целом либо их отдельных участков.