Проблема сравнения эффективности вычислительных процедур, соответствующих различным методам оптимального проектирования, не является простой. Дело в том, что для сравнения эффективности необходимо задаться некоторым критерием, в качестве которого может быть выбрана точность получаемого результата, время счета, объем необходимой памяти вычислительной машины .и т. д. Однако даже конкретизация критерия эффективности не позволяет однозначно упорядочить все алгоритмы и сказать, какой из них лучше, а какой хуже. Это объясняется тем, что оценки алгоритмов выполняются не для одной задачи, а для классов задач. Поэтому плохой для широкого класса задач алгоритм может оказаться эффективным на более узком классе. Исходя из этого, ограничим подкласс рассматриваемых задач задачами оптимального проектирования силовых трансформаторов и сопоставим используемые при этом алгоритмы.
При оценке того или иного вычислительного алгоритма необходимо рассмотреть следующие его характеристики [75]:
- Полнота. Под этой характеристикой понимается, достаточно ли четко сформулированы правила, описывающие рассматриваемый алгоритм, чтобы человек или ЭВМ могли следовать им, обладая лишь умением считывать информацию и не прибегая ни к каким дополнительным рассуждениям и умозаключениям.
- Свойства сходимости. Всегда ли вычислительная процедура, определяемая данным алгоритмом, обеспечивает сходимость? Если сходимость имеет место, всегда ли она приводит к правильному решению? Сколько итераций необходимо выполнить при решении той или иной практической задачи, чтобы получить требуемый результат?
- Требования к вычислительным процедурам. Насколько сложными и трудоемкими оказываются вычисления, которые необходимо выполнить для получения надлежащего решения? Каково полное время вычислений?
- Область применения. Для решения каких математических задач предназначен данный алгоритм? Насколько легко определить, попадает ли рассматриваемая конкретная задача в класс, покрываемый областью применимости алгоритма?
Так как проблема сходимости при использовании различных алгоритмов является наиболее сложной, в целях иллюстрации поясним ее на примере простои модели. Пусть требуется максимизировать некоторую целевую функцию. На рис. 4.20 показано, как изменяется значение целевой функции при переходе от одной итерации к следующей для различных алгоритмов:
а) Улучшение значения целевой функции наблюдается при каждой итерации. Ряд пробных значений сходится к оптимальному решению после выполнения конечного числа итераций.
б) Улучшение значения целевой функции наблюдается при каждой итерации, однако итерационный процесс содержит бесконечное число итераций. Оптимальное решение достигается в данном случае лишь асимптотически.
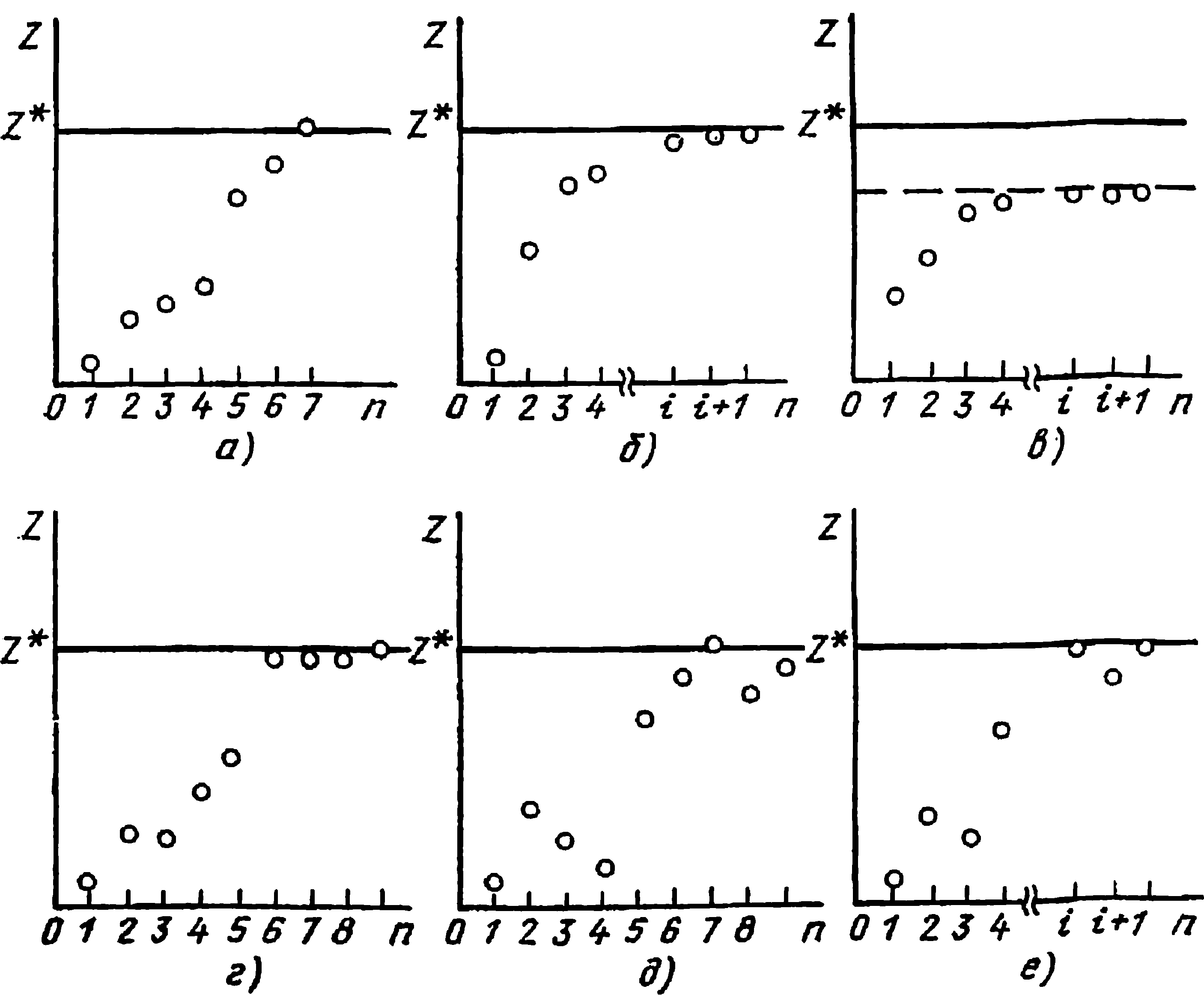
Рис. 4.20. Иллюстрация сходимости
в) Как и в предыдущем случае, итерационный процесс содержит бесконечное число итераций. Однако целевая функция стремится к некоторому значению, лежащему ниже оптимального.
г) Ряд значений сходится к оптимальному за конечное число итераций, причем при каждой последующей итерации, по крайней мере, не происходит ухудшения предыдущего результата.
д) Стабильной сходимости сопутствует наблюдающееся при некоторых итерациях убывание значения целевой функции.
е) Асимптотическому достижению оптимального результата сопутствуют временные убывания целевой функции при некоторых итерациях.
Таким образом, не любой алгоритм обеспечивает сходимость пробных значений целевой функции к некоторому предельному, значению за конечное число итераций. В тех случаях, когда сходимость имеет место, предел, к которому стремится целевая функция, не всегда совпадает с ее оптимальным значением. Скорость сходимости является одним из двух факторов, влияющих на полное время вычислений, другим (если не учитывать характеристик ЭВМ, на которой производятся расчеты) является время, затрачиваемое на одну итерацию.
Подводя итог вышесказанному, отметим, что выбор алгоритма при оптимизации конкретной задачи должен производиться исходя из минимального значения функции [67]
![]() (4.52)
(4.52)
где Φι — затраты на вычисления, связанные с оптимизацией функции Z(X); Ф2(b) —потери, возникающие в связи с тем, что некоторый метод b не гарантирует нахождение абсолютного экстремума функции Z(X).
В двух предыдущих параграфах указывалось, что и рационализированный перебор (РП), и случайный поиск (СП) являются эффективными алгоритмами промышленного проектирования силовых трансформаторов средней мощности. С расширением класса решаемых задач каждый алгоритм имеет свой предел применимости, что делает необходимым определить области их наиболее эффективного использования применительно к вычислительным машинам одной производительности. В настоящем параграфе выполнено сравнение этих алгоритмов на основе сопоставления результатов проектирования серии трансформаторов 35 кВ с оптимизацией по различным критериям, а также опыта эксплуатации алгоритмов РП и СП.
Исследования показывают, что оба алгоритма с точки зрения полноты описания и однозначности правил последовательной реализации на ЭВМ являются совершенно равноценными. Об этом свидетельствует отсутствие отклонений от нормальной работы (зацикливаний, аварийных остановов и т. д.) при задании исходных данных в установленных пределах, а также полный учет всех требований к проектируемому объекту, т. е. трансформатору. Первая точка пробного решения, позволяющая начать реализацию алгоритма, в каждом случае находится автоматически. Последующие сочетания регулируемых параметров при случайном поиске определяются по формулам (4.47) и (4.48), а в методе перебора по выражению вида
(4.53)
![]()
где mi — число разбиений исходного интервала Li, определяемого предельными значениями хib и Xiн. Критерием останова в первом случае является выполнение условия (4.51), а во втором — перебор всех значений, принадлежащих допустимой области.
Что касается сходимости, то вычислительные процедуры алгоритмов РП и СП всегда обеспечивают сходимость оптимизационного процесса при широких допустимых вариациях исходных данных, о чем свидетельствуют обязательная выдача результата и предусмотренный программой останов ЭВМ. Что касается сходимости к правильному решению (глобальному экстремуму), то для метода перебора однозначному ответу на этот вопрос препятствует дискретный характер регулируемых параметров, а именно: для сокращения времени расчета перебор некоторых регулируемых параметров (например, W1) ведется не с единичным шагом (1 виток), а с некоторым значением ki≠1 (4.53). Поэтому действительный экстремум может находиться от найденного на расстоянии ki<2, что обусловливает некоторую ошибку его определения. В методе СП подобная ситуация, учитывая пологий характер целевой функции в области оптимума, также не исключается. Более того, здесь, имеет место ненулевая вероятность застревания системы в одном из локальных экстремумов. Однако подобные возможности реализуются с низкой вероятностью. Используя рис. 4.20 для иллюстрации сказанного, можно констатировать, что для РП наиболее типична ситуация, показанная на рис. 4.20,д, а случайный поиск сходится к решению согласно всем остальным схемам. В табл. 4.6 приведены результаты проектирования трансформаторов серии ТМ двумя различными методами с оптимизацией по минимуму народнохозяйственных затрат.
Следует отметить, что вероятность нахождения одного и того же варианта при оптимизации трансформатора различными алгоритмами является крайне низкой, что объясняется пологим видом целевой функции вблизи экстремума. Так, как правило, значение критерия эффективности у десятого варианта отличается от наилучшего в среднем не более чем на 0,15%, а полное количество вариантов, имеющих значение целевой функции в пределах Zmin+ΔΖ (где ΔΖ равно 0,5% Zmin), составляет от 102 до 7-102 вариантов в зависимости от вида критерия эффективности.
Различные наборы варьируемых параметров и большое многообразие подвергаемых анализу вариантов резко снижают вероятность дублирования оптимального результата при использовании разных алгоритмов. Тем не менее из табл. 4.6 видно, что оптимизация по народнохозяйственным затратам приводит к расхождениям окончательных результатов, не превышающим 0,5%.
Таблица 4.6. Результаты проектирования серии трансформаторов методами минимуму народнохозяйственных затрат
Мощность трансформатора. кв· А | Алгоритм | Народно-хозяйственные | Масса | Масса | Потери КЗ, Ет | Потерн XX, Вт |
1000 | РП | 4658,4 | 398,3 | 1426,0 | 10 578 | 2526 |
| СП | 4639,0 | 358,1 | 1380,1 | 11826 | 2457 |
1600 | РП | 6289,9 | 551,6 | 1912,7 | 15 903 | 3079 |
| СП | 6300,0 | 548,6 | 1886,2 | 15 424 | 3320. |
2500 | РП | 8554,2 | 627,6 | 2664,8 | 22 125 | 4534 |
| СП | 8595,1 | 700,2 | 2655,8 | 20500 | 4836 |
4000 | РП | 11833,0 | 891,9 | 3715,7 | 30724 | 6209 |
| СП | 11891,9 | 871,4 | 3694,9 | 31269 | 6403 |
6300 | РП | 16241,1 | 1257,5 | 4830,8 | 46120 | 8024 |
| СП | 16287,4 | 1154,7 | 4652,5 | 47292 | 87.24 |
Как правило, незначительно различаются значения варьируемых параметров, соответствующие оптимальным вариантам, что свидетельствует о сходимости вычислительных процессов к истинному экстремуму. Более заметные расхождения оптимальных значений варьируемых параметров свидетельствуют о том, что найденные точки не локализованы в окрестности глобального экстремума, а расположены в разных частях допустимой области. Тот факт, что в этих точках целевая функция имеет почти одинаковые значения, подтверждает правильность вывода о сложной конфигурации допустимой области и существовании большого количества локальных экстремумов, среди которых возможны приблизительно равноценные. Из табл. 4.6 видно, что случайный поиск лишь в одном случае приводит к лучшему результату. При данном критерии эффективности это соотношение является типичным.
Оптимизация по стоимости трансформатора дает иную картину. Расхождение между конечными результатами оказывается меньшим, а случайный поиск в четырех случаях из пяти дает лучший результат. Это объясняется следующим: оптимизация проводилась на серии трансформаторов с линейным напряжением обмотки НН, равным 10,5 кВ, что определило шаг по числу витков обмотки НН в алгоритме РП ΔW1=5-10 витков. Следовательно, для алгоритма на основе РП можно говорить об определении экстремума с точностью ΔW1/2, заложенной в исходных данных. Случайный поиск подобной, неизбежной для рационализированного перебора, ошибки не имеет. Однако при оптимизации по народнохозяйственным затратам, когда общее число вариантов примерно на 25—30% превышает их количество при оптимизации по стоимости трансформатора, случайный поиск дает несколько меньшую эффективность. Это вызвано, очевидно, увеличением количества примерно равноценных вариантов и усложнением ситуации конечного выбора на завершающем этапе.
Таким образом, при оптимизации по стоимости трансформатора, а также в любом другом случае с достаточно выраженным глобальным экстремумом случайный поиск по точности сходимости рационализированного перебора и случайного поиска с оптимизацией по не уступает методу рационализированного перебора.
| Напряжение КЗ, % | Индукция в стержне, Тл | Диаметр стержня магнитопровода, см | Высота окна, см | Межосевое | Плотность тока в обмотках, А/mm2 |
| 6,29 | 1,579 | 22 | 107,0 | 50,0 | 1,45; 1,77 |
| 6,79 | 1,567 | 22 | 101,5 | 49,5 | 1,57; 2,06 |
| 6,41 | 1,535 | 24 | 127,5 | 51,5 | 1,47; 1,83 |
| 6,76 | 1,571 | 24 | 123,5 | 52,5 | 1.50; 1,69 |
| 6,35 | 1,562 | 28 | 121,5 | 56,5 | 1,61; 1,96 |
| 6,78 | 1,585 | 28 | 118,5 | 58,5 | 1,37; 1,95 |
| 7,30 | 1,546 | 32 | 121,5 | 64,0 | 1,54; 1,86 |
| 7,28 | 1,545 | 32 | 124,5 | 63,5 | 1,63; 1,86 |
| 7,45 | 1,552 | 34 | 153,0 | 66,0 | 1,65; 1,83 |
| 7,42 | 1,607 | 34 | 141,5 | 66,5 | 1,65; 2,12 |
Появление большого количества равноценных вариантов (оптимизация по народнохозяйственным затратам) затрудняет достижение глобального экстремума, но даже в этом неблагоприятном случае отклонение от оптимума не превышает 0,5%.
Скорость сходимости итерационного процесса определяет общее время решения задачи. В алгоритме случайного поиска скорость сходимости оказывается выше, чем в алгоритме на основе РП (рис. 4.21). Причем в области экстремума сходимость случайного поиска заметно замедляется, причиной чего является пологий вид целевой функции. Эта особенность в характере изменения критерия эффективности не оказывает существенного влияния на сходимость в методе рационализированного перебора, для которого уменьшение целевой функции происходит сравнительно равномерно по ходу оптимизационного процесса и зависит в основном от степени влияния варьируемого на данном этапе параметра на оптимизируемый критерий.
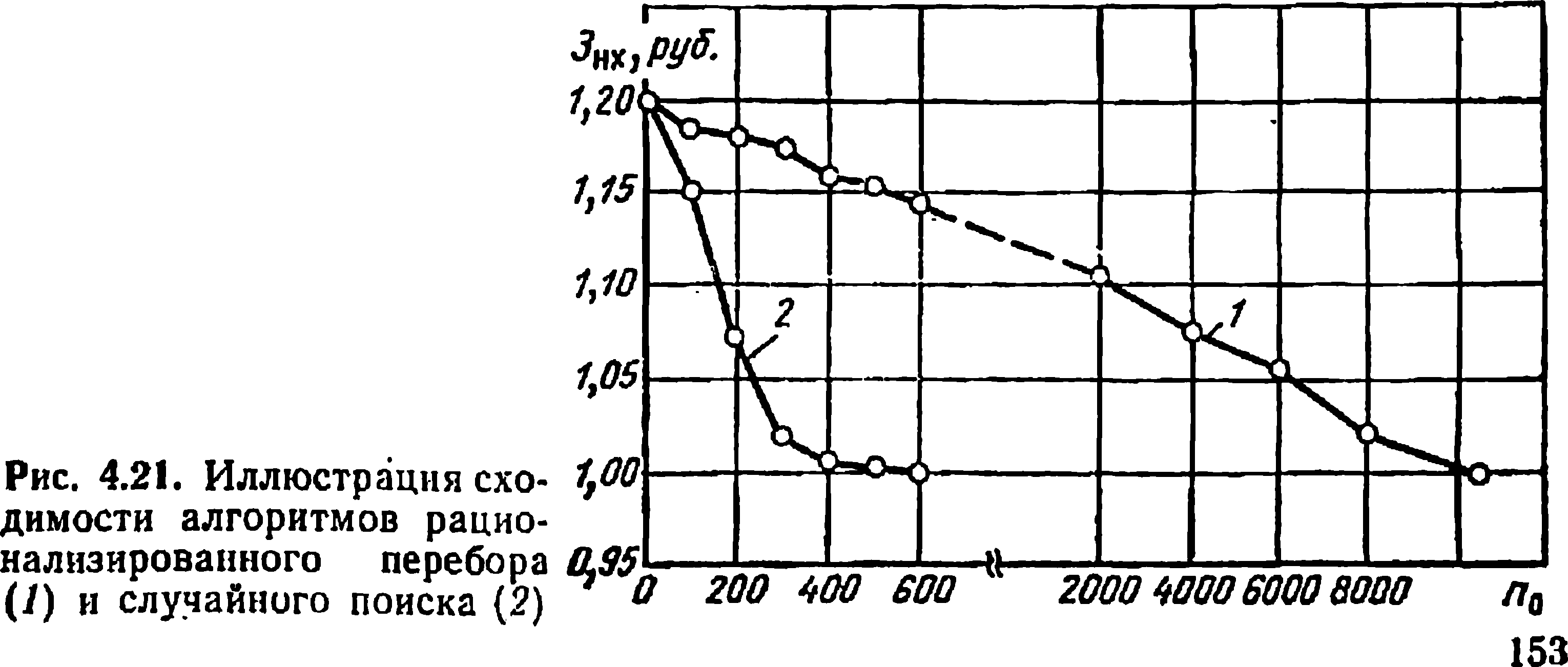

На рисунке показаны лишь сравниваемые вычислительные процессы с положительным результатом до момента достижения глобального экстремума. В табл. 4.7 приведены данные, характеризующие скорость сходимости при оптимизации трансформатора ТМ-1600/35 по минимуму народнохозяйственных затрат.
Из таблицы видно, что если в алгоритме СП осуществляется целенаправленное движение к экстремуму с небольшим числом обращений к модели после его достижения (не более 10—12 % от n0), то в РП количество вариантов, рассчитываемых после определения f*, достигает 40% и более. Чтобы показать, что отмеченный факт является не недостатком алгоритма, а свойством метода рационализированного перебора, зависящим от состава исходных данных, в табл. 4.8 приведены значения n0*, полученные при проектировании трансформатора ТМ-1600/35 при различных значениях диаметра стержня магнитопровода dp и напряжения КЗ.
Кроме скорости сходимости, на полное время расчета влияет время, затрачиваемое на одну итерацию. Для случайного поиска оно почти в 3 раза превышает время расчета одного варианта методом РП, что объясняется необходимостью многократного обращения к датчику случайных чисел (в среднем 10,2 раза для получения очередного Xk, принадлежащего допустимой области).
В табл. 4,9 приведены основные характеристики алгоритмов рационализированного перебора и случайного поиска, которые позволяют определить наиболее рациональные и эффективные области их применения.
Таблица 4.8


Метод РП при проектировании трансформаторов наиболее эффективен, когда число варьируемых параметров не превышает 4—5. Дальнейшее увеличение числа варьируемых параметров приводит к значительному возрастанию времени расчета (рис. 4.22). Случайный поиск менее чувствителен к размерности задачи. Возможность его применения определяется в первую очередь значением вероятности вхождения в допустимую область. При низких значениях p(D) нарушается динамичность метода и теряется его эффективность. Кроме того, при сложной конфигурации допустимой области и большом количестве резко выраженных локальных экстремумов снижается вероятность достижения глобального оптимума. В этом случае целесообразен многократный поиск из различных начальных точек.
При оптимизационном проектировании трансформаторов средней мощности оба разработанных алгоритма показали высокую надежность и эффективность. Почти полное совпадение результатов проектирования подтверждает правильное функционирование РП и СП, а также безусловную возможность нахождения глобального экстремума оптимизируемой функции.
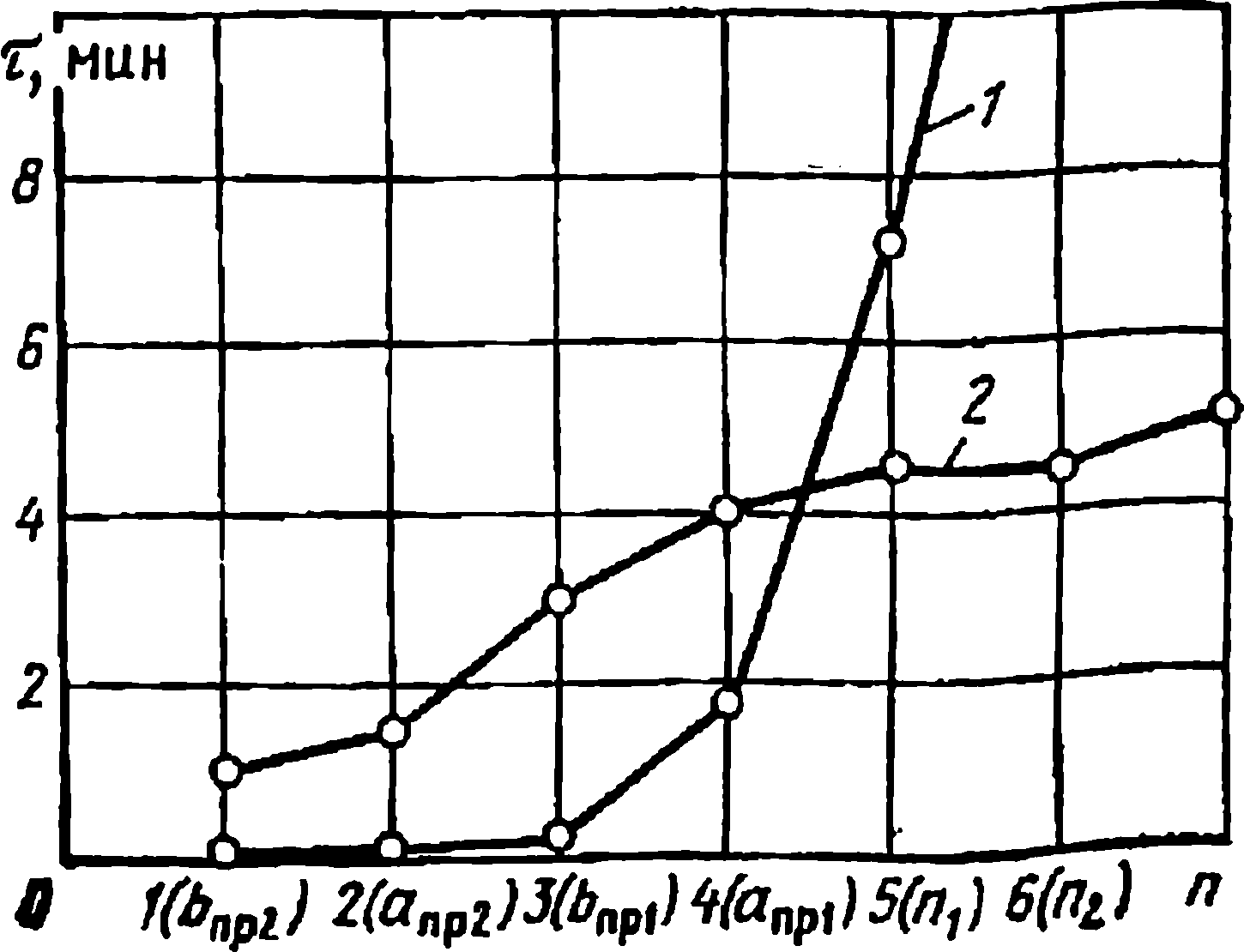
Рис. 4.22. Изменение времени расчета с ростом числа регулируемых параметров:
Относительно выбора метода для решения конкретной задачи можно отметить, что здесь критерием может служить формула (4.52).
В той случае, если предполагается промышленный выпуск проектируемого изделия, целесообразно для поиска оптимального варианта использовать РП. В случае единичных, предварительных и исследовательских расчетов метод случайного поиска чрезвычайно эффективен и незаменим. Определенные перспективы имеет сочетание разработанных алгоритмов с другими методами оптимизационного проектирования, а также друг с другом.

