4.6. Разработка и исследование оптимизационного процесса проектирования трансформаторов на основе метода случайного поиска
Случайный поиск как метод решения экстремальных задач получил наиболее широкое применение для случаев, когда размерность оптимизируемого объекта велика, а его математическая модель имеет достаточно сложный вид при наличии ограничений на некоторые параметры. Примером таких задач прежде всего являются задачи оптимального проектирования и, в частности, задача оптимального проектирования силовых трансформаторов.
Возможность вероятностного самообучения является следующей особенностью методов случайного поиска. Это означает, что в процессе поиска запоминается удачное направление движения (в сторону убывания целевой функции) и ему оказывается вероятностное предпочтение. Такая стратегия поиска является наилучшей по сравнению с теми, когда связь между соседними шагами отсутствует (метод перебора), т. е. система полностью игнорирует предыдущий опыт или, наоборот, эта связь выражена очень сильно (градиентный метод) — система слепо верит предыдущему удачному результату и движется к цели в этом направлении.
Ценное качество методов случайного поиска, как понятно из вышесказанного, заключается в том, что они требуют от минимизируемой функции лишь ее существования в любой точке области поиска экстремума (что характерно также для метода перебора), в то время как подавляющее большинство других методов математического программирования предполагает гладкость и дифференцируемость целевой функции.
Преимущества случайного поиска особенно проявляются с ростом размерности задачи. Если в методе перебора, градиентном и в ряде других, число необходимых испытаний системы с ростом размерности растет как п, то в случайном поиске — пропорционально √n. Последние два свойства объясняют широкую универсальность методов случайного поиска.
Приведенные алгоритмы представлены в принципиально простой форме, из которой не следует возможность их применения для решения конкретной задачи. Ниже подробно излагаются вопросы применения алгоритма случайного поиска для проектирования силовых трансформаторов.
При использовании простейшего случайного поиска для нахождения экстремума целевой функции силового трансформатора при наличии заданных ограничений вероятность работы в допустимой области РФ), как показали специальные исследования, не превышает 0,001. Вероятность обнаружения глобального экстремума при организации поиска только в допустимой области находится на уровне 0,0001. Таким образом, при коэффициенте доверия р=0,95-0,99 для решения задачи оптимизации необходимо выполнить около 107 испытаний, что свидетельствует о неприемлемости простейшего подхода для решения данной задачи.
В связи с этим основными проблемами при разработке алгоритма на основе случайного поиска при проектировании трансформатора являются:
- Повышение вероятности работы в допустимой области, в противном случае резко возрастает время поиска, нарушается динамичность метода, возникает опасность зацикливания расчета.
- Обеспечение нахождения глобального экстремума с наиболее высокой вероятностью.
- Выработка критерия останова системы.
В качестве варьируемых параметров примем первый дискретный набор переменных, приведенный в § 4.2. Каждый такой параметр, обозначаемый в дальнейшем через ξ, может принимать отдельные изолированные значения из соответствующего интервала L, которому поставлен в соответствие определенный закон распределения вероятностей. Принятие величиной ξ конкретного значения Xi оказывается случайным событием, а это означает, что:
это событие не произвольно, а подчинено некоторым закономерностям;
его можно в принципе повторять неограниченное число раз;
оно имеет определенную вероятность появиться при каждом испытании в заданных условиях.
Обратимся к произвольному набору случайных величин, обозначаемому в дальнейшем для краткости через ω' образуют множество А. Выделим совокупность исходов, которые приводят к попаданию случайной точки в допустимую область D. Вероятность этого события оценивается формулой
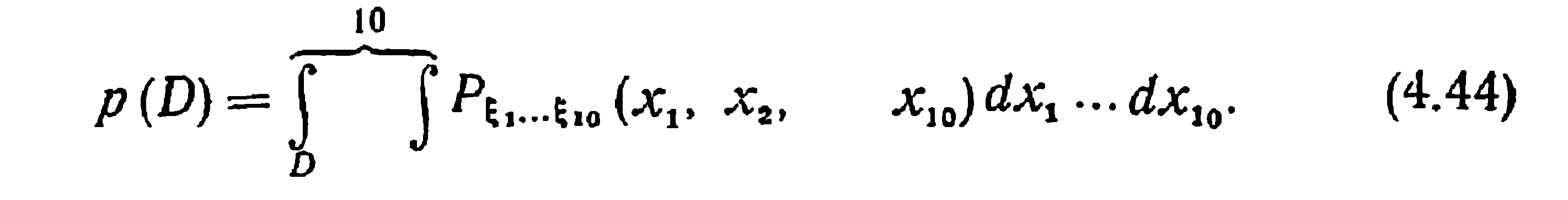
Аналитическое решение (4.44) представляется затруднительным, однако по опытным данным, как отмечалось выше, вероятность p(D) оказывается весьма низкой. Так как в геометрической интерпретации величина p(D) представляет отношение 10-мерных объемов областей D и А, то для ее повышения необходимо либо расширить допустимую область D, либо сузить пространство элементарных событий А.
В связи с тем, что первый путь практически невозможен, целесообразно уменьшить область А, рассматриваемую здесь как пространство элементарных событий. Это возможно сделать, во-первых, за счет отказа от случайной вариации dc ввиду того, что, как правило, задача решается не более чем для трех значений диаметра стержня магнитопровода. Во-вторых, случайный поиск некоторых параметров целесообразно заменить зависимым нахождением их из уравнений, определяющих границы допустимой области, как функции от остальных параметров, изменяющихся случайно. Это приведет к автоматическому удовлетворению ряда ограничений и повышению вероятности р (D).
Рассмотрим два уравнения, связывающих параметры трансформатора:

(4.45;
Первое уравнение устанавливает связь номинальных параметров трансформатора и геометрических размеров обмоток со значением реактивной составляющей напряжения КЗ. Второе — выражает условие равенства высот обмоток без зон регулировочной и разгона в двухобмоточном трансформаторе.
После ряда элементарных преобразований (4.45) относительно Z1 получаем уравнение вида
![]() (4.46)
(4.46)
Аналитические выражения для определения A1, А2, A3 и A4 приведены в [73]. Количество катушек обмотки ВН связано с Z1 выражением вида![]()
Уравнение (4.46) решается численным методом деления отрезка пополам с заданной точностью. В качестве исходного интервала принят расширенный диапазон возможного изменения числа катушек обмотки НН z1, равный 10—100. Специальные исследования, проведенные при широкой вариации исходных параметров [решение уравнения (4.46) методом Мюллера], показали, что на заданном интервале всегда существует единственный корень. Рассчитанные значения z1 и z2 округляются до меньших четных значений. После чего с установленным шагом (∆z=2-4) рассматриваются все сочетания zx и z2, удовлетворяющие следующим требованиям:
заданному значению напряжения КЗ;
недоходу витков в катушке обмотки НН;
недоходу витков в катушке обмотки ВН;
соотношению увеличенных и нормальных каналов в обеих обмотках.
Увеличение числа катушек возможно до тех пор, пока ик не выйдет из своего нижнего допуска. Таким образом, автоматическое удовлетворение ряда ограничений, имеющих наименьшие вероятности выполнения, за счет уменьшения числа регулируемых параметров и детерминированное определение dc позволяет повысить вероятность n(D) до 0,1+0,2.

В табл. 4.3 дано описание параметров, диапазоны их изменения соответствуют данным, приведенным в табл. 4.1.
Будем в дальнейшем очередной набор случайно изменяющихся параметров ξ1, ξ2,...., ξ7 обозначать через ω.

Рис. 4.12. Определение вероятности выбора размера провода с индексом 7. (Кривая нормального распределения вероятностей имеет следующие параметры:
Mj=11, 16)
Значения ξ3, ξ4, ξ5 вычисляются аналогично (4.48) и (4.49). Коэффициенты распределения вероятности предназначены для выравнивания плотности вероятности на всем исходном интервале изменения регулируемых параметров Li: k1=0,5-l,5 в зависимости от значения фазного напряжения обмотки НН; k2=k3=k4=k5= 4-5.
Событие Xi/Li является достоверным, так как возможный выход случайной величины за пределы интервала в формулах (4.47) и (4.49) исключается специальными проверками. На рис. 4.12 отношение площади заштрихованной фигуры ко всей площади под кривой pj представляет вероятность выбора из массива R размера провода с индексом 7. Для числа параллелей обмоток НН и ВН в зависимости от фазного тока определяются некоторые базовые значения количества параллелей и п2, относительно которых ведется выбор текущих значений ξ6 и ξ7 в соответствий с табл. 4.4 (для обмотки ВН аналогично).

Таблица 4.4
Иначе говоря, в начале расчета
![]()
(4.50)
В ходе расчета происходит перераспределение вероятностей выбора конкретных значений в пользу значения, соответствующего текущему экстремуму. Для реализации (4.50) используется случайная величина ξρ, равномерно распределенная в интервале.
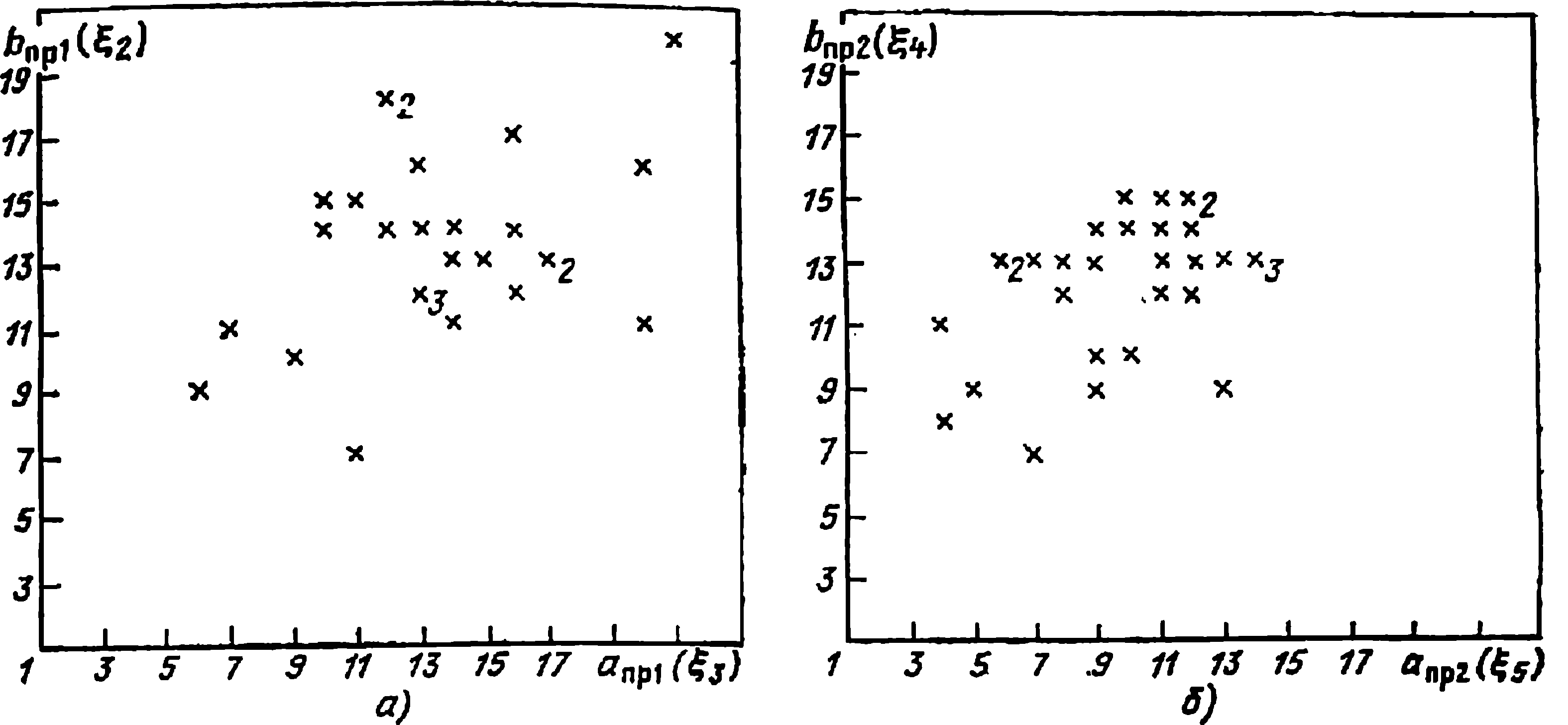
Рис. 4.13. Распределение 30 начальных точек при случайном поиске оптимального варианта трансформатора:
а —размеры провода обмотки НИ; б — размеры провода обмотки ВН
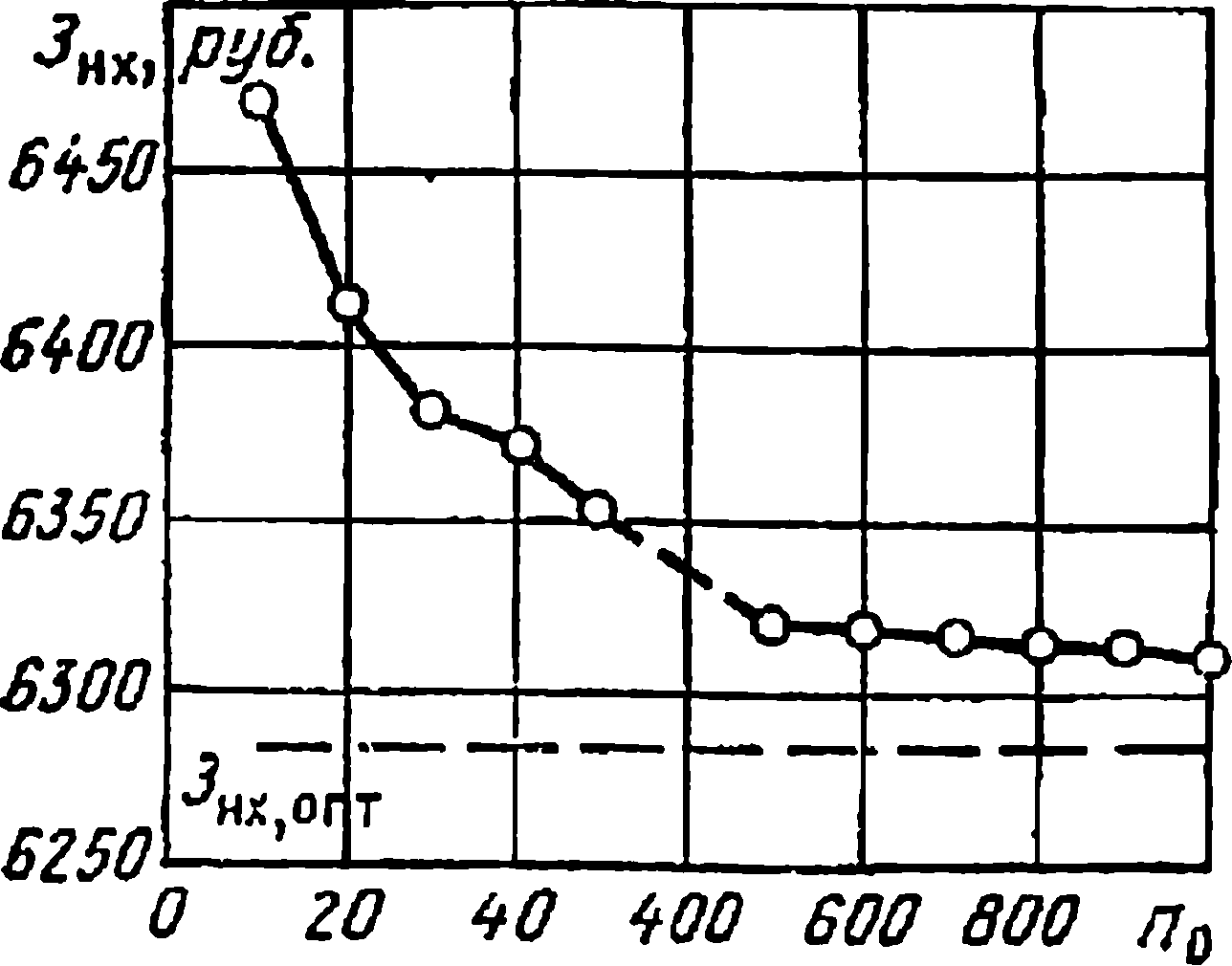
Рис. 4.14. Сходимость оптимизационного процесса в случае простейшего случайного поиска
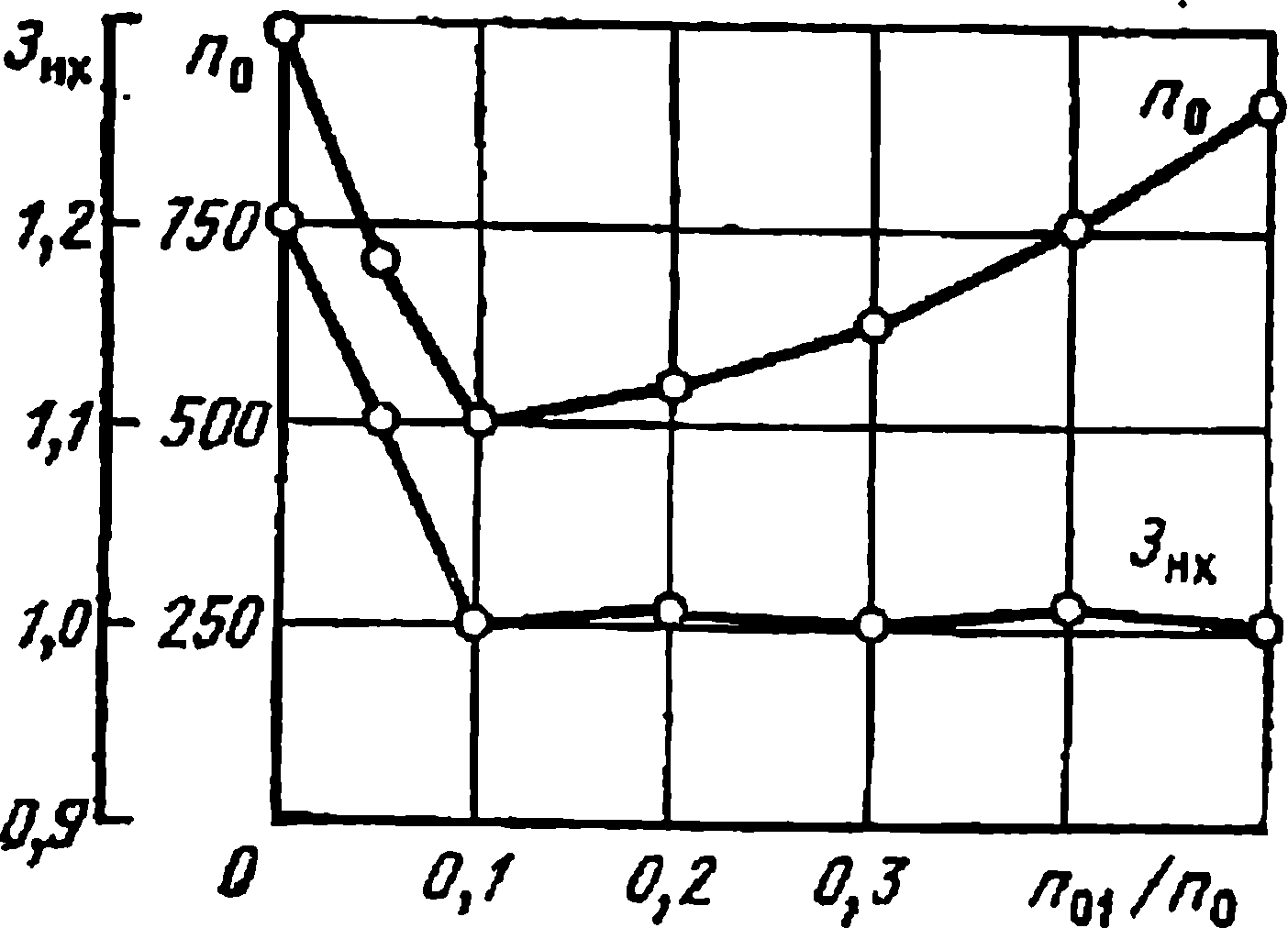
Рис. 4.15. Влияние на сходимость и продолжительность оптимизационного процесса п01/п0
Оптимизационный процесс поиска минимума целевой функции трансформатора разделяется на два этапа. Проведение равномерной выборочной оценки целевой функции по всей допустимой области D является основным назначением первого этапа. Начальные плотности вероятностей р случайных величин ξi задаются таким образом, чтобы разница между вероятностями выбора любых двух значений из соответствующего интервала Li равнялась нулю или была минимальной. Для этого нормальное распределение вероятностей задается с математическим ожиданием, соответствующим середине исходного интервала и дисперсией, максимальное значение которой определяется исходя из правила «трех сигм» (рис. 4.12). Таким образом, на первом этапе схема расчета эквивалентна простейшему случайному поиску, а вероятность достижения глобального экстремума в этом случае, как отмечалось выше, чрезвычайно низка. На рис. 4.13 показано расположение 30 начальных точек в двухмерных областях на первом этапе оптимизационного расчета трансформатора ТМ-1600/35. Кроме фактора случайности на заполнение областей вида Е2, ..., E7 первостепенное влияние оказывает характер допустимой области. Цифры на рисунке отмечают число случайных попаданий в одну и ту же точку.
Рис. 4.14 иллюстрирует сходимость оптимизационного процесса при изменении продолжительности начального этапа расчета. С увеличением числа обращений к математической модели, сходимость хотя и имеет место, однако при больших п0 темпы ее явно неудовлетворительны. Обработка многочисленных результатов расчетов трансформаторов с различным отношением продолжительности первого этапа ко всему времени расчета дает возможность построить зависимости, приведенные на рис. 4.15. Из рисунка следует, что существует некоторое оптимальное отношение, ниже которого не гарантируется стабильность сходимости, а при возрастании n01/n0 увеличивается время расчета. Значение (η01/η0)οпт приблизительно равно 1:10.
На втором этапе оптимизационного процесса обеспечивается тенденциозное движение к глобальному экстремуму, основанное на идее ползущего поиска [74]. Эта идея базируется на следующей теореме: если глобальный экстремум образует непустое подмножество С множества допустимых решений D, его окрестность с вероятностью, близкой к единице, содержит другие подмножества из этого множества.
Преемственность между двумя этапами оптимизационного процесса обеспечивается фиксацией координат точки ω*1-2, в которой целевая функция имеет наименьшее, определенное на первом этапе значение. Эти координаты используются в качестве исходных на втором этапе расчета, на котором за счет регулирования характеристик случайных величин происходит изменение стратегии поиска в направлении повышения вероятности выбора очередного значения ωк вблизи текущего экстремума при непрекращающемся поиске по всему пространству допустимой области. Изменение характеристик случайных величин производится по следующей схеме.
Математическое ожидание случайной величины Μξi соответствует точке текущего экстремума, так как мода нормального распределения вероятностей Рξi перемещается вслед за случайным движением χi* (рис. 4.16). Повышение вероятности поиска в окрестности текущего экстремума обеспечивает направление траектории поиска к глобальному минимуму целевой функции на основании вышеприведенной теоремы. Постоянные случайные испытания, проводимые по всему объему допустимой области, препятствуют нежелательному останову системы в одном из локальных экстремумов, обеспечивая ненулевую вероятность скачкообразного продвижения к глобальному минимуму оптимизируемой функции (рис. 4.17).

Рис. 4.16. Флуктуация математических ожиданий случайных величии на втором этапе оптимизационного процесса. (В скобках по оси абсцисс указано количество обращений к математической модели).
Математическое ожидание Mξi каждой из семи переменных изменяется независимо от вероятностных характеристик других случайных величин. Результат будет достигнут, когда искомые координаты точки ωn* совпадут с математическими ожиданиями соответствующих переменных.
При случайном поиске с постоянным шагом вероятность удачного шага уменьшается по мере приближения к цели. Например, при оптимизации двухпараметрической квадратичной целевой функции вероятность удачного шага определена следующим образом:
![]()
где а — рабочий шаг; R — радиус кривизны линии равного уровня целевой функции в точке выбора очередного шага.
Как видно из предыдущей формулы, при приближении к цели, чему соответствует уменьшение R, вероятность р' уменьшается от 0,5 при R→∞ до нуля при R=а/2. Ситуация не меняется с увеличением размерности задачи.

В рассматриваемом алгоритме случайного поиска регулирование среднего шага осуществляется за счет изменения дисперсии случайных величин.
На первом этапе расчета дисперсия Dξi, как отмечалось выше, .задается таким образом, чтобы обеспечить приблизительно равновероятную возможность выбора любых значений из соответствующего интервала Li. Управление поиском оптимума целевой функции за счет регулирования дисперсии на втором этапе основано на следующих принципах:
после каждого изменения значения математического ожидания т. е. удачного шага оптимизационного процесса, дисперсия принимает свое первоначальное значение, что позволяет возобновить квазиравномерный поиск по i-й координате допустимой области;
если очередной k-й шаг не привел к уменьшению целевой функции (Mξik+1=const), то дисперсия определяется по формуле
![]()
где kу — коэффициент уменьшения дисперсии.
Коэффициент уменьшения дисперсии оказывает первостепенное влияние как на сходимость процесса к решению, так и на скорость сходимости. При больших k7 сокращается продолжительность расчета, однако уменьшается вероятность нахождения глобального экстремума; при малых ky — наоборот. Многочисленные практические расчеты позволяют дать оценку оптимального интервала этого коэффициента: kу=1,001-1,005 при оптимизации по народнохозяйственным затратам и kу=1,01—1,02 при оптимизации по стоимости трансформатора.

Рис. 4.18. Распределение 30 случайных точек, завершающих оптимизационный процесс проектирования трансформатора ТМ-1600/35

Рис. 4.19. Укрупненная схема алгоритма расчета трансформаторов методом случайного поиска
В табл. 4.5 приведены математические ожидания числа сочетаний ω, необходимых для разового обращения к математической модели по ходу оптимизационного процесса. Из таблицы видно, что по мере приближения к экстремуму вероятность вхождения в допустимую область P(D) увеличивается, что объясняется определённой локализацией зоны поиска.
Таблица 4.5

Останов процесса происходит при достижении условия
p{Xi=xi*") при ί=1, 2,...7, (4.51)
что наблюдается при достаточно большом сгущении вероятности поиска около экстремума, когда повторный выбор оптимальной точки х* становится единственно возможным событием. Эта ситуация при оптимизации трансформатора ТМ-1600/35 показана на рис. 4.18 при 30 завершающих обращениях к математической модели. Кружками обозначены оптимальные точки. Укрупненная схема алгоритма оптимизационного процесса на основе случайного поиска приведена на рис. 4.19.

