Метод оптимального проектирования представляет процедуру поиска оптимального решения, которая выражается в проведении испытаний в точках Хк, k=1, 2, ..., N. Оптимальное решение находится с помощью рекуррентных соотношений, записываемых для заданного начального приближения Χ1 в виде
(4.30)
После проведения N испытаний (итераций, обращений к математической модели объекта) оптимизационный процесс заканчивается или в связи с удовлетворением заданной точности решений, или в результате использования выделенного ресурса времени. Оптимальные значения критерия эффективности и регулируемых параметров определяются из условия
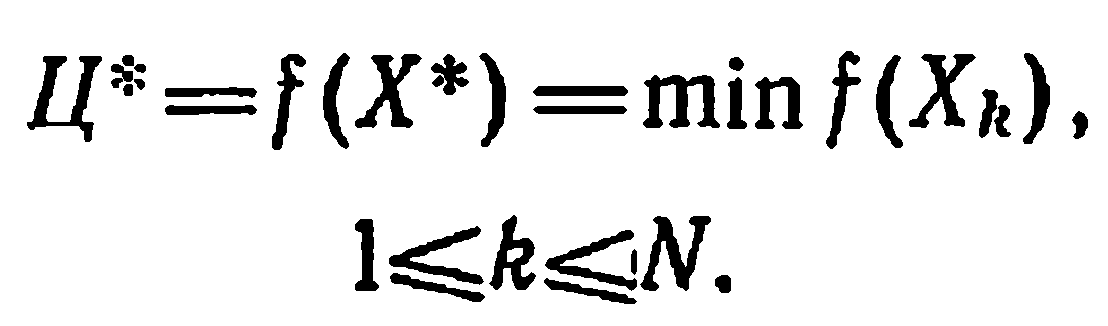(4.31)
Выражения (4.30) и (4.31) являются математической записью метода оптимального проектирования. Способ определения начальной точки и совокупность функций {Мk}характеризуют соответствующий алгоритм поисковой оптимизации [66].
Выполненный выше анализ характера задачи оптимизации трансформаторов значительно сужает круг методов, применимых для ее решения.
Исследование ряда методов, потенциально пригодных для оптимизации трансформаторов, представляется необходимым по следующим причинам:
- При оценке методов по конкретному критерию эффективности возможно задание отношения предпочтения. Смена критерия изменяет упорядоченный ряд методов, приводя к другому отношению предпочтения между ними. Иными словами, один и тот же метод (алгоритм), как правило, не является оптимальным с точки зрения разных критериев.
- Оптимальное проектирование предполагает определение параметров и характеристик наилучшего варианта объекта в качестве частной задачи. При общем подходе понятие оптимальности эквивалентно минимуму суммарных потерь, вызванных затратами на вычисления, связанными с минимизацией функции f(X), и затратами, обусловленными несовпадением конечного результата с абсолютным экстремумом [67].
Минимизация функции суммарных потерь в условиях меняющегося характера проектирования (промышленное, исследовательское, учебное и т. д.) возможна с помощью разных методов (алгоритмов) поисковой оптимизации.
- Расширение класса проектируемых объектов создает необходимость в организации библиотеки алгоритмов оптимизации с целью выбора наиболее эффективного алгоритма при решении конкретной задачи, что особенно актуально для САПР.
Основные вычислительные методы поиска экстремума функции многих переменных можно разделить на две группы: детерминированного и недетерминированного поиска.
К группе детерминированных методов относятся так называемые методы вычислительной математики: итерационный, градиентный, релаксационный и некоторые другие.
Кроме того, сюда можно отнести метод, построенный на основе многошагового процесса с использованием основной идеи динамического программирования, который определяет вычислительный процесс в соответствии с уравнением (4.6).
К группе недетерминированных методов относятся метод простого перебора независимых переменных (метод сканирования), а также методы организованного (рационализированного) перебора. К этой же группе относится метод случайного поиска (метод Монте-Карло).
Наконец, существуют вычислительные процессы, синтезирующие различные методы, которые используются самостоятельно на различных этапах поиска оптимума.
Каждый из указанных методов имеет свои особенности, свои условия, при которых он может эффективно работать, свой диапазон действия, а также определенные достоинства и недостатки, которые могут усиливаться или ослабляться в зависимости от характера решаемой задачи, т. е. конкретных условий применения.
Использование классических методов оптимизации предусматривает такое математическое моделирование исследуемого объекта (трансформатора), при котором все интересующие нас взаимосвязи параметров и характеристик трансформатора описываются системой нелинейных уравнений (неравенств) или в виде расчетного алгоритма.
Решение полученной системы уравнений или алгоритма позволяет получить варианты трансформатора, соответствующие заданным техническим условиям на параметры и характеристики.
Технически приемлемые варианты сопоставляются по заданному технико-экономическому критерию с целью выбора оптимального варианта. В ряде случаев эти два процесса могут быть объединены с помощью специального минимизируемого функционала, учитывающего одновременно условие (4.1) и целевую функцию (4.3).
Все методы вычислительной математики, обеспечивающие решение нелинейных систем и поиск экстремального значения функции, построены, по существу, на итерационном процессе, с помощью которого решение целенаправленно (метод Ньютона, метод градиента и др.) или случайно (метод случайного поиска и др.) продвигается к оптимальному. Следует отметить, что применение классических методов вычислительной математики (кроме метода случайного поиска) целесообразно только лишь при определенных условиях. В частности, исследуемые функции должны быть дифференцируемы, а принятые варьируемые параметры — непрерывны; должна существовать возможность замены неравенств лимитирующих параметров равенствами. В случае замены дискретных рядов варьируемых параметров непрерывными полученные с помощью классических методов варианты рассматриваются только как теоретически оптимальные и требуют дальнейшего уточнения с применением заданных дискретных рядов. Однако замена совокупности дискретных значений каких-либо чисел на непрерывные функции возможна не всегда.
Количество шагов, необходимое для получения оптимального решения, зависит от вида функции, заданной точности решения и, в ряде случаев, от принятого начального приближения. Время поиска оптимального варианта при использовании аппарата классических методов математики благодаря направленности решения при организации вычислительного процесса бывает минимальным.
Несмотря на довольно жесткие ограничения, применение классических методов вычислительной математики при проектировании силовых трансформаторов оказывается не только возможным, но и необходимым; в первую очередь — при широком исследовании взаимного влияния параметров, геометрии и характеристик трансформатора с учетом заданных условий оптимальных зон параметров и геометрических размеров, при получении обобщенных характеристик, а также в ряде других случаев.
Детерминированный поиск оптимального варианта может быть также организован на основе идеи динамического программирования, которая заключается в том, что одновременный (одноэтапный) процесс выбора многих параметров заменяется многоэтапным процессом, при котором на каждом этапе осуществляется выбор одного или нескольких параметров. Этот метод позволяет найти глобальный оптимум при наличии локальных оптимумов, не требует непрерывности варьируемых параметров или дифференцируемости функций (4.1) и (4.2), позволяет в полной мере учесть дискретный характер переменных Xj. Единственным условием метода является то, что структура задачи не должна зависеть от числа шагов и должна быть возможной интерпретация задачи как «-шагового процесса принятия решения. Вычислительная эффективность метода заключается в том, что из рассмотрения исключаются все комбинации варьируемых параметров, не удовлетворяющие заданным условиям.
В связи с этим представляется целесообразным использовать идею динамического программирования, т. е. интерпретировать задачу в многошаговый процесс, сохранив итерационную вычислительную схему и перебор всех значений Xj. При таком построении на каждом этапе вычислительного процесса необходимо запоминать только те значения Xj, которые соответствуют текущему оптимальному значению функции выгоды. При многошаговой вычислительной процедуре с целью уменьшения времени расчета необходимо разработать комплекс мер по сокращению числа рассматриваемых вариантов на каждом этапе.
Другой альтернативой использования основного принципа метода динамического программирования является замена поиска глобального оптимума поиском на каждом этапе локальных оптимумов. В этом случае перебор всех значений Хj становится излишним, так как рассматриваются только те значения переменных, которые на каждом этапе ведут к улучшению целевой функции. Для повышения надежности метода поиск можно повторить несколько раз, начиная с различных начальных состояний Хj0.
Применение для проектирования трансформаторов недетерминированного поиска оптимального варианта методом простого перебора всех сочетаний переменных Xj не может быть признано удовлетворительным из-за большого числа рассматриваемых вариантов. Объем вычислительной работы и время расчета при простом переборе экспоненциально увеличиваются с ростом количества варьируемых переменных.
Однако при ограниченном числе переменных в определенных условиях использование метода простого перебора может оказаться удобным, так как метод позволяет найти глобальный оптимум и учесть дискретность варьируемых переменных. Данный метод, по существу, не предъявляет каких-либо требований к математической подготовке вычислительного процесса.
С целью реализации основных преимуществ метода перебора представляется целесообразным, как уже отмечалось выше, при составлении вычислительного процесса использовать многошаговый поиск оптимального решения с ограничением числа рассматриваемых вариантов с помощью специально разработанных мероприятий. Для реализации такого вычислительного процесса составляется математическая модель трансформатора, максимально приближенная по логике к инженерной методике расчета трансформатора. Составление математической модели на основе инженерной методики поверочного расчета трансформатора имеет свои положительные стороны: при составлении модели полностью используется многолетний опыт инженерного проектирования; в. математическую модель легко вносятся все изменения или дополнения; математическая модель сохраняет свою наглядность, психологически облегчая переход от ручного проектирования к машинному, поскольку математическая база не изменяется. Данный подход реализован в работах [109, 110], которые, по существу, являются одними из первых отечественных работ по промышленному проектированию трансформаторов на ЭВМ. Следует считать особенно перспективным использование при оптимальном проектировании силовых трансформаторов метода случайного поиска, при реализации которого может быть обеспечено, во-первых, составление математической модели также на основе инженерной методики расчета, во-вторых, учет дискретности варьируемых параметров, что позволяет считать, что метод удовлетворяет основным требованиям промышленного проектирования. Вместе с этим следует отметить, что метод не всегда обеспечивает хорошую сходимость результатов, особенно в области оптимума.
Перспективными представляются также разработанные в последнее время методы геометрического программирования, которые предполагают представление ограничений и целевой функции полиномами следующих видов:
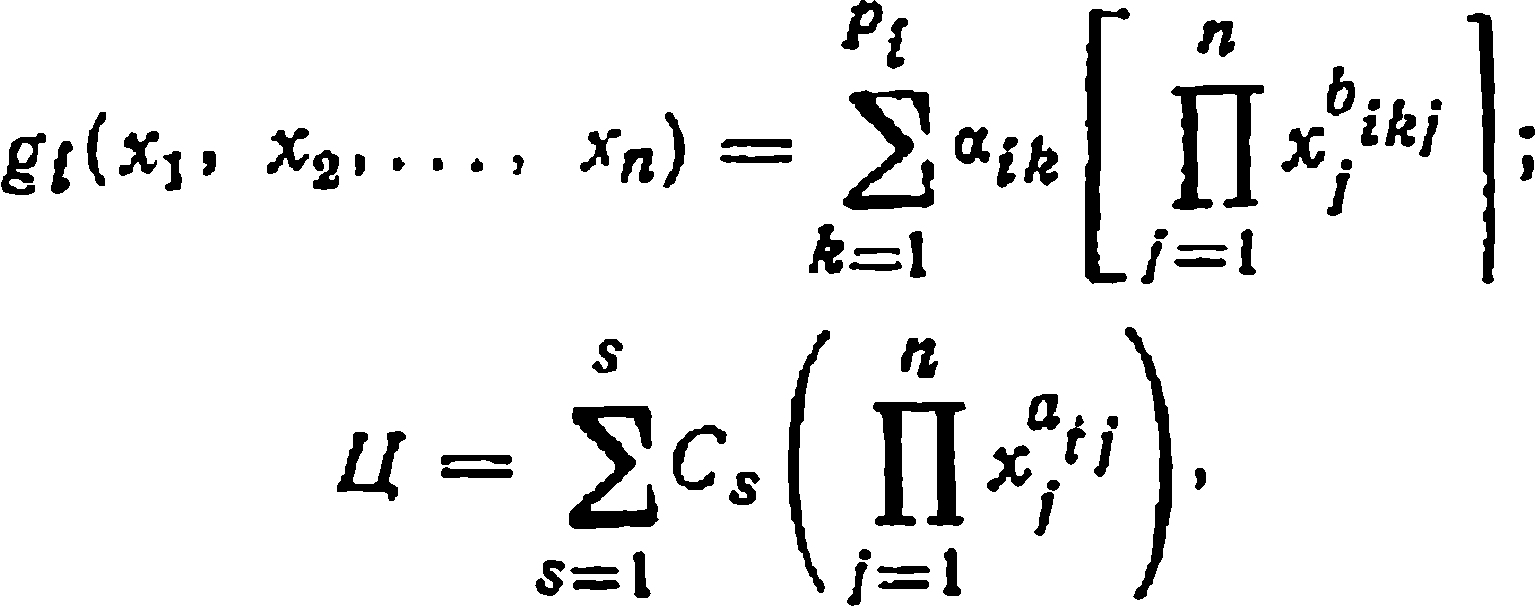
(4.32)
(4.33) где xj>0, аik>0 и Cs>0, bkjj и aii — произвольные вещественные числа.
В геометрическом программировании задача отыскания экстремума решается посредством преобразования исходной задачи в двойственную форму, что позволяет:
упростить вычисления, так как двойственные ограничения линейны, в то время как ограничения прямой задачи нелинейны; найти решение, поскольку минимум прямой функции равен максимуму двойственной.
Как видно из вышеизложенного, ни один из методов не обеспечивает гарантированного решения оптимизационных задач нелинейного программирования и не обладает только положительными свойствами. Можно отметить, что методы перебора и вычислительные процедуры с использованием приемов динамического программирования больше всего подходят к решению задач с явно выраженными дискретными переменными. Вместе с тем вычислительные трудности при использовании этих методов возрастают с ростом числа переменных, и в некоторых случаях из-за увеличения объема вычислительной работы они могут оказаться просто непреодолимыми для современных вычислительных машин. С другой стороны, методы, основанные на непрерывном представлении модели, позволяют целенаправленно проводить исследование этих
моделей и находить зоны оптимальных значений варьируемых переменных с высокой точностью и сравнительно небольшими затратами времени.
Выбор метода решения определяется характером задачи (необходимостью широкого исследования и поиска зон оптимальных решений, нахождением оптимального варианта внутри узкой зоны изменения переменных и т. д.), числом переменных, возможностями вычислительных машин и др. В ряде случаев находят применение синтезированные методы проектирования, в вычислительном процессе которых используется математический аппарат разных методов, и обеспечивается тем самым наибольший вычислительный эффект.
Примером синтезированного использования методов может являться двухэтапный процесс, когда на первом этапе с определенными допущениями (например, отказом от дискретности переменных) выполняется анализ всех взаимосвязей в трансформаторе. Это позволяет при незначительных затратах машинного времени установить с учетом заданных технических требований узкие оптимальные зоны варьируемых параметров. На втором этапе проектирования выполняются детальная раскладка обмоток трансформатора с учетом дискретности всех конструкторских элементов и поик оптимального варианта трансформатора на основе метода перебора. При этом варьируемые параметры изменяются в узких диапазонах, установленных на первом этапе проектирования, что значительно сокращает время расчета. В этом случае синтезированный метод оптимального проектирования позволяет реализовать на первом этапе основное достоинство непрерывных методов, т. е. быстроту нахождения и возможность поиска оптимального варианта в широком диапазоне изменения сочетаний параметров, а на втором этапе — достоинство метода перебора, т. е. учет дискретного характера всех конструкционных элементов и предельное приближение полученного варианта к промышленным условиям.
