Автоматизированное проектирование силовых трансформаторов - Оптимальное проектирование силовых трансформаторов методом рационализированного перебора

Требование дискретного изменения части или всех варьируемых параметров при оптимальном проектировании применительно к промышленным условиям является, как правило, необходимым условием разработки вычислительного процесса оптимизации любого устройства, в том числе и силового трансформатора. В частности, при проектировании силовых трансформаторов должен учитываться дискретный характер изменения диаметра стержня магнитопровода, числа катушек, числа витков в катушках, размеров обмоточного провода и т. д.

Решение дискретных задач проектирования имеет целый ряд принципиальных трудностей, в частности при дискретной оптимизации, как уже отмечалось, затруднено использование большинства классических методов оптимизации, основанных на дифференциальном исчислении. Поэтому основой дискретного проектирования может являться идея сканирования, базирующаяся на конечности числа рассчитываемых вариантов. Однако применение метода простого перебора, как правило, не представляется возможным из-за огромного объема вычислительной работы даже при относительно небольшом числе варьируемых переменных. Например, при четырех параметрах, каждый из которых может принимать 10 значений, число вариантов составит 104. При этом большая часть вариантов (сочетаний переменных), рассматриваемых в процессе решения, не удовлетворяет заданным условиям (4.1) или (4.2) и, следовательно, никакого влияния на выбор оптимального решения не оказывает. Отсюда вытекает главное требование, чтобы метод дискретного проектирования позволил возможно раньше исключить эти «балластные» сочетания варьируемых переменных из рассмотрения, что в значительной степени сократит число рассчитываемых вариантов и время поиска оптимального варианта.
При разработке дискретного метода оптимального проектирования целесообразно принять многоэтапную структуру метода динамического программирования, при которой на каждом этапе максимизируется целевая функция в зависимости от изменения только одной переменной. Другими словами, мы возвращаемся к методу перебора, организованного по определенной структурной схеме, которая с помощью многоэтапной процедуры моделирует взаимосвязи параметров и характеристик трансформатора. Такое решение обеспечивает максимальное использование имеющегося опыта инженерного проектирования и эффективность поиска оптимального варианта.
Метод, имеющий в своей основе организованный по определенной многоэтапной структурной схеме перебор переменных и предусматривающий уменьшение количества рассматриваемых вариантов за счет исключения не удовлетворяющих заданным условиям на проектирование, будем далее называть методом рационализированного перебора (РП).
Комплекс мер по сокращению числа рассматриваемых вариантов включает в себя:

1. Ограничение зоны изменения ряда независимых переменных технически обоснованными пределами, установленными на основе уже имеющегося опыта проектирования или в результате предварительных расчетов.
2. Использование проектных уравнений взаимосвязи основных параметров трансформатора с его геометрическими размерами для сокращения числа независимых переменных и нахождения функциональных зависимостей между переменными путем решения проектного уравнения.
3. Введение различных проверок технического состояния трансформатора на разных, возможно более ранних стадиях расчета, что также позволит исключить из дальнейшего рассмотрения неудовлетворительные результаты.

Ограничение зоны изменения ряда переменных относится, в первую очередь, к диаметру стержня магнитопровода dc, индукции в стержне Вс и плотности тока в обмотках δ1 и δ2. При проектировании трансформатора, используя сведения об аналогичных типах и сериях, инженер достаточно точно может указать несколько соседних диаметров в нормализованной шкале, которые обеспечат нахождение оптимального варианта трансформатора; при отсутствии оптимума в принятом диапазоне осуществляется автоматический сдвиг при выборе нового значения dc по нормализованной шкале не более чем на один шаг в Ту или иную сторону. Выбор зоны изменения индукции в стержне магнитопровода и плотности тока в обмотках зависит от мощности и типа проектируемого трансформатора и в большинстве случаев достаточно хорошо известен из практики проектирования.
В качестве основного проектного уравнения связи целесообразно принять уравнение для индуктивного сопротивления обмоток, поскольку проектирование силовых трансформаторов, как правило, выполняется на заданное значение напряжения КЗ. При выборе плотности тока в обмотках по заданному превышению температуры, а не из технико-экономических соображений (минимуму годовых затрат) возможно использование также уравнения теплового баланса обмоток. В ряде случаев в зависимости от конкретных условий могут использоваться и другие уравнения. Применение проектных уравнений связи позволяет формализовать зависимость между варьируемыми переменными с помощью заданного технического параметра (напряжения КЗ, превышения температуры обмоток и др.), исключить из рассмотрения сочетания переменных, не удовлетворяющие этому уравнению, а следовательно, заданным условиям проектирования.
Весьма эффективным средством сокращения объема перебора является введение в алгоритм проверок по некоторым техническим характеристикам или параметрам (по сортаменту обмоточного провода, плотности тока, току XX, геометрии трансформатора и т. д.). Проверки проводятся с помощью неравенства, устанавливающего связь этого параметра с варьируемыми независимыми переменными.
Таким образом, метод рационализированного перебора, являющийся дальнейшим развитием дискретных методов оптимального проектирования силовых трансформаторов, характеризуется:

1. Многоэтапной структурой вычислительного процесса, который составляется на основе концентрических циклов по варьируемым переменным.
2. Логическим построением многоэтапного процесса, максимально соответствующего инженерной методике расчета силового трансформатора.
3. Значительным сокращением по сравнению с простым перебором числа рассматриваемых вариантов за счет: использования проектных уравнений взаимосвязи;

применения неравенств-лимитеров, позволяющих проводить проверки по отдельным, наиболее характерным техническим параметрам на соответствие их заданным условиям;
ограничения диапазонов изменения варьируемых независимых переменных в технически обоснованных пределах.
Организация вычислительного процесса на основе метода РП обеспечивает рассмотрение всех технически приемлемых вариантов трансформатора и выбор среди них оптимального с учетом заданного технико-экономического критерия.
Будем рассматривать оптимизационный процесс на основе перебора вариантов как некоторый ветвящийся процесс (рис. 4.8), идущий таким путем, что в начальный момент задается исходная система величин, а в каждый следующий момент из нее может образовываться несколько новых систем величин. Полученное таким образом множество развивается аналогично, порождая для каждого своего элемента соответствующее подмножество и т. д; Назовем корнем узловую точку ветвящегося процесса, в которую входит одна ветвь предшествующего этапа и выходит R альтернатив. Общее количество ветвей процесса на n-м этапе (полное число рассчитываемых вариантов) будет равно R(n), а общее количество ветвей «дерева» определяется по формуле [112]
(4.34)
Коренным отличием РП от простого перебора является свойство селективности, под которым понимается следующее: система величин (совокупность вариантов), получаемая на каком-то этапе процесса, оценивается в соответствии с некоторыми эмпирическими критериями и разбивается на две подсистемы: А и Б — удовлетворяющую и неудовлетворяющую этим критериям; в последующем подсистема Б исключается из рассмотрения. Свойство селективности метода РП позволяет ограничить разнообразие возможных продолжений (тем самым сократить пространство поиска) и выйти на те ветви, которые ведут к возможному решению.

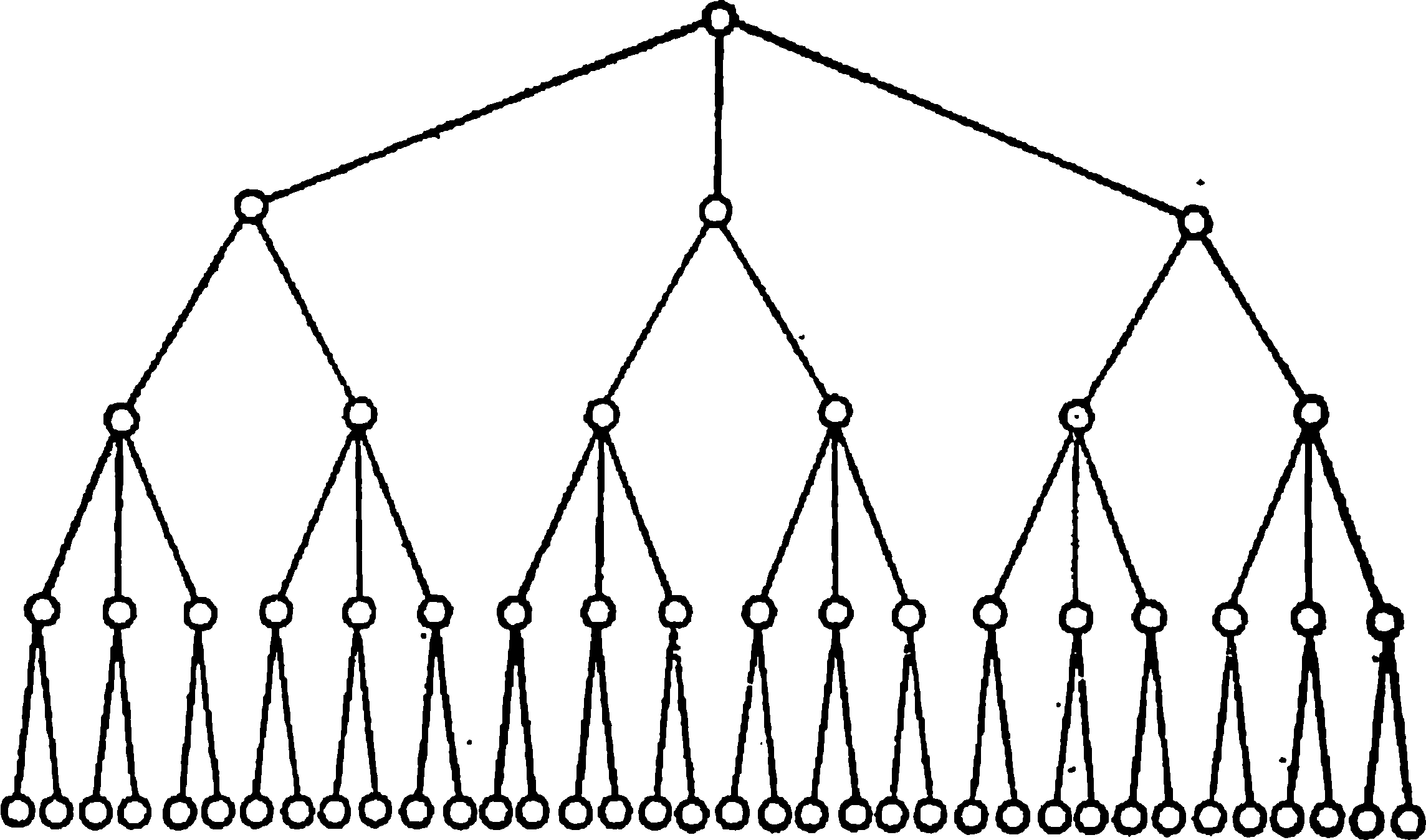
Рис. 4.8. Ветвящийся процесс, соответствующий полному перебору вариантов

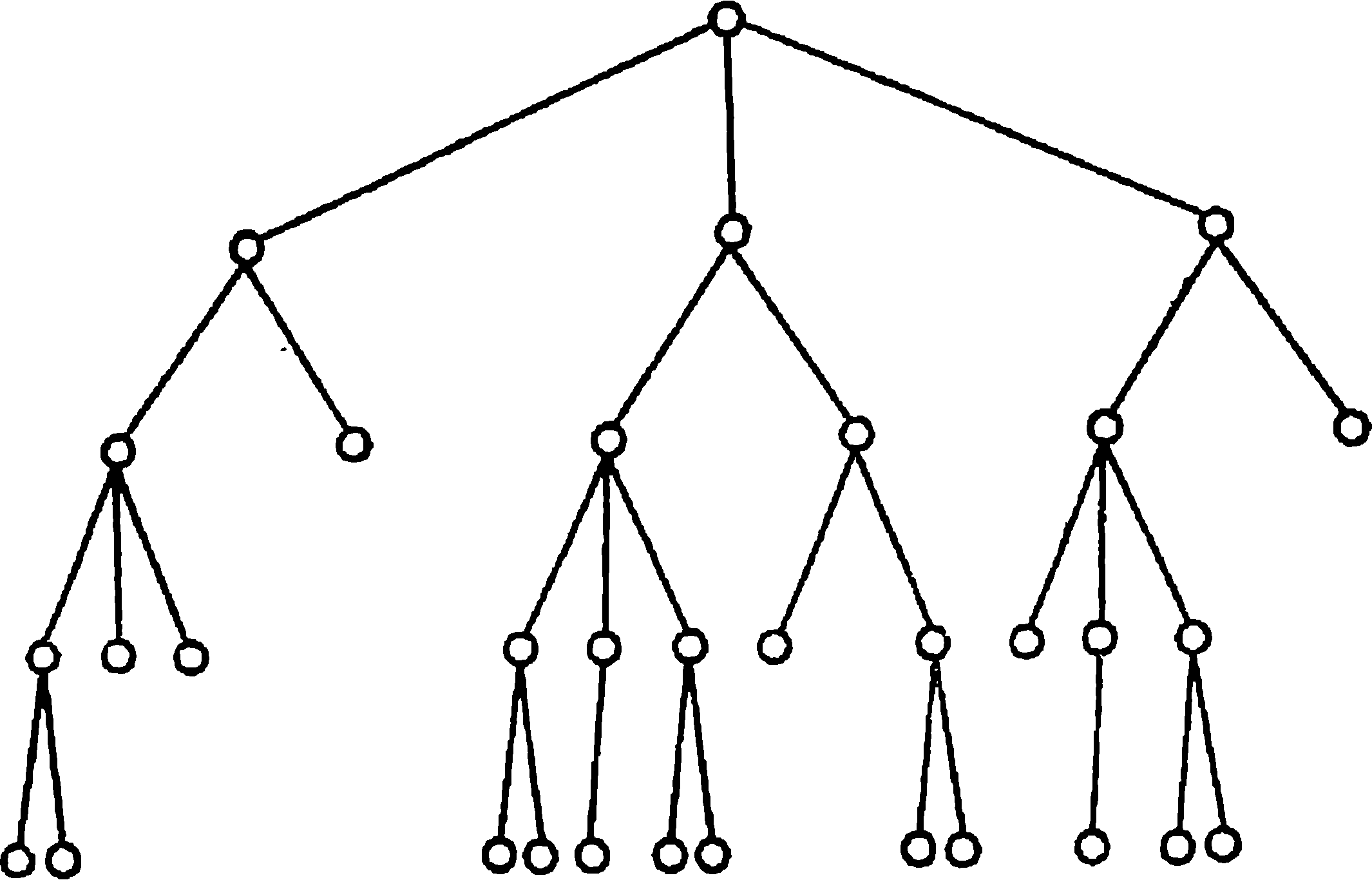
Рис. 4.9. Усеченный ветвящийся процесс, соответствующий рационализированному перебору вариантов

Однако подобные ограничения могут, с одной стороны, в подсистему А отнести и те продолжения, которые не ведут к цели (что, как правило, неизбежно), с другой стороны, отсечь ветви, по которым можно было бы прийти к оптимальному варианту. Последнюю возможность в методе РП обычно исключают увеличением подсистемы А за счет подсистемы Б. Эвристический характер процесса обусловлен тем, что эмпирические критерии, полученные на основе опыта, образуются в условиях неполной информации о характере процесса и, следовательно, являются не истинными, а лишь правдоподобными.
Граф, полученный в методе РП, называют усеченным ветвящимся процессом (рис. 4.9), эффективность построения которого можно определить аналитически, Пусть т1, т2,...,тп — количество отсеченных корней ветвящегося процесса на соответствующем этапе решения. Тогда количество ветвей на этих этапах будет равно
(4.35)

Суммируя (4.35) и преобразуя, получаем общее количество реализуемых ветвей оптимизационного процесса, которое может быть интерпретировано как длина пути, ведущего к решению (с учетом, что /„*и=0, если решение достигнуто на n-м этапе):
(4.36)
Эффективность метода РП Э(п) может быть определена как отношение длин путей к решению без использования эвристик U и с их использованием L, Тогда с учетом (4.34) и (4.35) имеем
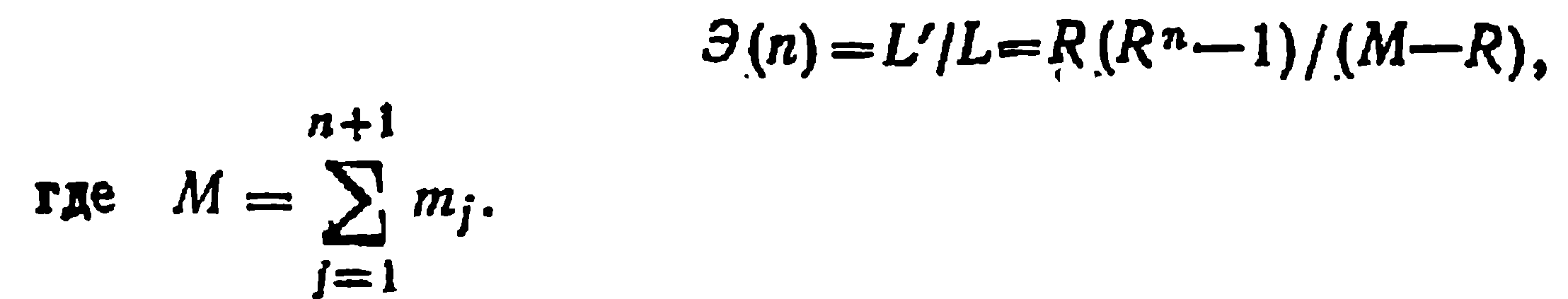(4.37)

Учитывая, что Mmin=(R—1)n+R и Mmax=Rn+1, получаем пределы изменения эффективности поиска на основе метода РП
(4.38)
Очевидно, что случай Э(n) = 1 соответствует полному перебору вариантов.
Построение вычислительного процесса на основе метода РП осуществлялось в соответствии с вышеизложенными теоретическими положениями. При этом в качестве задачи оптимизации рассматривалась задача промышленного проектирования силовых масляных трансформаторов класса 35 кВ, которая имеет две разновидности: оптимизационный расчет типоисполнений трансформаторов и общую задачу оптимального проектирования.
Под общей задачей оптимизации трансформаторов будем понимать нахождение такого сочетания всех варьируемых параметров из дискретного набора, приведенного в § 4.3, которое при заданных ограничениях обеспечивает наименьшее значение целевой функции.
При организации вычислительного процесса на ЭВМ на основе метода РП основной задачей, как указывалось выше, является значительное сокращение количества рассчитываемых вариантов. Для этого всем варьируемым параметрам поставлен в соответствие исходный ограниченный диапазон изменения, содержащий ряд дискретных значений (табл. 4.1).
Следующим шагом на пути сужения зоны поиска экстремума является замена неравенств (4.9) и (4.10) равенством ввиду небольшого значения установленного расчетного допуска на этот параметр.
Та блица 4.1

Напряжение КЗ является важнейшим эксплуатационным параметром трансформатора, допустимое значение которого жестко ограничивается при проектировании. Значение напряжения КЗ в значительной степени определяет геометрию трансформатора средней и большой мощности, так как для них напряжение КЗ практически определяется реактивной составляющей uк.р, т. е. uk.р≈Uk.
В связи с этим целесообразно использовать математическую связь с номинальными параметрами трансформатора и его основными геометрическими размерами (диаметр стержня магнитопровода, радиальные размеры обмоток и др.) с целью ограничения числа рассматриваемых вариантов только теми, которые удовлетворяют заданному значению ик.
С этой целью воспользуемся уравнением для напряжения КЗ
(4.39) где

Преобразуя (4.39) относительно радиального размера обмотки 0,2) получаем уравнение связи между радиальными размерами обмоток а1 и а2 при заданных номинальных параметрах трансформатора Рн и Iф1 выбранном диаметре магнитопровода dc, заданном % и принятых основных изоляционных расстояниях а01 и а12. Это позволяет вывести из числа варьируемых параметров ширину провода обмотки ВН, которая определяется из найденного размера а2. После округления а'пр2 до табличного значения значение ик проверяется на удовлетворение заданному исходному значению.
Неравенство
(4.40)
также использовано в виде равенства Н1=Н2, так как значение ∆Н можно получить равным нулю за счет различной степени прессовки обмоток. Это дает возможность определять высоту провода обмотки ВН исходя из известной высоты обмотки НН. После округления полученного значения bпр2 до табличного высоты обмоток выравниваются с точностью до ∆Н в результате разгонки горизонтальных каналов. Таким образом, замена неравенств равенствами позволяет сократить число варьируемых параметров до восьми.
Таблица 4.2

Использование других неравенств математической модели трансформатора для связи варьируемых параметров и уменьшения их числа, как правило, оказывается необоснованным и в общем случае может исключить нахождение глобального экстремума.
Полное число вариантов, которое получается при изменении восьми регулируемых параметров в установленных диапазонах, оценивается значением порядка 6-108. В табл. 4.2 показана полученная в процессе исследования алгоритма РП эффективность использования логических операторов, осуществляющих отсев вариантов, неудовлетворяющих заданным условиям или заведомо неэкономичных.
Следует отметить, что применяемые для ограничения области поиска логические операторы имеют неодинаковую природу. Их можно разделить на следующие три группы:

1. Операторы, обеспечивающие удовлетворение нормативных требований, соответствующие ограничениям (4.9) — (4.19), формирующим допустимую область. Введение их в логическую схему поиска в любом случае является обязательным.
2. Операторы, обусловливающие конструктивную и технологическую реализуемость проектируемого объекта. Вид и число этих операторов зависят от условий конкретного производства.
3. Операторы, полученные на основе инженерного опыта проектирования и анализа существующих конструкций. Эти операторы имеют эвристическую природу и свойственны методу РП. Представляется, что за счет совершенствования именно этой группы операторов метод РП имеет перспективы дальнейшего развития.

Как видно из табл. 4.2, основная функция логического аппарата, включающего все операторы из отмеченных групп, — вывести из рассмотрения максимальное количество вариантов на возможно ранних стадиях расчета — выполняется удовлетворительно, так как к концу первой половины вычислительного процесса отсеву подвергается 99% существующих вариантов.
На рис. 4.10 приведена укрупненная схема алгоритма расчета трансформаторов методом РП. Расчет начинается с ввода в ЭВМ исходных данных оптимизируемого трансформатора и определения параметров, сохраняющих на протяжении всего расчета постоянные значения. Затем организуются концентрические циклы по перебору варьируемых параметров, охватывающие основные расчетные блоки.
Наиболее сложный в логическом отношении алгоритм раскладки обмоток детализирован на рис. 4.11. На этом этапе вычислительного процесса выполняются следующие основные операции:
определяется число витков в катушке обмотки ВН (блоки 1—4);
проверяется соотношение между числом витков в основных и регулировочных катушках обмотки ВН (5—8);
определяется высота провода обмотки ВН (10—13);
выравниваются высоты обмоток за счет изменения соотношения увеличенных и нормальных каналов (14—20);
определяются радиальный размер обмотки ВН и ширина провода этой обмотки (21—33).

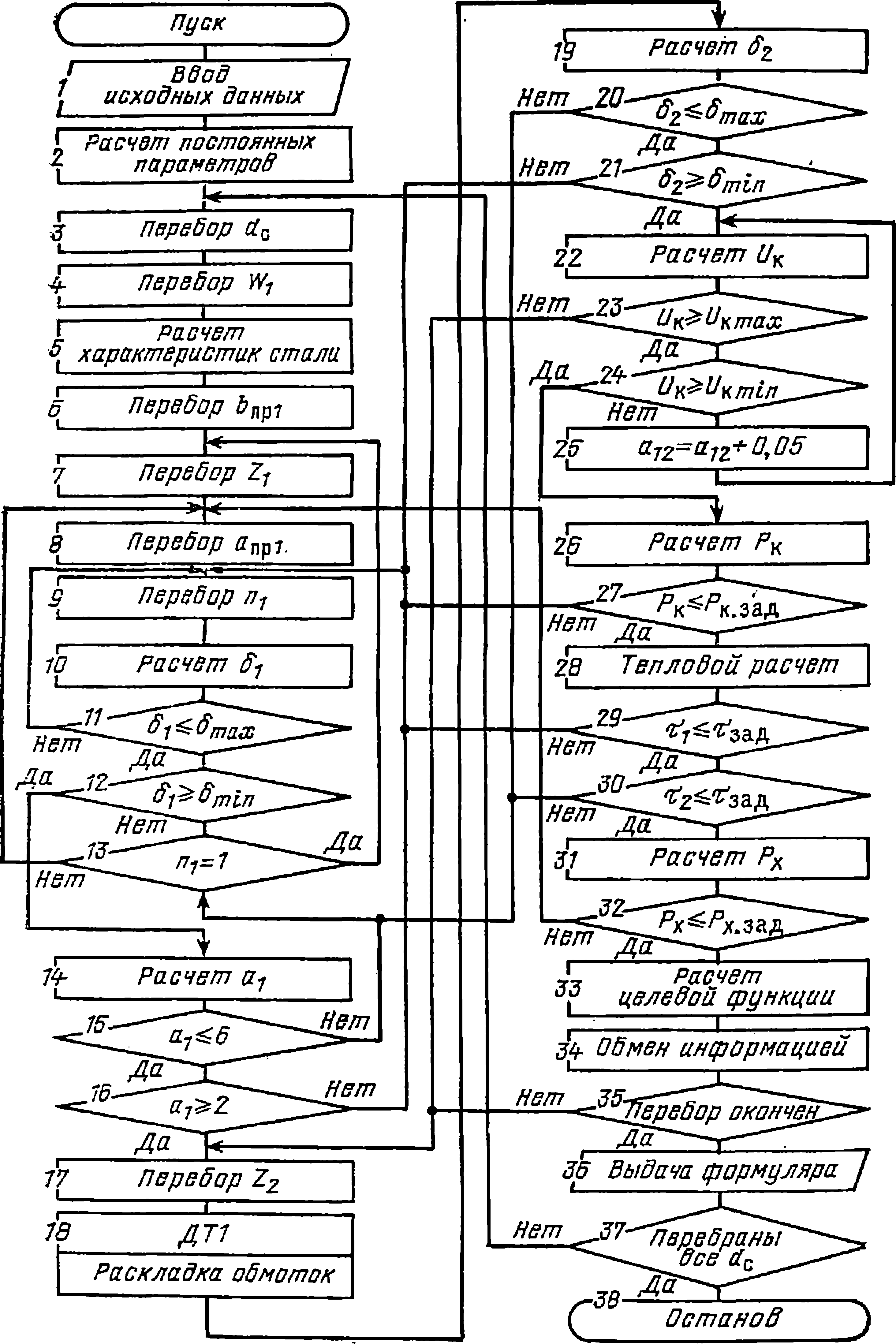
Рис. 4.10. Укрупненная логическая схема алгоритма оптимизации трансформаторов методом рационализированного перебора

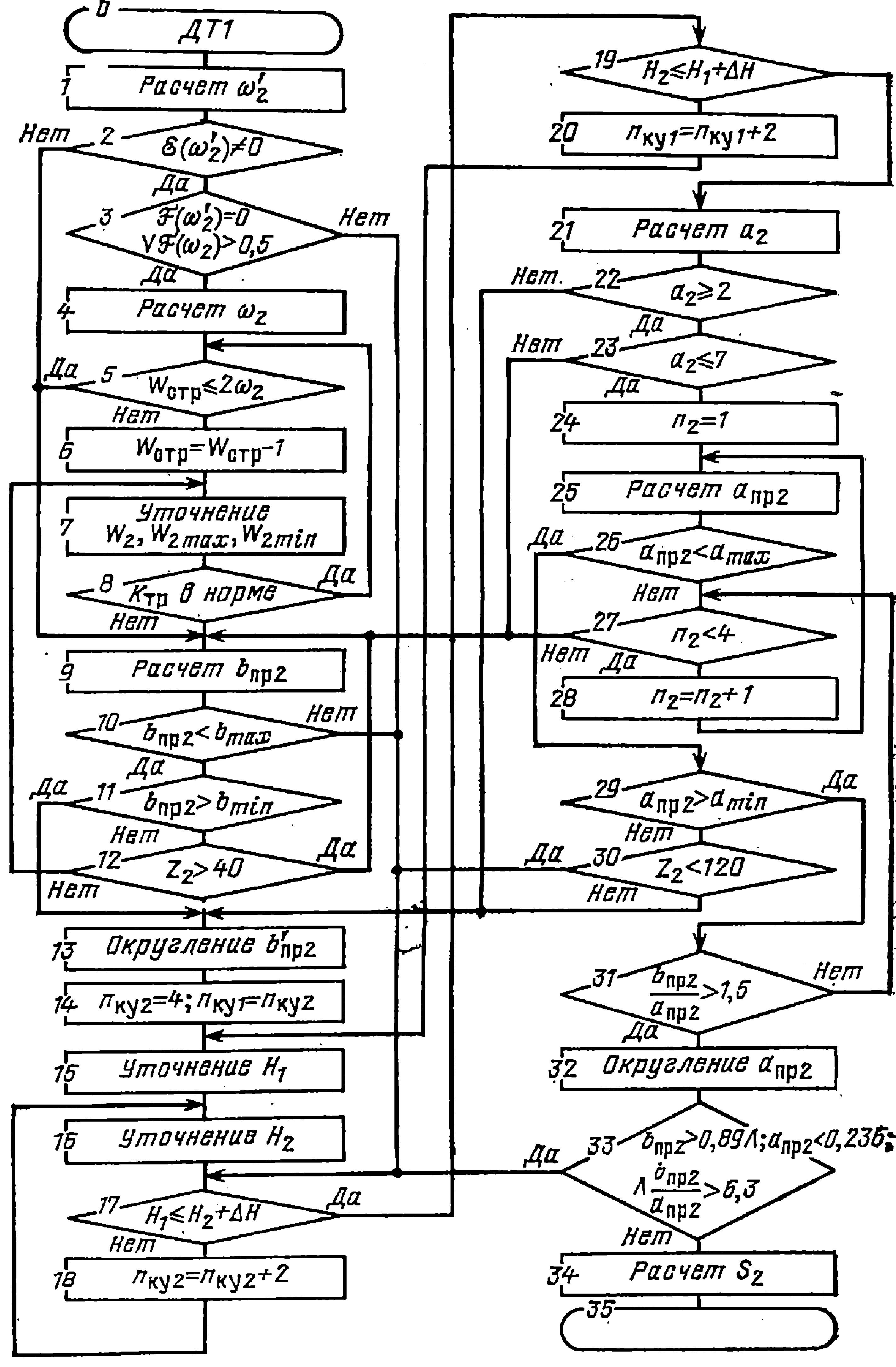
Рис. 4.11. Расчет и раскладка непрерывных катушечных обмоток

При разработке вычислительного процесса в связи с пологим характером целевой функции вблизи экстремума была предусмотрена возможность выдачи на печать не одного оптимального варианта, а группы наилучших вариантов, имеющих близкие по значению экономические показатели, но различное конструктивное исполнение. Это позволяет при инженерном анализе находить лучший вариант при сложившихся производственных условиях.