Гидравлические нестационарные процессы в жидкометаллических контурах при принудительной циркуляции теплоносителя слабо зависят от его температуры. Это объясняется в первую очередь небольшими изменениями плотности натрия, сплава натрий-калий и других жидких металлов в широком диапазоне температур. В связи с этим и расчетные, и экспериментальные исследования процессов изменения расходов теплоносителя в контурах чаще всего могут проводиться независимо от процессов изменения температур.
Учет температурных условий становится необходимым на таких уровнях расхода, когда гидравлическое сопротивление контура приближается к напору естественной циркуляции при заданном распределении температур в нем. О таких режимах работы установок речь пойдет ниже.
Рассмотрим вначале соотношения, с помощью которых можно рассчитывать изменения во времени расхода теплоносителя при нарушениях работы циркуляционных насосов.
Система уравнений для расчета гидравлических переходных процессов в контурах включает в себя уравнения движения теплоносителя, роторов насосов, обратных клапанов и др.
Приведем эту систему уравнений в упрощенном виде. Уравнения движения теплоносителя в теплоотводящих петлях:
![]()
Здесь Gi — расход теплоносителя i-й петле, отнесенной к номинальному значению; Δρi - гидравлическое сопротивление теплоотводящих петель на их индивидуальных участках; ΔΡ - гидравлическое сопротивление общего участка всех петель - реактора; Hi - напор i-го насоса; параметр
![]()
где ljj, fjj - длина и площадь проходного сечения i-го участка в i-й петле соответственно; G0i — начальный массовый расход теплоносителя в петле. Суммирование проводится последовательно по всем участкам петли:
Выражение (175) записано в предположении, что положение обратного клапана в петеле сохраняется неизменным. В противном случае необходимо учитывать изменение его коэффициента сопротивления.
Расход теплоносителя через реактор
![]()
где к - число теплоотводящих петель в первом контуре. Уравнения (174) описывают второй закон Ньютона применительно к теплоносителю в петлях.
![]()
Аналогичным образом получаются уравнения движения роторов. Постойная времени теплоносителя определяется по (180). Нужно отметить, что в рассматриваемом случае при подстановке в это соотношение гидравлическое сопротивление контура должно включать в себя помимо прочих компонент сопротивление собственно насоса. Для иллюстрации приведем на рис. 36 изменение расхода натрия в первом контуре реактора БР-10 при отключении обоих электромагнитных насосов контура. Это изменение хорошо описывается гиперболой с постоянной времени 0,2 с.
Если отключаются не все, а лишь отдельные насосы первого контура, то их выбег не является свободным. Противодавление на выходе, создаваемое оставшимися в работе насосами, существенно влияет на этот выбег.
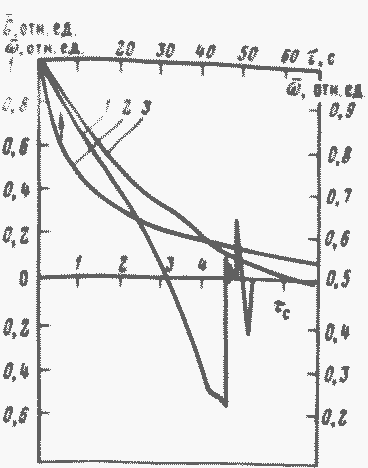
Рис. 37. Отключение одного насоса первого контура из пяти:
1 - расход натрия в отключенной петле; 2. 3 - частота вращения насоса в отключенной петле падение скорости его вращения. Проходное сечение для теплоноси. теля в реакторе, приходящееся на одну работающую петлю, возраста, ет. Гидравлическое сопротивление контура падает, а производительность оставшихся в работе насосов увеличивается. Через некоторое время расход в отключившейся петле падает до нуля, а затем становится отрицательным, т.е. теплоноситель в петле начинает течь в направлении, противоположном нормальному. Это вызывает закрытие обратного клапана, после чего расход в петле снова становится равным нулю. Максимальное значение обратного расхода, развивающегося в петле в процессе закрытия обратного клапана, определяется характеристиками последнего.
На рис. 37 построены графики изменения расхода натрия и частоты вращения насоса в отключившейся петле реактора БН-350. Из графиков видно, что расход натрия в отключившейся петле падает до нуля за 3,2 с. Частота вращения отключившегося насоса падает медленнее, чем при свободном выбеге. Расход четырех оставшихся в работе насосов первого контура возрастает на 11-12 % исходного. Поэтому расход натрия через реактор после отключения петли падает лишь на 11 % номинального. Кривые показывают также, что в процессе закрытия обратного клапана в петле развивался довольно значительный обратный расход натрия. Это объяснялось большим сопротивлением гидравлического тормоза, которым был снабжен клапан. После его переделки обратный расход, возникающий при закрытии, существенно снизился.
Можно получить простое приближенное аналитическое решение для расчета гидравлического переходного процесса в первом контуре при отключении одного циркуляционного насоса.
Перепишем (177) в совокупности с (179) для отключенного насоса следующим образом:
![]() (182)
(182)
Отключенной петле для определенности присвоен индекс 1.
Обозначим время падения расхода теплоносителя в отключившейся петле до нуля Δ и приближенно положим для т < Δ
![]()
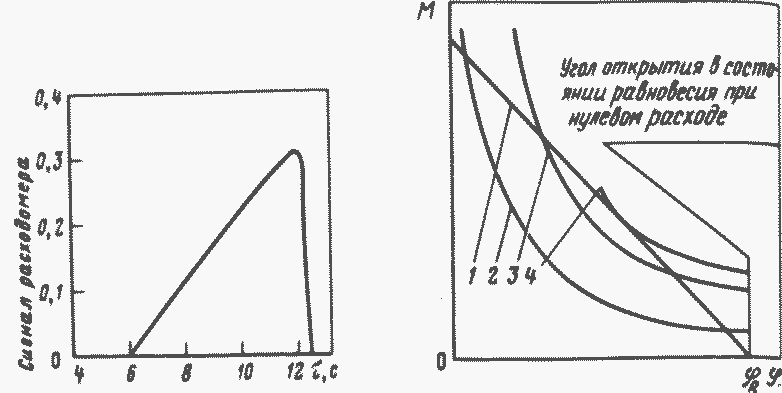
Рис. 38. Изменение сигнала расходомера при открытии запорной задвижки в петле первого контура и появлении в ней обратного расхода натрия
Рис. 39. Зависимость моментов сил, действующих на обратный клапан, от его углового положения при различных расходах теплоносителя:
1 - момент силы тяжести; 2, 3, 4 - моменты сил, обусловленных перепадом давления на клапане при возрастающих обратных расходах в критический расход теплоносителя
При записи этих выражений предполагалось, что число работающих петель т в общем случае не равно номинальному их числу к. Частоты вращения всех работающих насосов ω, заданы одинаковыми. Для реактора БН-350 отключение одного насоса первого контура из пяти приводит, как уже говорилось, к увеличению расхода натрия в работаюп^их петлях на 11%, отключение двух насосов - на 22 % номинального, G падаете первом случае до 0,89, во втором - до 0,73.
Полезно кратко остановиться на работе обратного клапана, установленного на выходе насосов первого контура. В реакторе БН-350 было замечено, что при росте обратного расхода натрия в различных условиях клапан закрывается при одном и том же критическом значении расхода. Такой процесс можно наблюдать, например, при открытии запорной задвижки в отключенной петле, когда насосы в других петлях контура уже работают. При этом обратный расход в петле медленно возрастает до 20-24 % номинального, затем резко падает до нуля при закрытии клапана (рис. 38).
Показано, что закрытие клапана происходит при нарушении устойчивости его положения в потоке теплоносителя. В положении равновесия при нулевом расходе теплоносителя в петле клапан открыт на угол, достаточный для того, чтобы клапан не мешал развитию естественной циркуляции теплоносителя в петле. При отклонении клапана от положения равновесия за счет обратного потока теплоносителя на клапан действуют моменты силы тяжести и силы, обусловленной перепадом давления на нем. Зависимость этих моментов от угла поворота клапана и расхода теплоносителя в петле показана на рис. 39. Рисунок поясняет также, при каком расходе, названном критическим, нарушается устойчивость положения клапана в потоке теплоносителя и он закрывается. Критический расход теплоносителя представляет собой максимальный расход, при котором еще возможно равенство моментов указанных сил. действующих на клапан. Перепад давления на петле, соответствующий критическому расходу, не совпадает с перепадом давления, который достаточен для удержания клапана в закрытом состоянии. Критический расход теплоносителя снижается при уменьшении доли гидравлического сопротивления реактора в общем гидравлическом сопротивлении первого контура. Измерение критического расхода теплоносителя в натурных условиях позволяет косвенно определить гидравлическое сопротивление клапана при малых углах открытия. Измерения при таких углах в стендовых условиях могут оказаться затруднительными из-за больших перепадов давления на клапане.
В некоторых режимах работы могут возникать колебания обратного клапана в потоке теплоносителя и при нормальном направлении его течения в петле. Колебания клапана вызывают периодические изменения расхода теплоносителя. Такие колебания возможны при малых расходах из-за немонотонности в некоторых диапазонах угла открытия клапана зависимости его гидравлического и лобового сопротивления от этого угла в нестационарных условиях.
Гидравлические параметры реактора, циркуляционных насосов, контуров, обратных клапанов, необходимые для расчета переходных процессов, определяются в проектных расчетах, в стендовых экспериментах и проверяются в натурных испытаниях непосредственно на реакторе. В частности, в натурных испытаниях уточняются постоянные выбега насосов, параметры их комплектных характеристик, которые не всегда возможно измерить на стендах, гидравлическое сопротивление реактора и контура в целом, инерционные параметры контуров, зависимость движущего момента на валу насоса от скорости его вращения.
Например, измерив закон снижения оборотов одного отключенного насоса первого контура после закрытия обратного клапана, можно определить момент сопротивления на его валу при нулевом расходе. Запись оборотов того же насоса при запуске на закрытый обратный клапан дает материал для определения зависимости движущего момента от скорости вращения. Измерение оборотов опять-таки одного отключенного насоса в момент закрытия его обратного клапана позволяет найти расчетом по (184) гидравлическое сопротивление реактора. Напор насоса при нулевом расходе можно считать заданным, так как характеристика насоса в основном квадранте всегда известна по результатам стендовых испытаний.
До сих пор речь шла о режимах принудительной циркуляции теплоносителя, когда напор естественной циркуляции пренебрежимо мал по сравнению с напором насосов.
Напор естественной циркуляции в замкнутом контуре
![]() (189)
(189)
где l - координата в контуре в направлении течения теплоносителя;
pNa - температура и плотность теплоносителя соответственно; φ угол между вектором скорости теплоносителя в элементе dl и вертикалью. Для натрия dp/ dr = 0,24 кг/ (м3-К).
Номинальные перепады температур в первом и втором контурах составляют около 200 °C. Поэтому даже в том простейшем случае, когда контур состоит из двух вертикальных ниток - холодной и горячей высотой, например, 10 м, соединенных горизонтальными перемычками движущий напор естественной циркуляции в нем достигает лишь 570 мм натриевого столба. Для сравнения можно сказать, что напор насоса первого контура на оборотах, составляющих лишь 10 % номинальных обычно превышает 1 м натриевого столба. Поэтому термический напор естественной циркуляции начинает оказывать влияние на движение теплоносителя практически только после остановки насоса.
Система уравнений для расчета режимов естественной циркуляции наряду с уравнениями движения теплоносителя должна включать в себя уравнения, описывающие изменения температур на всех участках контура Приближенные экспресс-расчеты переходных режимов естественной циркуляции, которые можно осуществить вручную, не имеют ценности из-за неизбежно низкой точности. Поэтому сделаем здесь лишь некоторые замечания о стационарных режимах естественной циркуляции. Основной вклад в гидравлическое сопротивление в первом контуре в таких режимах дает трение в ТВС:
![]() (190)
(190)
где Нтвэл - высота твэла; dг - гидравлический диаметр каналов активной зоны.
Для таких условий расход естественной циркуляции в контуре пропорционален корню квадратному из мощности энерговыделения. Коэффициент пропорциональности можно получить с помощью (189), (190) и соотношения, связывающего подогрев теплоносителя в реакторе с его мощностью. Если гидравлическое сопротивление контура имеет квадратическую зависимость от скорости теплоносителя, что бывает при большой доле местных сопротивлений в нем, то расход естественной циркуляции пропорционален корню кубическому из мощности реактора.

