Изменение температур в активной зоне реактора на быстрых нейтронах в переходных процессах. Следующая из упоминавшихся выше задач, которые приходится решать при исследовании переходных процессов в ЯЭУ, состоит в определении зависимостей температур всех основных ее элементов от времени. В связи с этим возникает необходимость анализировать процессы нестационарной теплопроводности, конвективного теплообмена, теплообмена излучением в реакторе, теплообменных аппаратах, трубопроводах, смесительных камерах, газовых объемах. Во многих случаях задачи нестационарного теплообмена могут решаться независимо, а в некоторых из них - в совокупности с задачами нестационарной гидродинамики. В нижеследующих разделах описаны простые модели для оценки параметров указанных процессов, проиллюстрировано применение таких величин, как постоянные времени твэла, плоской стенки, смесительной камеры, а также таких часто употребляемых динамических характеристик, как передаточная функция, импульсная и разгонная характеристики.
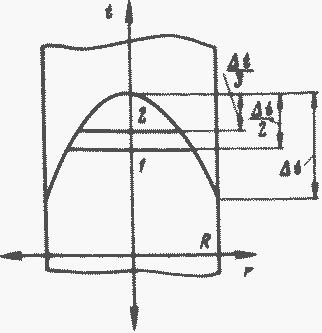
Вначале рассмотрим стационарное температурное поле в неограниченной пластине и бесконечном цилиндре с тепловыделением (рис. 22). Это температурное поле определяется из решения стационарного уравнения теплопроводности:
для цилиндра радиусом R
![]()
(58)
для плоской стенки толщиной R
![]()
(59)
Зададим температуру на поверхности цилиндра или пластины:
![]() (60)
(60)
Температура в центре цилиндра удовлетворяет условию симметрии:
![]()
Рис. 22. Стационарное распределение температуры в пластине или цилиндре с энерговыделением:
1 - средняя по сечению температура в цилиндре; 2 - средняя по сечению температура в пластине
Эти параметры определялись сравнением экспериментальной кривой изменения температуры на выходе из ТВС с расчетной. Измерения показали существенное увеличение контактного термического сопротивления между топливом и оболочкой твэла при низких температурах на пониженных уровнях мощности. На рис. 26 показаны результаты регистрации температуры на выходе из ТВС реактора БН-600 при быстром снижении мощности с 18 % номинальной с помощью сброса стержня АЗ-П и результаты ее расчета в этих условиях при различных значениях Bi (отношения термического сопротивления топлива к контактному сопротивлению). Наилучшее согласие расчета с экспериментом наблюдается при Bi = 2,1. Для номинальной мощности Bi≈5,7.
Переходные процессы в теплообменных аппаратах, трубопроводах, смесительных камерах. Теплообменные аппараты АЭС с быстрыми реакторами обладают некоторыми конструкционными особенностями, которые сказываются на их динамических характеристиках. Эти аппараты имеют противоточную схему, поскольку она позволяет добиться минимальных температурных разностей между первым и вторым контурами при равных значениях среднелогарифмического температурного напора.
Давление в жидкометаллических контурах невелико. Поэтому теплопередающие трубки и корпуса теплообменных аппаратов имеют сравнительно небольшую толщину и теплоемкость. В связи с этим их влияние на переходной процесс несущественно.
Для исключения в целях безопасности протечек теплоносителя первого контура во второй контур давление в теплообменнике со стороны второго контура принимают более высоким, чем со стороны первого контура. В реакторах типа БН-600 в целях уменьшения перепада уровней натрия между баком реактора и насосом необходимо иметь минимальное гидравлическое сопротивление теплообменника по первому контуру. Вследствие этого теплоноситель первого контура в существующих аппаратах течет в межтрубном пространстве, теплоноситель второго в трубках. При этом объем и полная теплоемкость теплоносителя первого контура в теплообменнике обычно существенно превышает объем и теплоемкость теплоносителя второго контура. Это обстоятельство можно использовать в упрощенных оценках динамических характеристик теплообменных аппаратов.
Расчет переходных процессов в этих аппаратах требует решения уравнений энергии для теплоносителей обоих контуров и нестационарных уравнений теплопроводности для корпусов и теплопередающих трубок. Все эти уравнения представляют собой дифференциальные уравнения в частных производных. Аналитическое решение указанной системы уравнений даже при постоянных расходах теплоносителей не выражается в элементарных функциях. В практических расчетах динамики теплообменников используют численные методы. Поэтому здесь мы ограничимся лишь некоторыми результатами, относящимися к стационарным и переходным режимам их работы. В частности, полезно привести выражения для распределения температуры по длине теплообменников в стационарном режиме:
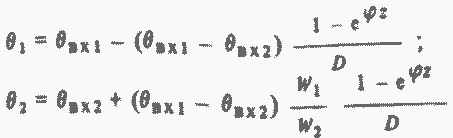
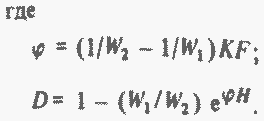
(120)
(121)
(122)
(123)
В этих выражениях θ1, θ2 - температуры теплоносителя первого и второго контуров в произвольном сечении теплообменника; θвх1, θвх2 - те же температуры на входе в теплообменник; W1, W2 - водяные эквиваленты теплоносителей первого и второго контуров (произведения расходов на теплоемкость); К - коэффициент теплопередачи; F — площадь поверхности теплообмена на единицу длины; Н — длина теплообменника; z - осевая координата, отсчитанная от входа по первому контуру.
Средние по длине теплообменника температуры теплоносителей
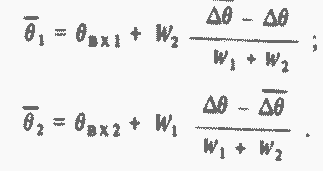
(124)
(125)
Отсюда видно, что при работе на малых уровнях мощности, например в режиме отвода остаточного энерговыделения, когда среднелогарифмический температурный напор в теплообменнике Δ0 значительно меньше разницы входных температур теплоносителей Δθ=θвх1-θвх2, теплообмен в нем происходит на очень небольшом участке со стороны входа теплоносителя с меньшим водяным эквивалентом. Действительно, если W1<W2, то при
Δθ<Δθ θ1≈θ2≈θвх2, т.е. теплоноситель первого контура, войдя в теплообменник, сразу же охлаждается до входной температуры теплоносителя второго контура. При W2<W1, получим θ1≈θ2≈θвх1. Это означает, что теплоноситель второго контура на небольшом входном участке нагревается до входной температуры теплоносителя первого контура. Таким образом, если расход натрия во втором контуре значительно больше расхода в первом, то практически весь промежуточный теплообменник остается ’’холодным”, т.е. имеет такую же температуру, как натрий второго контура на входе. В противном случае весь он разогрет до входной температуры первого контура. Это обстоятельство играет важную роль в режимах естественной циркуляции теплоносителей, поскольку вклад вертикальных промежуточных теплообменников в движущий напор естественной циркуляции значителен.
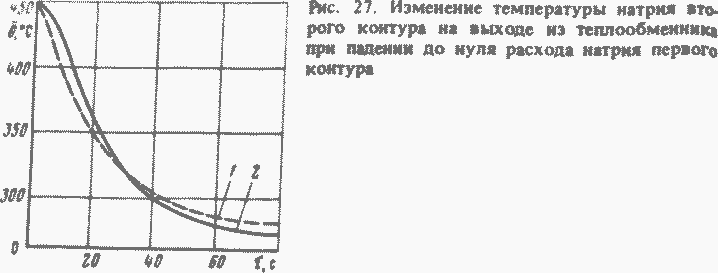
Динамические характеристики теплообменного аппарата, как уже говорилось, могут быть получены в элементарном виде лишь при большом числе упрощений в математическом описании задачи. Если пренебречь теплоемкостью теплопередающих трубок и теплоносителя второго контура, а для теплоносителя первого контура использовать модель с сосредоточенными параметрами, предполагая линейность распределения его температуры по длине, то теплообменный аппарат при таких допущениях превращается в одноемкостное звено. На рис. 27 построены кривые рассматриваемого переходного процесса для теплообменника реактора БН-350. При этом расчетная кривая 1 получена по (131), а кривая 2 - из точного расчета теплообменника на ЭВМ. Согласие между точным и приближенным расчетами удовлетворительное. Из расчета видно, что постоянная времени теплообменника составляет около 30 с. Большие постоянные времени имеют теплообменники и других реакторов. Поэтому они практически не пропускают быстрых изменений температуры на вход реактора.
Решение задачи о динамике теплообмена жидкости, текущей по трубопроводу, с его стенками также довольно громоздко. Поэтому для оценочных расчетов можно предложить лишь приближенные методики.
Если не учитывать теплообмена жидкости со стенками трубы, то температура жидкости на любом удалении от входа повторяет входную температуру с транспортным сдвигом по времени:
![]() (133)
(133)
Если расход теплоносителя через трубопровод изменяется во времени, то транспортный сдвиг т, также оказывается переменным. Поэтому в этих условиях форма температурной кривой в произвольном сечении трубопровода не повторяет входной зависимости. Пусть отклонение от начального значения температуры на входе изменяется во времени по экспоненциальной зависимости![]() , а расход теплоносителя через трубопровод - по гиперболической:
, а расход теплоносителя через трубопровод - по гиперболической:
![]()
При этом отклонение температуры теплоносителя в произвольном сечении трубопровода для т > т*от начального значения:
![]()
где τ0 - транспортное время при расходе G0.
При указанной зависимости расхода от времени
![]() (135)
(135)
Для τ<τ, имеем θ= 0.
В расчетах при низких скоростях изменения температуры иногда используется допущение о равновесном теплообмене в трубопроводе, т.е. о таком теплообмене, когда стенка трубопровода успевает изменять свою температуру вслед за температурой теплоносителя. Это допущение эквивалентно в расчете увеличению транспортного времени пропорционально отношению теплоемкости трубопровода к теплоемкости теплоносителя.
Это явление изучается в расчетах и экспериментах, поскольку оно играет важную роль в формировании поля термических напряжений в элементах внутриреакторных конструкций, оказывает существенное влияние на развитие естественной циркуляции теплоносителя в контурах. Стратификация теплоносителя возможна не только в смесительных камерах, но и в трубопроводах большого диаметра. Эксперименты на действующих установках дают различные результаты. Исследования динамики реактора БН-350 с помощью небольших синусоидальных колебаний мощности показали удовлетворительное перемешивание теплоносителя в его баке. Это показано на рис. 31, где амплитудно-частотные характеристики бака, построенные по формуле (93), соответствующей идеальному перемешиванию теплоносителя, сравниваются с измерениями. В баке реактора БН-600 картина течения натрия более сложная, и допущение об идеальном перемешивании там не оправдывается.

