Расчет переходного процесса в ядерном реакторе сводится к совместному решению уравнений, описывающих изменение его мощности, температурного поля активной зоны, реактивности за счет температурных эффектов, а также за счет работы систем автоматического регулирования, АЗ. Во многих случаях дополнительно к ним потребуется решена уравнений динамики теплообменных аппаратов, ПГ, трубопроводов уравнений нестационарной гидравлики. Здесь не ставится задача подробного и цельного изложения методов расчета переходных процессов ядерно-энергетических установках с быстрыми реакторами. В нижеследующих разделах сделана попытка с привлечением простых математических моделей проиллюстрировать различные стороны физики переходных процессов - нейтронно-физических, тепловых, гидравлических. При этом математические модели и описания процессов выбирались такими чтобы они, несмотря на простоту и наглядность, были пригодны и достаточно точны для количественных экспресс-оценок различных параметров переходных процессов, потребность в которых часто возникает при эксплуатации установок.
Таким образом, в этом случае период реактора, т.е. время изменения мощности в е раз, равен
![]()
Поскольку время жизни мгновенных нейтронов / — величина очень малая, то период реактора при разгоне на мгновенных нейтронах также очень мал даже при небольших превышениях р над β. Регламент эксплуатации, конструкция, система аварийной защиты реактора практически исключают возможность его разгона на мгновенных нейтронах. Поэтому в процессе эксплуатации не возникает необходимости каких-либо оценок подобных переходных процессов. В реальных переходных процессах peaктивность при положительных ее отклонениях всегда значительно меньше эффективной доли запаздывающих нейтронов. В таких процессах скорости изменения мощности сравнительно невелики, поэтому левой часты (1) можно пренебречь и считать ее равной нулю. Это означает, что полагается равным нулю время жизни мгновенных нейтронов. Если дополнительно к этому опишем запаздывающие нейтроны одной группой то получим следующую зависимость мощности реактора от времени поел ступенчатого изменения реактивности:
![]()
где![]() — реактивность, выраженная в долях β. Как видим, в этом случае период реактора составляет
— реактивность, выраженная в долях β. Как видим, в этом случае период реактора составляет
![]()
В общем случае под периодом реактора понимают отношение его мощности к скорости ее изменения:
![]()
Если мощность реактора изменяется во времени не по экспоненциальному, а по любому другому закону, то период не является постоянно величиной. В соответствии с (7) период может быть положительным и отрицательным. В стационарном режиме работы, когда скорость изменения мощности равна нулю, период стремится к бесконечности.
Выражение (5) показывает, что сразу после скачка реактивности мощность мгновенно изменяется и далее растет или падает в зависимости от знака реактивности с периодом, определяемым по (6).
Нужно сказать, что решение (5) в задачах, связанных с повседневно эксплуатацией, имеет ограниченное применение. В эксплуатационной практике гораздо чаще приходится отвечать на вопрос: как нужно изменят реактивность, чтобы обеспечить изменение мощности реактора по заданному закону? В настоящее время большинство реакторов оснащаете реактиметрами.
Эксплуатационный персонал успешно пользуется этими приборами в режимах подъема и снижения мощности. Регламентами эксплуатации реакторов часто предусматриваются режимы подъема мощности с постоянным периодом, подъема и снижения мощности с постоянной скоростью. Может возникнуть необходимость изменения мощности реактора во времени и по другим законам, например кратковременного снижения или повышения ее с последующим восстановлением исходного значения. Во всех этих случаях управление реактором упрощается, если известны необходимые зависимости реактивности от времени, которые соответствуют заданным законам изменения мощности. Получим приближенное решение уравнений кинетики относительно реактивности р(τ) при любой заданной функции п (τ). Поскольку решение предназначено для р < 1, левой частью (1) пренебрегаем, полагая ее равной нулю. При этом (1) можно переписать следующим образом:
![]()
Здесь реактивность, как уже было сделано выше, выражена в долях β;
![]()
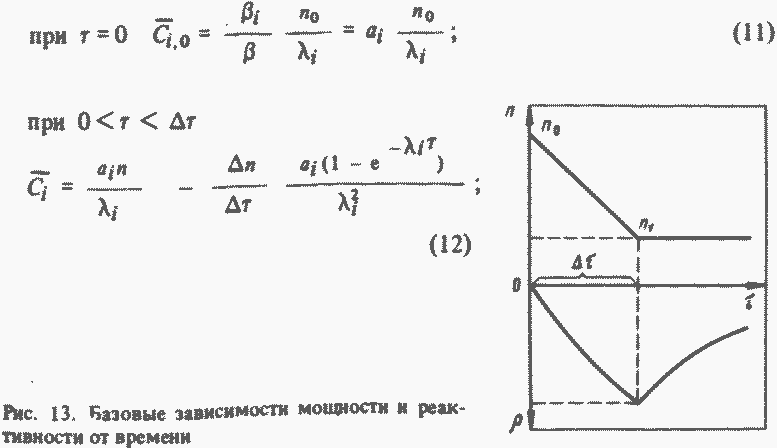
Вначале получим изменение реактивности при подъеме или снижении мощности реактора с постоянной скоростью за время Δτ на заданную величину с последующим поддержанием ее на постоянном уровне (рис. 13):

Для такого изменения мощности из решения уравнения (2) получим следующие выражения для концентрации ядер-предшественников запаздывающих нейтронов ьй группы:
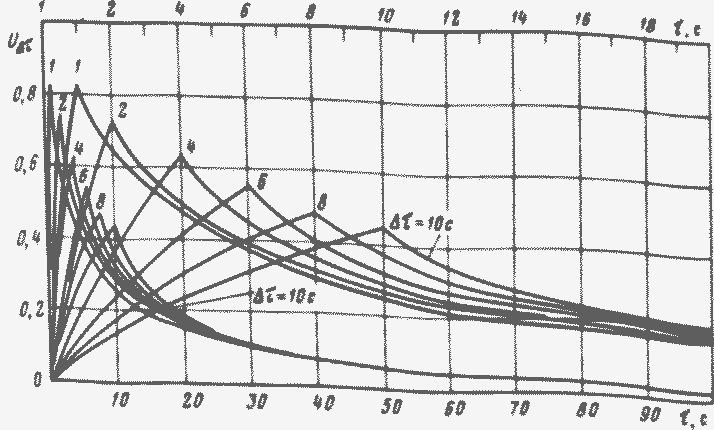
с. 14. Функции линейного отклика для урана:
нижняя шкала времени относится к нижней группе кривых, верхняя к верхней
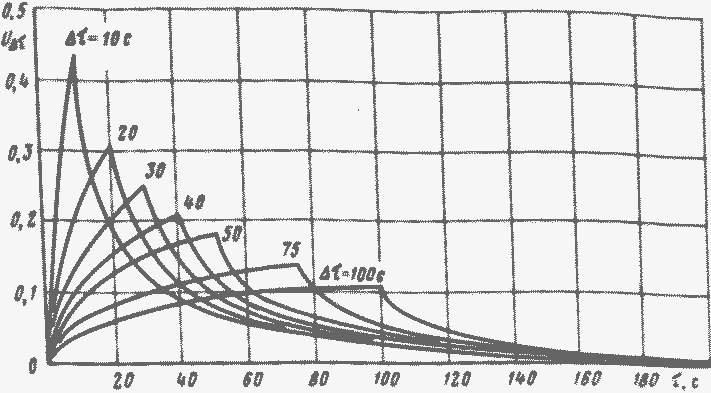
Рис. 15. Функции линейного отклика для урана; цифры у кривых - значения Δτ, с
Функции линейного отклика UΔт(т) для различных Δτ построены на рис. 14 и 15 для реактора, основным делящимся нуклидом в котором является уран-235. В приложении даны табличные значения этих функций как для урана, так и для плутония. Их использование очень упрощает расчет законов изменения реактивности.
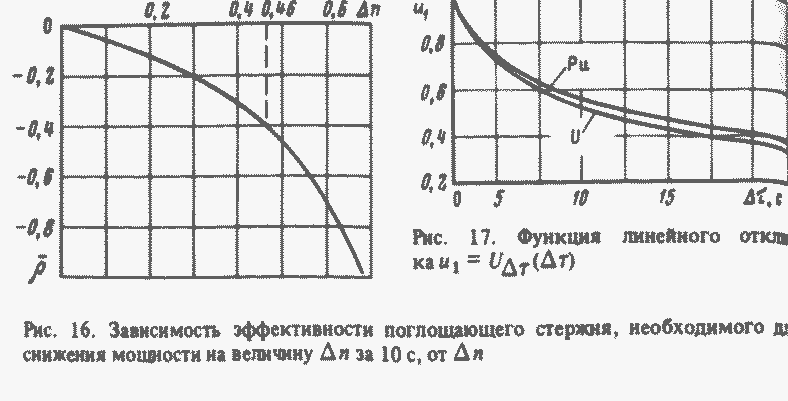
Для примера на рис. 16 представлены рассчитанные с помощью этих функций изменения реактивности, необходимые для различных снижений мощности реактора за 10 с. Это время близко к минимальному времени полного хода стержня автоматического регулятора реактора БН-600. Эффективность одного поглощающего стержня составляет около 0,4 β. Расчет показывает, что за счет ввода такой отрицательной реактивности за 10 с мощность реактора может быть снижена на 46 % исходного значения.
Нужно, конечно, учитывать, что если исходная мощность реактор велика, то в процессе ее снижения появятся температурные эффекты реактивности, которые уменьшат абсолютное значение фактически введенной реактивности за время полного хода PC. Поэтому приведенная выше количественная оценка справедлива для достаточно низкого исходного уровня мощности, на котором температурные эффекты не играют большой роли. Температурные эффекты и другие факторы, влияющие на реактивность, будут рассмотрены ниже. В решении же уравнений кинетики реактивность выступает как интегральный параметр, представляющий собой результат совокупного действия всех этих факторов. В качестве такого параметра реактивность контролируется реактиметром.
Из (14) получим следующее значение конечного уровня мощности реактора n1, которое достигается после ввода реактивности р за время Δτ:
л1=ло/1 - I (19
/ L С/Дт(Дт) J
Из (5) также получим значение уровня мощности n1, которое достигается сразу же после мгновенного ввода реактивности: n1=n0/(1-р).
Это выражение часто используется для оценок отклонений мощности и только при мгновенных, а и при достаточно быстрых изменениях peaктивности, когда концентрации ядер-предшественников запаздывающие нейронов фактически остаются постоянными. Это справедливо, если время изменения мощности значительно меньше среднего времени жизни запаздывающих нейтронов. Сравнение (19) и (20) показывает, что функция UΔτ учитывает изменение вклада запаздывающих нейтронов за врем снижения мощности. Функция UΔτ(Δτ) изображена на рис. 17. Он представляет собой кривую, проведенную по максимумам кривых UΔτ(τ)представленных на рис. 14 и 15.
Эта кривая показывает, что изменении вклада запаздывающих нейтронов довольно существенно даже в тех случаях, когда мощность изменяется за несколько секунд. Например, для Δτ=10 с u1=UΔτ(Δτ)=0,465. Если Δτ=1 с, то u1=0,834. Поэтому даже при Δτ = 1 с оценка отклонений мощности по (20) будет иметь существенную погрешность. Такой оценкой, например, пользуются при определении мощности реактора, которая достигается сразу же после падения в его активную зону стержней АЗ. Время падения стержней составляет 0,8-1 с. Предпочтительнее и здесь пользоваться выражением (19), которое не дает указанной погрешности.

