§ 35. Вычисление максимальных расходов половодья при отсутствии наблюдений
Вычисление величин максимальных расходов половодья при недостатке наблюдений оказывается затруднительным ввиду отсутствия единой достаточно обоснованной методики расчета. Для вычисления максимальных расходов при отсутствии наблюдений имеется ряд эмпирических формул, полученных для различных географических районов.
Некоторые формулы, имеющие простой вид, в обобщенном виде учитывают влияние отдельных факторов, определяющих величину максимальных расходов. Эти суммарные влияния ряда условий формирования максимумов оцениваются введением обычно одного эмпирического коэффициента.
Существуют также формулы более сложного вида, содержащие ряд эмпирических коэффициентов, которые более дифференцированно оценивают условия образования максимальных расходов.
Однако в этих формулах большое число коэффициентов определяется эмпирическим путем, что создает значительные трудности и в результате желаемого уточнения не достигается из-за ошибок в определении коэффициентов.
Вообще же точность результатов вычислений по той или иной формуле зависит от того, насколько близко гидрологические условия в расчетном створе отражены в исходных материалах, положенных в основу составления формулы. Следует иметь в виду, что большинство эмпирических формул получено по материалам наблюдений на крупных реках, поэтому при расчетах сельских ГЭС для контроля желательно производить оценку применимости расчетных формул для рассматриваемого бассейна. Для этого можно рекомендовать проверку формул на ближайших реках-аналогах с длительными рядами наблюдений и далее вести расчет методом аналогии, используя формулу, дающую лучшие результаты.
Ниже приводятся наиболее употребительные эмпирические формулы из числа имеющихся для вычисления максимальных расходов половодья при отсутствии наблюдений.
1. Формула Д. Л. Соколовского. Д. Л. Соколовским в результате обработки обширных материалов по максимальным расходам половодий получена формула следующего вида:

Наибольшие максимумы половодья обычно имеют место после суровой зимы при мерзлой земле и коэффициент стока α в этом случае близок к его предельному значению, равному единице.
При этом максимальная интенсивность элементарного стока будет численно равна максимальной интенсивности снеготаяния, т. е.

Однако карты изолиний и параметра А не учитывают частных особенностей и всего разнообразия физико-географических условий отдельных водосборов и могут служить лишь для приближенной оценки величин максимальных расходов.
Поэтому основным методом для определения параметра А является метод гидрологической аналогии.
Для выбора подходящего аналога необходимо прежде всего тщательно изучить материалы, относящиеся к изучаемому бассейну и к бассейнам, намечаемым в качестве аналогов.
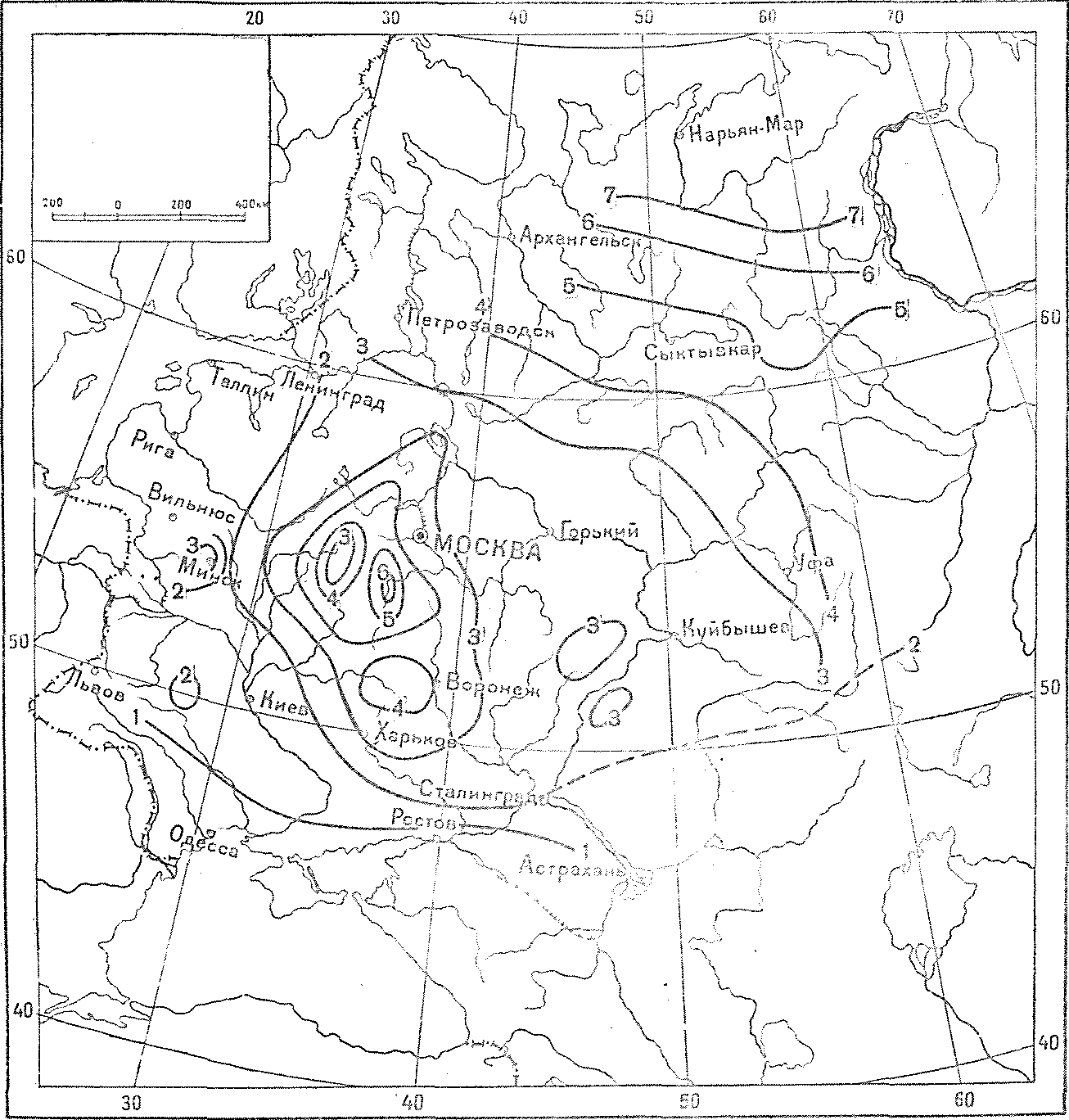
Рис. 57. Карта изолиний средних значений параметра А максимального весеннего стока (в мм/час).
К числу таких материалов относятся ведомости измеренных расходов, гипсометрические карты бассейнов, карты распределения снежного покрова, данные о сроках наступления и продолжительности половодья, данные о лесистости, озерности и заболоченности бассейнов, а также сводные таблицы параметра А для рассматриваемого района и сведения о стоке в пунктах, не учтенных в сводных таблицах параметра А.

Рис. 58. Карта изолиний коэффициента вариации С максимальных расходов талых вод.
Величины параметра А, полученные для однородного в физико- географическом отношении района, уточняются для расчетного створа с учетом следующих условий:
а) при резко расчлененном рельефе аналог следует выбирать из рек, протекающих на одном склоне с изучаемой рекой;
б) величины лесистости, озерности и заболоченности бассейнов, аналога и изучаемого, должны быть близкими. При заметном расхождении в расчете следует учитывать коэффициенты δ и δ';
в) значительное расширение поймы вызывает распластывание паводка и снижение величины А. Поэтому при выборе аналога следует учитывать морфометрические характеристики русла сравниваемых рек;
г) длительность ряда наблюдений на реке-аналоге должна быть не менее 10—15 лет для надежного вычисления параметра А;
д) площади сравниваемых бассейнов должны быть близкими по величине, так как для малых водосборов принятие постоянного значения η = 0,25 приводит к увеличению модулей стока по сравнению с большими бассейнами, находящимися в тех же условиях.
Выбрав подходящий аналог с учетом указанных условий, по материалам наблюдений определяют для него величины максимальных расходов воды различной обеспеченности. Далее, используя формулу (99), находят величины параметра А заданной обеспеченности.
Затем по. формуле (99) по найденным значениям параметра А вычисляют максимальные расходы искомой обеспеченности для расчетного створа. При различии в озерности, заболоченности или лесистости аналога и рассматриваемой реки вводится поправка в результат расчета.
Рассмотрим пример вычисления максимальных расходов половодья р. Сабы (приток р. Луги) для створа у д. Николаевское с использованием формулы Д. Л. Соколовского и карт изолиний параметров А и CL.





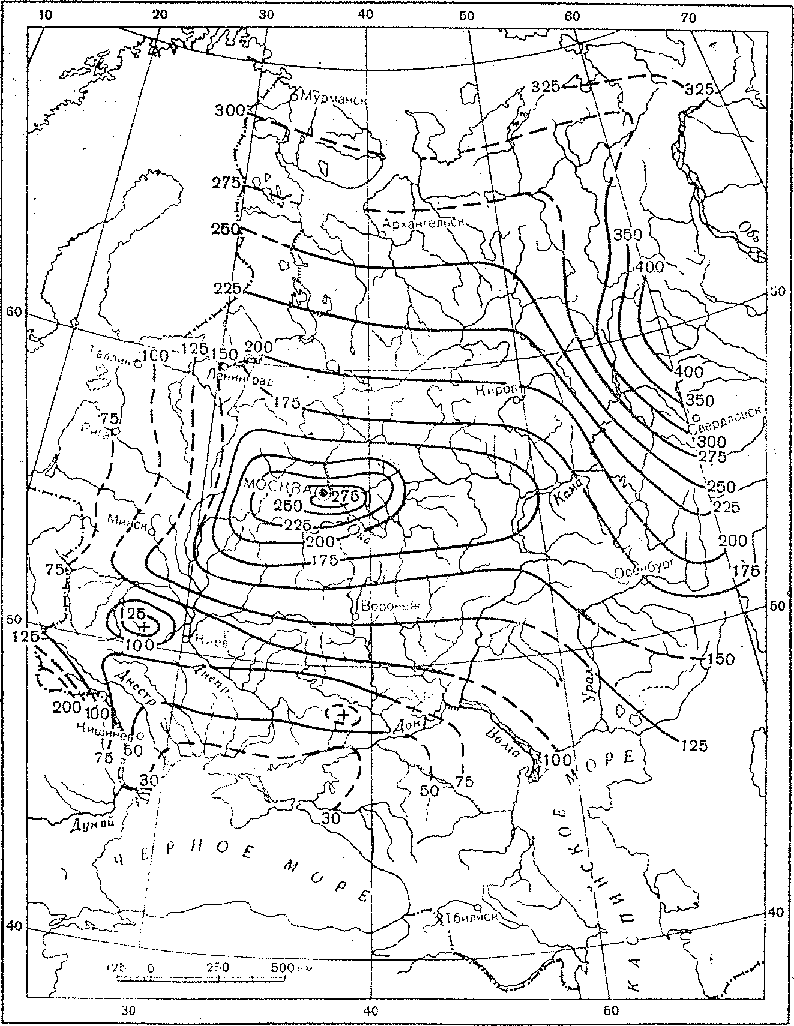
Рис. 59. Карта изолиний суммарного весеннего стока А мм за годы с выдающимися половодьями.

Рис. 60. Карта изолиний продолжительности водоотдачи.



заболоченная. Исходя из этого, принимаем значение коэффициента Кх = 0,80. Поскольку в бассейне имеется 6 озер и болот, регулирующих сток выше расчетного створа, для определения коэффициента зарегулирования максимального расхода τ используем формулу (114).
Таблица 82
Значения переходного коэффициента λ
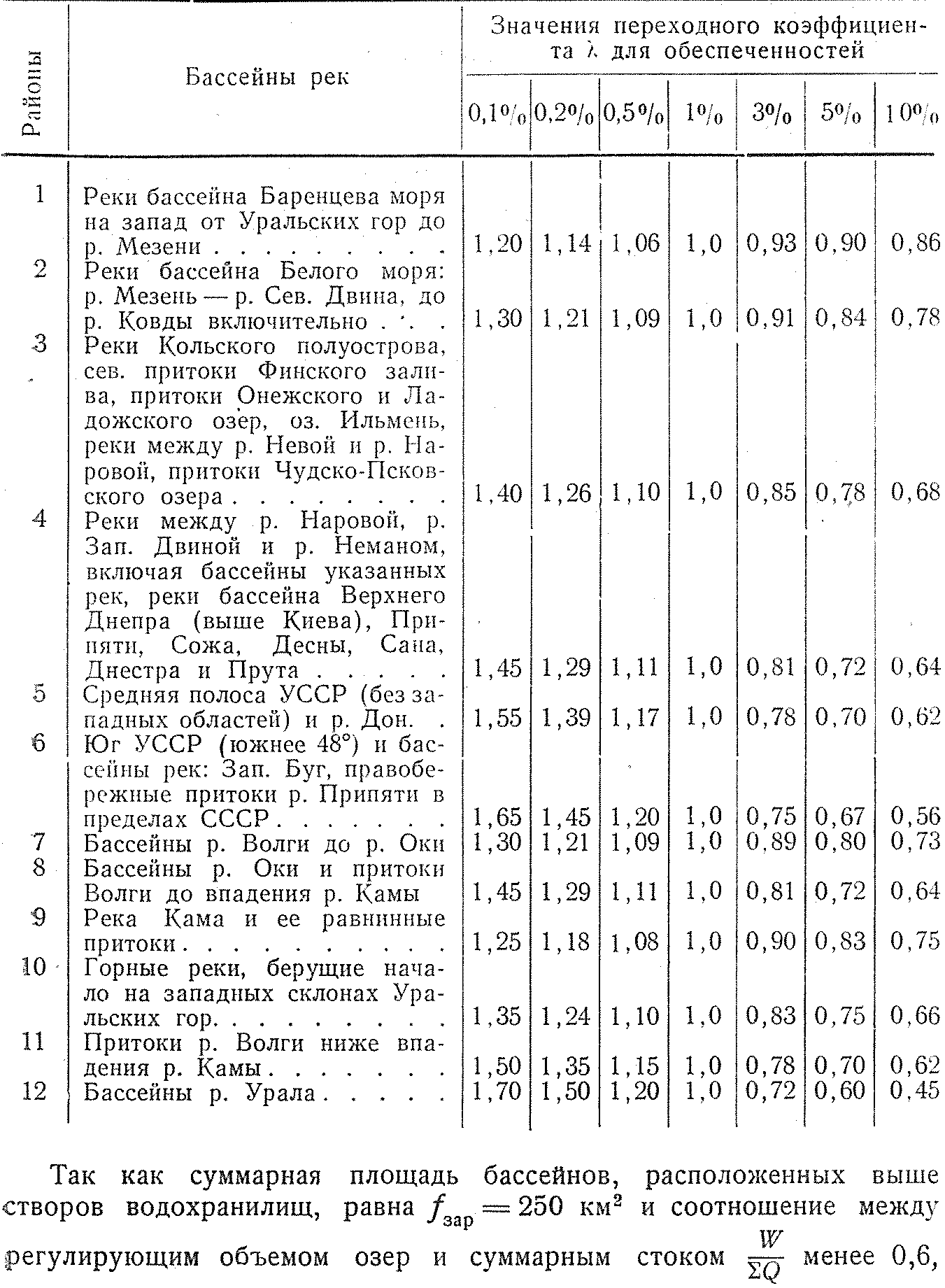


Рис. 62. Карта изолиний среднего многолетнего стока половодий А мм.
учитывающий неодновременность снеготаяния на крупных бассейнах; f1 — коэффициент лесистости; f2 — коэффициент заболоченности бассейна.
Значения параметров А и В определяются по картам изолиний (рис. 62 и 63).
Для вычисления коэффициента С определяют по карте изолиний (рис. 64) средневзвешенную для всего бассейна дату перехода температуры воздуха через 0° — и дату перехода температуры воздуха через 0° в расчетном створе — t2. В зависимости от разности этих дат Δt=t1—t2 величина коэффициента С принимается следующей:

Рис. 63. Карта геоморфологического параметра В в формуле (113).


Рис. 64. Средние многолетние даты весеннего перехода температуры воздуха через 0°.








