§ 25. Построение теоретической кривой, обеспеченности при наличии наблюдений
Как указывалось выше, кривая обеспеченности может быть построена, если известны ее параметры: среднее арифметическое значение ряда х, коэффициент вариации Сv, и коэффициент асимметрии Cs. Для нахождения этих параметров используются результаты наблюдений за гидрологическими величинами.
С этой целью наблюденные величины, например средние годовые расходы, располагаются в расчетной таблице в порядке их убывания.
Вначале суммированием величин расходов за весь период наблюдения и последующим делением результата на число лет наблюдений находится средний многолетний расход. Затем последовательным делением всех средних годовых расходов на величину среднего многолетнего расхода за период наблюдений определяются модульные коэффициенты среднего годового стока для каждого года. Далее в расчетной таблице записываются значения (К—1). и (K—1)2 для каждого года. Эти данные используются для вычисления коэффициента вариации Cv. В этой же таблице вычисляется обеспеченность средних годовых расходов каждого года по эмпирической формуле (44).
При вычислении модульных коэффициентов К общая сумма их значений должна быть равна числу членов ряда n, а сумма (К—1) должна быть равна нулю. Это следует иметь в виду при контроле результатов вычислений.
Для иллюстрации изложенного рассмотрим пример вычисления параметров кривой обеспеченности средних годовых расходов р. Ловать у г. Холм по ряду наблюдений длительностью 26 лет (табл. 40).
Таблица 40
Вычисление параметров кривой обеспеченности средних годовых расходов р. Ловать у г. Холм
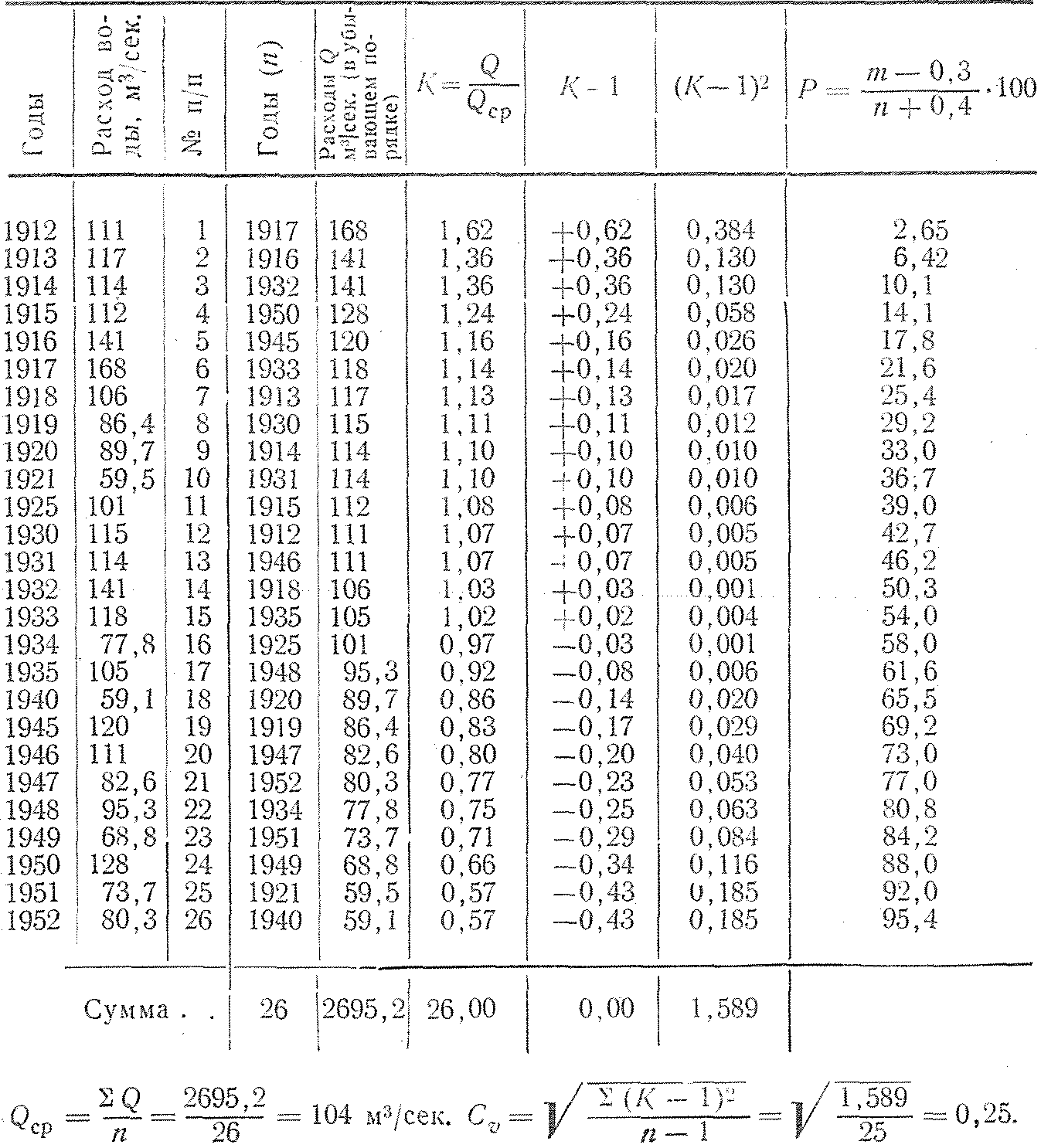
Так как ряд наблюдений недостаточен для вычисления коэффициента асимметрии с необходимой точностью, то значение его принимаем по соотношению Cs=2Cv, откуда Cs=0,50. Определив параметры кривой обеспеченности, можно найти ординаты кривой при различных значениях обеспеченности.
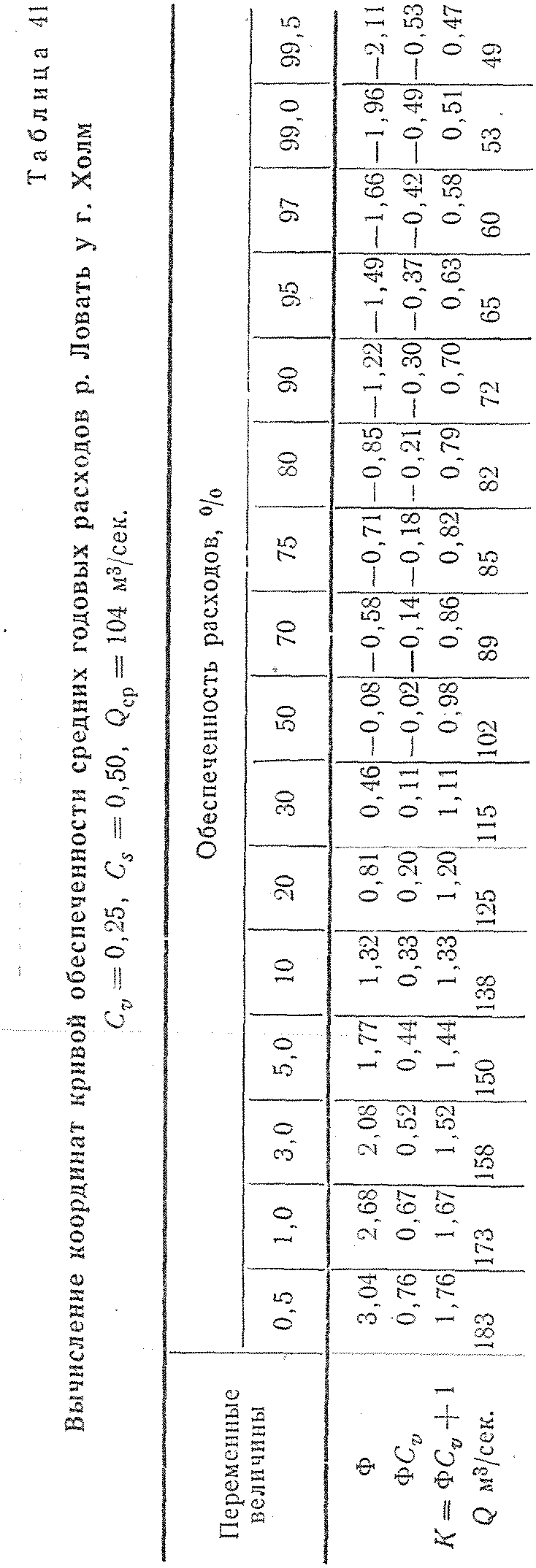
Поскольку биномиальная кривая аналитически выражается некоторым уравнением, рядом исследователей произведено интегрирование этого уравнения и результаты представлены в виде таблиц ординат кривой в зависимости от ее параметров. Наиболее употребительной является таблица С. И. Рыбкина (приложение 3), в которой ординаты кривой обеспеченности даны в виде относительных отклонений от середины при значениях Cv = 1 и Cs — от 0 до 2,0.
Поскольку в расчетах часто применяют значение Cs=2Cv, в приложении 4 дана таблица ординат кривой обеспеченности в зависимости от величины коэффициента вариации Cv.
Для перехода от табличных значений отклонения ординат к их значениям при вычисленной величине Сv, необходимо умножить табличные значения нормированных отклонений ординат Ф (при данном Сs) на величину Сv.

Полученные результаты используются для построения теоретической кривой обеспеченности средних годовых расходов (рис. 29).
Для контроля вычислений и построения теоретической кривой обеспеченности на график наносятся точки, вычисленные по эмпирическим данным по формуле (44) (табл. 40). Такой контроль необходим вследствие тога, что коэффициент асимметрии Cs обычно определяется со значительной погрешностью.
В приведенном примере теоретическая кривая обеспеченности достаточно близко отражает фактическое распределение расходов разной обеспеченности, полученное по материалам наблюдений.
В том случае, когда обнаруживается хорошее совпадение теоретической и эмпирической кривых обеспеченности в средней их части и большое расхождение в зоне малых и больших величин обеспеченности, что свидетельствует о недостаточной точности принятого значения коэффициента асимметрии Cs, поступают следующим образом.
Построив на графике эмпирическую кривую обеспеченности, вычисляют координаты точек теоретических кривых обеспеченности при полученном Cv и при различных значениях Cs и наносят их на тот же график.
Увеличение значения Cs влечет повышение левой части кривой обеспеченности (в зоне малой обеспеченности) и понижение правой части (в зоне высокой обеспеченности). Уменьшение Cs вызывает обратную картину.
Таким образом, задавшись вначале соотношением, например, CS=2CV, производят построение эмпирической и теоретической кривых обеспеченности и их анализируют. При недостаточном совпадении кривых задаются другим соотношением Cv и Cs и полученную кривую также совмещают с эмпирической.
Наиболее близко совпадающая с эмпирической теоретическая кривая обеспеченности используется в дальнейших расчетах и соответствующее ей значение Cs принимается за расчетное. Удовлетворительное совпадение кривых удается получить обычно за две-три попытки. Изложенный способ может дать приемлемый результат лишь в том случае, когда рассматриваемый ряд включает члены с достаточно большими и малыми крайними значениями, т. е. если наряду со средневодными годами в ряду имеются маловодные и многоводные годы.
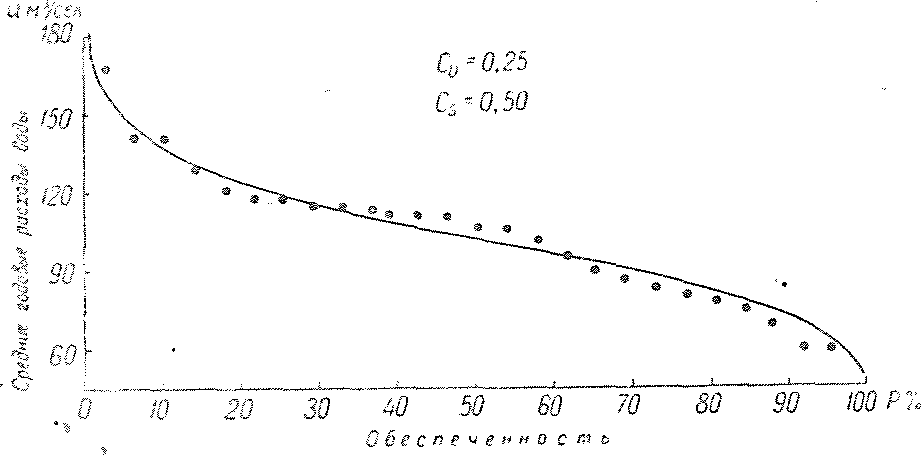
Рис/ 29. Кривая обеспеченности средних годовых расходов воды р. Ловать у г. Холм.
Теоретическая кривая обеспеченности позволяет находить величину расходов любой заданной обеспеченности, непосредственно не измеренных при гидрологических наблюдениях.
Так, например, в рассмотренном примере расход обеспеченностью 50%, т. е. с вероятностью повторения 1 раз в 1,44 года, равен 102 м8/сек.; расход обеспеченностью 99% равен 53 м3/сек. и т. д.
При производстве гидрологических расчетов следует иметь в виду, что расход заданной обеспеченности, например 5%, может иметь среднюю повторяемость 1 раз в 19,5 лет лишь при очень длительном ряде наблюдений и не обязательно должен наблюдаться через каждые 19,5 лет или только один раз в 19,5 лет.
§ 26. Вычисление коэффициента вариации годового стока при удлиненном ряде наблюдений
При коротком периоде наблюдений и при наличии удовлетворительного аналога многолетние колебания годового стока могут быть выявлены путем приведения короткого ряда к длинному с использованием графика связи средних годовых расходов сравниваемых пунктов.
В этом случае коэффициент вариации удлиненного ряда определяется по формуле




