Глава VIII
МАКСИМАЛЬНЫЕ И МИНИМАЛЬНЫЕ РАСХОДЫ ВОДЫ
Определение величин максимальных расходов воды в гидрологических расчетах гидроэлектростанций занимает весьма важное место. Если расчеты годовых колебаний и внутригодового распределения стока необходимы главным образом для установления энергетических параметров ГЭС, то величины максимальных расходов требуются для определения основных размеров подпорных и водосбросных сооружений, являющихся наиболее дорогими элементами в комплексе гидроэнергетического узла. Недостаточно обоснованное завышение расчетных величин максимальных расходов влечет увеличение высоты подпорных сооружений, размеров отверстий водосбросных сооружений, длины проезжих и служебных мостов, числа и мощности подъемных механизмов и пр. Все это вызывает увеличение капитальных затрат на строительство гидростанции и эксплуатационных расходов по ее обслуживанию и в целом снижает экономическую эффективность ГЭС.
Наоборот, занижение расчетных величин расходов против требуемых вызывает опасность возможных повреждений или даже разрушений сооружений при пропуске расходов, превышающих расчетные.
Таким образом, для получения оптимальных размеров сооружений величины максимальных расчетных расходов должны быть определены по возможности наиболее точно в соответствии с принятой их расчетной обеспеченностью.
В „Нормах и Технических Указаниях" („Н и ТУ“) по расчету максимальных расходов воды при проектировании гидротехнических сооружений, разработанных взамен ГОСТ-3999-48, предусматриваются следующие расчетные величины вероятности (в процентах) ежегодного превышения наибольших расходов воды, пропуск которых должен быть обеспечен при нормальных и чрезвычайных условиях эксплуатации (табл. 72).
Таблица 72
За основной расчетный случай принимается работа сооружений при нормальных условиях эксплуатации. Расчет на чрезвычайные условия эксплуатации является поверочным. Во втором случае расчет сооружений производится с возможностью временного превышения нормального подпорного горизонта и нарушения нормальных эксплуатационных режимов работы ГЭС, но при условии сохранности основных сооружений.
При вычислении величин максимальных расходов находят отдельно максимумы, образуемые весенним половодьем, и максимумы дождевых или ливневых паводков. В качестве расчетной величины выбирается наибольшая из этих двух.
§ 34. Вычисление максимальных расходов воды при наличии материалов наблюдений
Задача расчета максимальных расходов половодья или ливневых паводков сводится к определению их величин, соответствующих заданным значениям обеспеченности. При наличии материалов длительных гидрологических наблюдений вычисление величин максимальных расходов заданной обеспеченности не представляет затруднений. По имеющимся данным определяются параметры кривой обеспеченности и строятся эмпирическая и теоретические кривые обеспеченности.
По ряду максимальных расходов за годы наблюдений находится средний максимальный расход как среднее арифметическое ряда годовых максимальных расходов Q
(84).
Коэффициент вариации максимальных расходов определяется по формуле:
По „Н и ТУ“ для расчетов максимальных расходов воды при вычислении коэффициента асимметрии максимумов дождевых паводков равнинных рек может применяться соотношение
основанное на опыте проектирования по рекам Европейской территории СССР, водосборы которых расположены в зоне достаточного увлажнения. Большие значения Cs должны применяться при расчете максимальных расходов воды рек, водосборы которых сравнительно невелики и расположены в областях с менее влажным климатом.
По найденным параметрам теоретическая кривая обеспеченности максимальных расходов строится в соответствии с изложенной выше методикой вычисления и построения кривых обеспеченности.
Ввиду возможного преуменьшения расчетных величин максимумов, что может иметь место, если рассматриваемый период наблюдений не отражает в достаточной мере характер колебания стока, согласно „Н и ТУ“, вычисленные величины максимальных расходов увеличиваются прибавлением так называемой гарантийной поправки.
Принято считать, что результаты расчетов по ряду наблюдений являются достаточно надежными, если при длительности ряда не менее 20 лет гарантийная поправка составляет не более 20% от величины максимального расхода, найденного по кривой обеспеченности.
Гарантийная поправка добавляется к величинам максимальных расходов, определяемых только для случаев расчета на чрезвычайные условия эксплуатации.
К величинам максимальных расходов, вычисленных для условий нормальной эксплуатации, гарантийная поправка не прибавляется.. Для вычисления величины гарантийной поправки используется следующая формула С. Н. Крицкого и Μ. Ф. Менкеля:
(85)
где ΔQ — величина гарантийной поправки к расходу Qp; а — коэффициент, принимаемый равным от 0,7 до 1,5 в зависимости от степени гидрологической изученности реки (для рек, достаточно изученных, а=0,7; для рек, недостаточно изученных, для которых вычисленные величины максимальных расходов из-за недостатка данных не могут быть проконтролированы по результатам расчетов для аналогов, а также в случае, если кривая зависимости расходов воды от уровней является ненадежной, а = 1,5); N — число лет наблюдений;. Qp— расход заданной обеспеченности Р, определяемый по кривой обеспеченности для случая чрезвычайных условий эксплуатации; Ер — относительная средняя квадратичная ошибка ординаты кривой обеспеченности, определяемая по графику (рис. 54).
„Нормами и Техническими Указаниями" гарантийную поправку рекомендуется вводить при расчете отверстий водосбросных сооружений только первых двух классов капитальности на чрезвычайные условия эксплуатации гидроузла.
На графике теоретической и эмпирической кривых обеспеченности строится в пределах малых обеспеченностей кривая обеспеченности с гарантийной поправкой.
Последняя кривая должна лежать выше первых двух.
Если отдельные точки эмпирической кривой обеспеченности располагаются выше кривой с гарантийной поправкой, то следует произвести анализ кривых, установить причину этого отклонения и вновь построить теоретическую кривую обеспеченности, изменив величину коэффициента асимметрии.
Если при изысканиях в результате опроса старожилов по меткам высоких вод или по историческим архивным данным имеется возможность установить хотя бы приближенно величину наибольшего максимального расхода за период N лет, превышающий период наблюдений п лет, то эти данные могут быть использованы для уточнения средней многолетней величины максимального расхода Qcp чакс и коэффициента вариации Cv кривой обеспеченности.
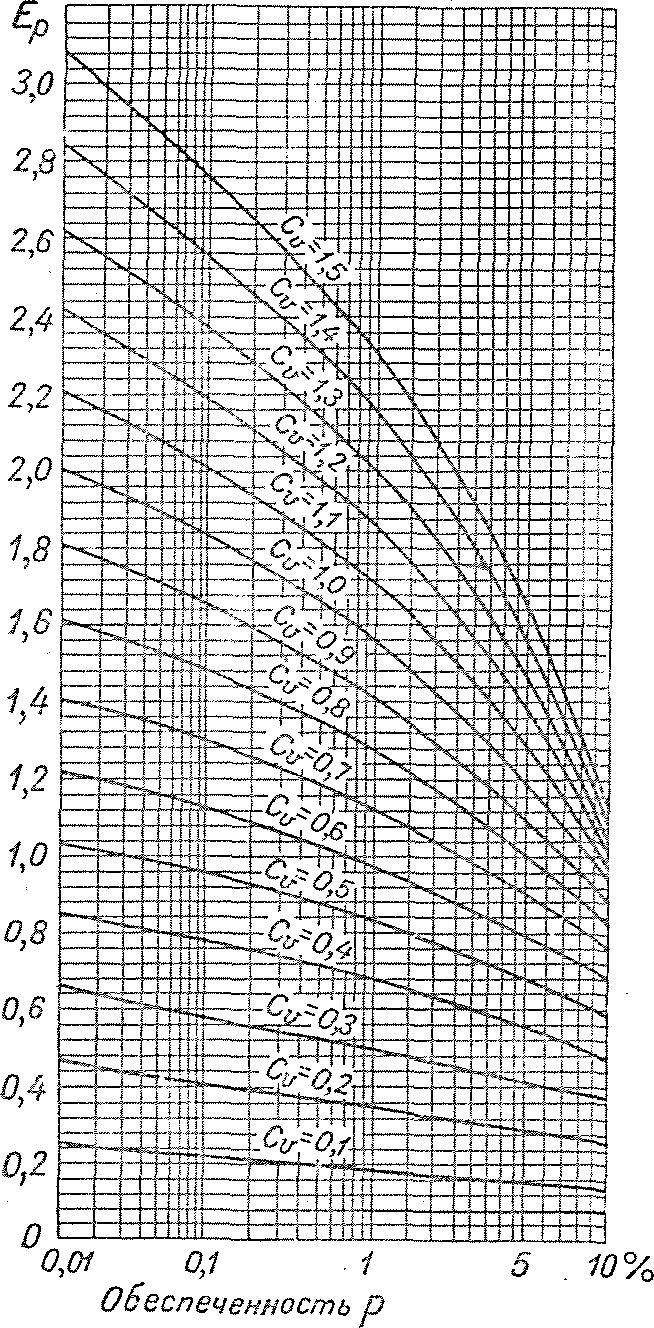
Рис. 54. График для определения величины Ер.
Для этого можно воспользоваться формулами С. Н. Крицкого и Μ. Ф. Менкеля, имеющими следующий вид: где QN — величина выдающегося максимального расхода за период N лет; п — число лет наблюдений за стоком.
Вычислив по формулам (86) и (87) уточненные величины Qcp макс и Cv, находят ординаты кривой обеспеченности, которую используют для расчета, с введением в необходимых случаях гарантийной поправки.
Рассмотрим изложенный порядок вычисления максимальных расходов при наличии материалов наблюдений на примере расчета для р. Шелони у д. Заполье.
Вычисление коэффициента вариации максимальных расходов по наблюдениям за 26 лет приведено в табл. 73, в которой указаны также обеспеченности расходов, найденные по эмпирической формуле.
Таблица 73
Вычисление коэффициента вариации максимальных расходов воды половодья р. Шелони у д. Заполье
В 1922 г. на р. Шелони наблюдался исключительно высокий паводок, максимальный расход которого, установленный гидравлическим способом и по экстраполяции кривой зависимости расходов воды от уровней оказался равным QN=2200 м3/сек.
В результате изысканий удалось установить, что местные старожилы не наблюдали уровня воды р. Шелони, подобного максимуму 1922 г., и им не было известно от прежних поколений о столь высоких уровнях р. Шелони.
Паводок 1922 г. был катастрофическим не только в бассейне р. Шелони, но и в соседних бассейнах рек Черехи, Полисти, Сороти. Так, в дер. Костыжицы на р. Шелони было подтоплено здание церкви, построенной в конце XVIII в.; в дер. Виделетье на р. Черехе была подтоплена церковь, построенная в XIV в.
В результате паводка 1922 г. целые деревни были смыты водой. Много домов и деревянных построек было снесено в оз. Ильмень. Многие мельничные и другие постройки, имевшие давность свыше 100—150 лет, были уничтожены или затоплены водой. Паводок наступил через 5—6 дней после очищения реки от льда и не был заторным.
Все это указывает на то, что паводок 1922 г. был очень редкой повторяемости, по-видимому, не менее 1 раза в 200 лет.
Используя формулы (86) и (87), вычислим средний многолетний максимальный расход половодья Qcp макс и коэффициент вариации Cv для случаев повторяемости максимума паводка 1922 г. 1 раз в 200, 300, 500 лет. При повторяемости указанного максимума 1 раз в 200 лет:
Таблица 74
Средние максимальные расходы половодья р. Шелони у д. Заполье в зависимости от повторяемости паводка 1922 г.
Рис. 55. Кривые обеспеченности максимальных расходов половодья р. Шелони у д. Заполье.
Как видно из графика, кривая обеспеченности при
лучше соответствует эмпирическим точкам, чем при
, поэтому она принимается за расчетную.
Здесь же построена часть кривой обеспеченности с гарантийной поправкой, величина которой вычислялась по формуле (85).
Результаты вычисления гарантийной поправки и расчетные величины максимальных расходов р. Шелони у д. Заполье приведены в табл. 75.
Наибольшая величина гарантийной поправки в рассмотренном примере оказалась меньше 20% от величины максимального расхода; длительность ряда наблюдений (26 лет) превышает продолжительность периода наблюдений, требуемую по „Н и ТУ“ для получения надежных результатов (20 лет), поэтому результаты произведенного расчета можно считать приемлемыми.
Если ряд наблюдений за максимальными расходами невелик, но имеется хороший аналог для рассматриваемой реки с длительными наблюдениями, то следует произвести удлинение ряда для расчетного створа. Для этого строится график связи максимальных расходов в расчетном створе и в створе реки-аналога, по которому определяются величины максимальных расходов половодья за годы недостающих наблюдений. Построение и использование графика связи максимальных расходов такое же, как и для графика уровней воды среднегодовых расходов и др. По полученному удлиненному ряду определяются параметры кривой обеспеченности максимальных расходов половодья и производится ее построение так же, как и при наличии продолжительных наблюдений.
Таблица 75
Максимальные расходы половодья р. Шелони у д. Заполье
Наряду с построением кривой обеспеченности максимальных расходов по удлиненному ряду нахождение расчетного максимального расхода целесообразно производить непосредственно по кривой связи максимумов, определяя его как расход, соответствующий расходу заданной обеспеченности реки-аналога. Результаты определения максимального расхода обоими способами сравниваются между собой и в случае значительного расхождения производится анализ построенных кривых и их отдельных точек и вносятся необходимые коррективы.
Если надежного аналога не имеется и удовлетворительной связи максимальных расходов получить не удается, построение кривой обеспеченности производят по результатам короткого ряда наблюдений, хотя точность расчета при этом и понижается.
Длительность ряда, используемого для построения кривой обеспеченности, должна быть не менее 15 лет, при условии, что ряд также включает 1—2 многоводных года.
Если удлинение ряда по данным аналога произвести не представляется возможным, а число лет наблюдений в расчетном створе мало, расчет максимальных расходов производится так же, как и при отсутствии наблюдений.
где Кмин— отношение наинизшего из наблюденных максимальных расходов к среднему.
Эта формула дает удовлетворительные результаты в том случае, если точка наименьшего максимального расхода лежит на эмпирической кривой или близко от нее. В противном случае возможна большая ошибка.
Формула М. В. Мялковского для вычисления коэффициента асимметрии имеет следующий вид:
(94)
В этом случае повторяемость расходов определяется следующим образом. При общем числе паводков т за п лет наблюдений средняя повторяемость паводков в год равна
Вычисление максимальных расходов дождевых паводков при наличии наблюдений производится аналогично вычислению максимальных расходов весеннего половодья. На реках, на которых в течение года наблюдается несколько дождевых паводков, в ряд расчетных величин включаются не только годовые максимумы, но и все максимальные расходы паводков, равные самому низкому годовому максимуму из числа наблюденных и превышающие его. Таким образом, расчетный ряд максимальных расходов иногда превышает число лет наблюдений.
Следует иметь в виду, что указанные формулы для перехода от обеспеченности дождевых максимумов Р% к их повторяемости 1 раз в N лет можно применять при N>10 лет или при Р<10%. При других значениях N и Р следует пользоваться формулой (41).
Большинство равнинных рек Европейской территории СССР характеризуется высоким половодьем, низкой летней и зимней меженью и повышенным стоком осенью. Дождевые паводки обычно бывают не чаще одного раза в год в осенний период с максимумами ниже максимумов половодья.
Паводки с высокими максимумами наблюдаются сравнительно редко, поэтому для определения расчетных величин максимальных расходов малой обеспеченности необходимо располагать длительным рядом наблюдений, включающим выдающиеся максимумы. Поскольку таких данных при расчетах сельских ГЭС, как правило, не имеется, следует значительное внимание уделять сбору сведений о выдающихся максимумах в процессе изысканий. По меткам высоких вод на местности, по опросам старожилов и архивным данным устанавливаются уровни и уклоны водной поверхности в паводок. По этим материалам гидравлическим расчетом определяется величина паводкового расхода воды, соответствующая установленным отметкам уровня.
Таблица 76
Вычисление коэффициента вариации максимальных расходов дождевых паводков р. Шелони у д. Заполье
В табл. 76 приведены расчетные данные для вычисления ординат теоретической кривой обеспеченности максимальных расходов дождевых паводков на р. Шелони у д. Заполье; на рис. 56 представлена эта кривая.
Рис. 56. Кривая обеспеченности максимальных расходов дождевых паводков на р. Шелони у д. Заполье.
Из сравнения кривых обеспеченности максимальных расходов весеннего половодья (рис. 55) и дождевых паводков для р. Шелони видно, что максимумы весеннего половодья превосходят по величине
максимумы дождевых паводков такой же повторяемости. Коэффициент вариации максимальных расходов дождевых паводков более чем в два раза превышает коэффициент вариации максимумов половодья. Эмпирическим точкам кривой обеспеченности максимумов дождевых паводков наиболее соответствует теоретическая кривая обеспеченности с коэффициентом асимметрии Cs=2Cv, которая и принимается в качестве расчетной.
