Глава V
НОРМА ГОДОВОГО СТОКА
При гидрологических и водноэнергетических расчетах ГЭС необходимо располагать данными о величинах расходов воды в реке в течение длительного периода, о характере колебаний расходов в пределах года, а также о распределении стока по сезонам, месяцам и суткам.
Расходы воды в реке колеблются из года в год около некоторого среднего значения, отклоняясь от него в отдельные годы довольно значительно.
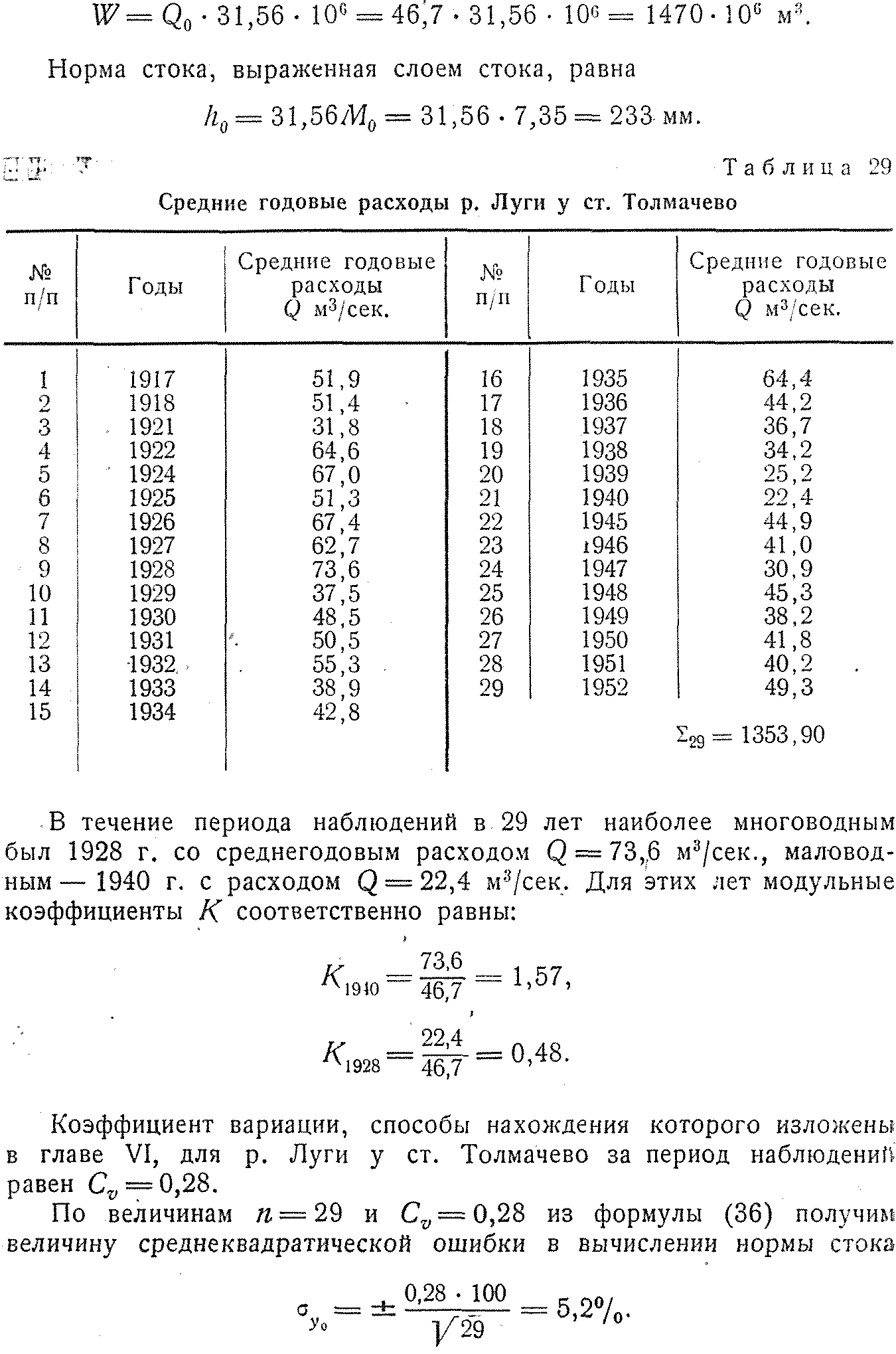
Средняя арифметическая величина из ряда величин годового стока за достаточно длительный период представляет собой средний многолетний сток или норму годового стока.
Норма годового стока может быть выражена в различных единицах измерений: в виде расхода, объема стока, модуля стока или высоты слоя стока.
При расчетах стока употребляются следующие общепринятые единицы стока.
- Расход Q — величина стока в секунду; выражается в м3/сек. Расходы могут быть также выражены в виде среднего секундного стока за несколько лет, за год, месяц, сутки и любой другой период.
- Модуль стока М — величина расхода воды с единицы водосборной площади; так же, как и расход, модуль стока может характеризовать средний расход за любой период времени — месяц, сезон, год и т. д. и измеряется в м3/сек. с 1 км2 или в л/сек. с 1 км2; чаще применяется последнее выражение. Зависимость между модулем стока и расходом представляется в следующем виде:
![]() (25)
(25)
где Q — расход воды в м3/сек., F — площадь водосбора в км3, 1000 — переходный коэффициент, зависящий от единиц измерения.
- Объем стока W — суммарная величина стока за некоторый
период времени, зависящая от водности реки и продолжительности расчетного периода. Объем стока выражается обычно в кубических метрах (м3). Например, объем годового стока можно представить так:

Коэффициент стока всегда меньше единицы и величина его меняется для различных периодов. Коэффициент стока характеризует собой долю осадков, переходящих в сток.
Вычисленные значения коэффициентов стока для коротких периодов: месяца, сезона и даже года, не отражают действительного соотношения между осадками и стоком за эти периоды, так как сток в значительной мере обусловливается также осадками в предшествующий период времени.
Норма стока может быть вычислена тем точнее, чем большее число лет производились наблюдения и чем меньше колебания годового стока. Поскольку для вычисления нормы стока используются данные статистического ряда наблюдений, величина вероятной погрешности в определении нормы стока может быть найдена с помощью закона распределения случайных ошибок.
Истинное среднее значение величины у из ряда значений наблюденных величин у может быть получено при условии безграничного возрастания числа членов п ряда наблюдений

Используя формулу (36), можно установить значение среднеквадратической ошибки среднеарифметической величины нормы годового стока в зависимости от числа лет наблюдений и коэффициента вариации Cv.
Эти значения, вычисленные Б. Д. Зайковым и С. Ю. Белинковым, приведены в табл. 28.
Приведенные в табл. 28 результаты показывают величины средних ошибок, которые могут быть получены при данном числе лет наблюдений. Однако любой конкретный рассматриваемый период может оказаться многоводным или маловодным. В этом случае ошибка в определении нормы стока может значительно превышать среднюю величину ошибки.
Таблица 28
Число лет наблюдений, необходимое для вычисления нормы стока с заданной точностью

Наименьшее число лет, необходимое для вычисления нормы стока с заданной точностью, в значительной мере зависит также от коэффициента вариации Сv годового стока. Так, например, для вычисления нормы стока с точностью 15% при Сv=0,15 необходимо располагать рядом наблюдений длительностью 9 лет; при % = 0,5 такая же точность может быть получена при длительности наблюдений 100 лет.
§ 19. Вычисление нормы годового стока при достаточно длительном периоде наблюдений

Эта же характеристика стока может быть представлена в виде объема стока