Для определения параметров и проектирования режимов работы сельскохозяйственных гидроэлектростанций определение многолетних колебаний стока и его распределения по месяцам оказывается недостаточным.
Хронологический ход колебаний стока по сезонам и месяцам дает возможность оценить распределение энергоресурсов реки в годовом разрезе по этим периодам. Однако определение мощности ГЭС и подсчеты возможной выработки электроэнергии гидростанций, производимые по среднемесячным расходам, создают неправильное представление об эффективности проектируемой ГЭС.
Дело в том, что определение расчетных расходов ГЭС по среднемесячным данным может быть оправдано лишь при наличии достаточных регулирующих емкостей, обеспечивающих месячное регулирование стока. В большинстве случаев сельскохозяйственные гидроэлектростанции имеют суточное регулирование стока, в силу чего расходы воды в течение месяца, превышающие средние месячные, не могут быть использованы и должны сбрасываться. Расходы ниже среднемесячных не обеспечивают расчетной мощности ГЭС, принятой по среднемесячным данным. Кроме того, при наличии сбросов уровни нижнего бьефа гидростанции повышаются, уменьшая напор и уменьшая тем самым мощность ГЭС против расчетной, установленной по среднемесячным расходам.
Таким образом, фактическая мощность ГЭС оказывается заниженной по сравнению с расчетной и в случае расходов, превышающих средние месячные, и в случае расходов ниже средних месячных.
Ввиду этого возникает необходимость в использовании данных о средних суточных расходах воды и их обеспеченности в течение года.
Кривые обеспеченности суточных расходов воды не выражают хронологическое изменение расходов в течение года, но дают возможность определить продолжительность периода, в течение которого имеют место расходы воды в реке, превышающие заданную величину или равные ей.
Если расположить средние суточные расходы воды за все годы наблюдений в убывающем порядке от абсолютного максимума до абсолютного минимума и по эмпирической формуле вычислить величину обеспеченности каждого расхода, то по этим данным может быть построена обобщенная или абсолютная кривая обеспеченности суточных расходов.
Построив кривые обеспеченности средних суточных расходов для каждого года наблюдений в отдельности путем осреднения ординат этих кривых, можно получить среднюю кривую обеспеченности.
Обобщенная кривая обеспеченности, характеризуя собой распределение средних суточных расходов в многолетнем периоде, не отражает особенностей колебаний среднесуточных расходов каждого года в отдельности. В свою очередь ни один из годов в силу многообразия условий стока не может содержать абсолютного максимума и абсолютного минимума многолетнего периода и в целом повторять картину многолетнего изменения суточных расходов.
Средняя кривая обеспеченности, занимая промежуточное положение между обобщенной кривой и годовыми кривыми обеспеченности, также не выражает реального распределения расходов внутри отдельных лет, но показывает некоторое типовое распределение среднесуточных расходов данной реки в течение среднего по водности года. Сопоставление обобщенных и средних кривых обеспеченности показывает, что обе эти кривые в пределах обеспеченностей примерно от 10 до 90% довольно близко совпадают между собой и расхождение между величинами средних суточных расходов не превышает 15— 18%. Таким образом, в пределах обеспеченностей, обычно используемых при водноэнергетических расчетах ГЭС, в равной мере возможно использование как обобщенной, так и средней кривой обеспеченности.
В практике проектирования сельских ГЭС предпочтение отдается средней кривой обеспеченности, так как для ее построения достаточно использования величин абсолютного максимума, абсолютного минимума и расходов, обеспеченных 30, 90, 180 и 270 дней в году, или соответственно 8, 3, 25, 50, 75% обеспеченности. Эти данные за каждый год наблюдений имеются в „Материалах по режиму рек“.
Рассмотрим пример построения средней кривой обеспеченности средних, суточных расходов воды р. Шелони у д. Заполье. Все ежедневные расходы воды за каждый год наблюдений 1938—1940 и 1945—1952 гг. располагаем в убывающем порядке и находим их величины обеспеченностью 30, 90, 180, 270 и 365 дней, которые соответствуют порядковым номерам в убывающем ряду средних суточных расходов за год. Эти данные и величины наибольших и наименьших в году суточных расходов, помещенные в табл. 70, могут быть использованы для построения кривых обеспеченности суточных расходов за каждый год.
Таблица 70
Ежедневные расходы воды различной обеспеченности р. Шелони у д. Заполье (в м3/сек.)

Ординаты средней кривой обеспеченности суточных расходов, получаемые осреднением соответствующих ординат годовых кривых обеспеченности, помещены в табл. 71. Величины ординат выражены в м3/сек. и в модульных коэффициентах, полученных как отношение величин средних суточных расходов данной обеспеченности к норме годового стока Q0=45,8 м3/сек. Это позволяет производить сравнительную оценку характера распределения средних суточных расходов воды различных рек.
По данным табл. 71 строим кривую обеспеченности средних суточных расходов р. Шелони у д. Заполье (рис 53, кривая 7), откладывая их по оси ординат в виде модульных коэффициентов. Величины максимального и среднего из максимальных модульных коэффициентов откладываем непосредственно по оси ординат; значениям среднего и наименьшего минимума присваивается обеспеченность 365 дней.
Обеспеченность, откладываемая по оси абсцисс, выражена в долях и в процентах от длительности года.
Пользуясь построенной кривой обеспеченности, можно определить величину среднего суточного расхода любой заданной обеспеченности или, наоборот, найти обеспеченность заданного среднесуточного расхода. Для сравнения обеспеченности величин среднесуточных и суточных расходов, определяемых по средней кривой обеспеченности и по кривой продолжительности среднемесячных расходов, последняя также показана на рис. 53 в виде ступенчатой линии 2.
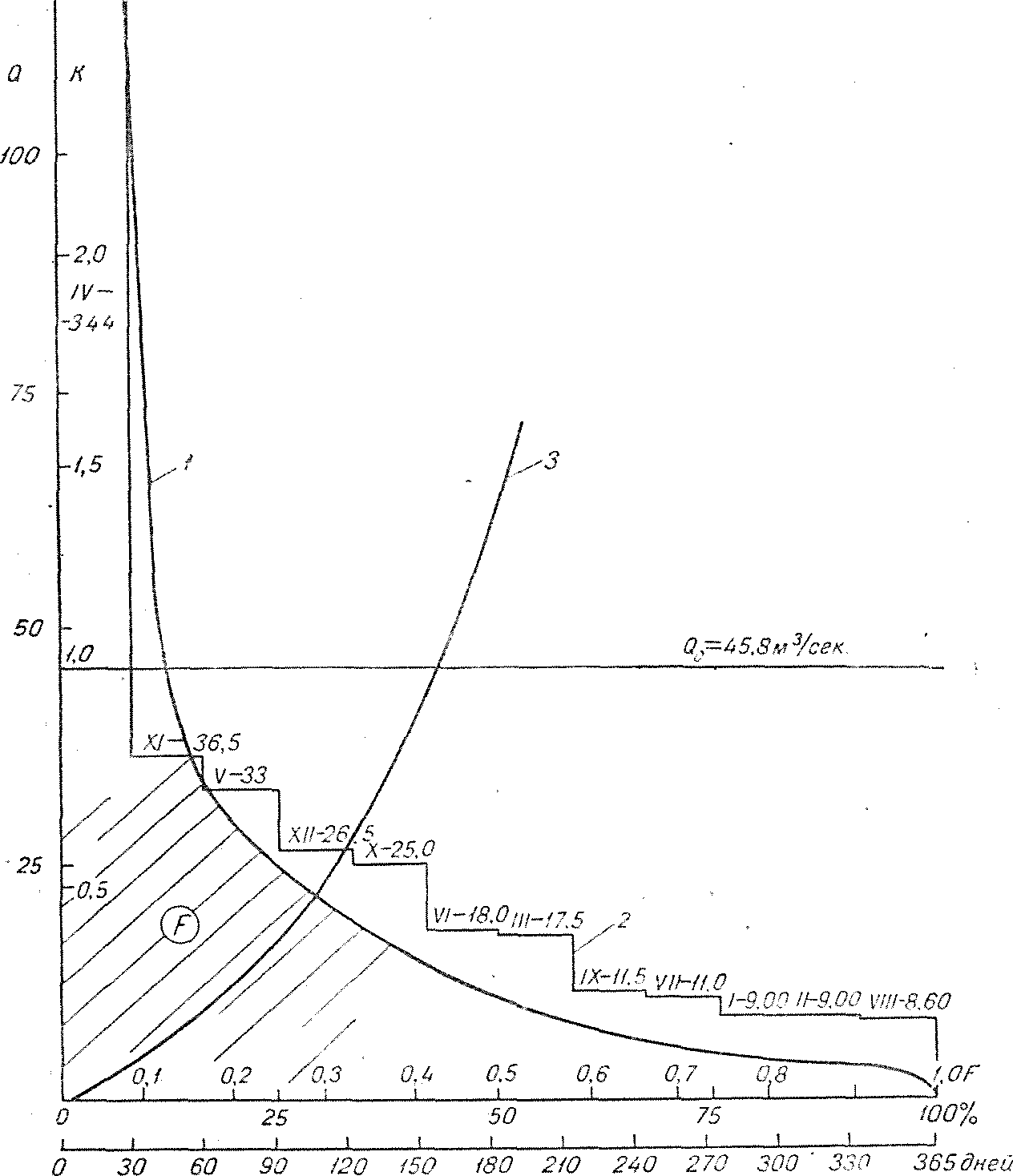
Рис. 53. Кривая обеспеченности и кривая использования стока р. Шелони у д. Заполье.
1 — средняя кривая обеспеченности ежедневных расходов, 2 — график продолжительности среднемесячных расходов, 3 — интегральная кривая использования стока.
Отсюда видно, что, начиная примерно с обеспеченности 30% и выше, т. е. в зоне энергетического использования стока, средние месячные расходы имеют большую величину, чем средние суточные такой же обеспеченности. Таким образом, расчетные параметры ГЭС, вычисленные по среднемесячным расходам, оказываются завышенными по сравнению с возможными по условиям стока.
Если площадь, ограниченную координатными осями и средней кривой обеспеченности суточных расходов, разбить горизонтальными линиями на ряд элементарных площадок, то площадь каждой такой площадки будет выражать собой величину стока за определенный период времени. Последовательно суммируя с нарастающим итогом величины отдельных площадок, можно построить интегральную кривую использования стока (рис. 53, кривая 3). По оси ординат откладываются величины модульных коэффициентов или расходов, а по оси абсцисс — доли от площади, заключенной между средней кривой обеспеченности и координатными осями. Величина этой площади принимается равной единице или 100%, а величины элементарных площадок выражаются в долях или в процентах от величины площади, ограничиваемой кривой обеспеченности. Интегральная кривая показывает величину использования годового стока при заданной расчетной величине среднего суточного, расхода и позволяет оценить степень энергетического использования энергии реки.
Таблица 71
Ординаты средней кривой обеспеченности суточных расходов р. Шелони у д. Заполье

Так, например, при расчетном расходе ГЭС Q = 50 м3/сек. (модульный коэффициент К=1,09), обеспеченном на 10%, годовой сток р. Шелони используется на 43%; при расходе ГЭС Q = 5 м3/сек., обеспеченном на 77%, сток реки используется на 7% и т. д.
При отсутствии гидрологических наблюдений на исследуемой реке кривая обеспеченности суточных расходов может быть построена по материалам для изученной и сходной по водному режиму реки-аналога. В этом случае находят ординаты средней кривой обеспеченности для аналога и выражают их в модульных коэффициентах. Эти ординаты принимают для построения кривой обеспеченности суточных расходов изучаемой реки. Затем определяется норма годового стока для рассматриваемой реки и перемножением ее на величины модульных коэффициентов максимальных, минимальных расходов и расходов, обеспеченных в течение 30, 90, 180, 270, 365 дней, находятся величины среднесуточных расходов воды соответствующей обеспеченности в расчетном створе.
Некоторыми авторами предприняты попытки выражения средней кривой обеспеченности суточных расходов посредством эмпирических формул. Эти формулы, полученные на основании анализа водного режима большого числа крупных рек, в общем удовлетворительно описывают средние кривые обеспеченности этих рек. Однако применение их к неисследованным, особенно малым рекам не дает надежных результатов из-за приближенности оценки входящих в эти формулы величин, таких, как средние годовые максимум и минимум расходов, параметров, зависящих от физико-географических характеристик водосбора, и т. п.
В силу этого указанные формулы в практике проектирования сельских ГЭС применения не получили.

