2. БЕЗРАЗМЕРНЫЕ ФОРМУЛЫ ДЛЯ ГИДРАВЛИЧЕСКИ ГЛАДКИХ И ШЕРОХОВАТЫХ РУСЛ
В 1913 г. Блазиус ввел понятие гладких и шероховатых труб. Им же была установлена однозначная зависимость коэффициента λ для гладких труб от числа Рейнольдса Re в виде


Рис. 1. Зависимость коэффициента гидравлического трения от числа Рейнольдса и относительной шероховатости (опыты Никурадзе):
I — линия Пуазейля; П — линия Блазиуса; III — линия равных r/k
Коэффициенты в этой формуле были установлены на основании опытов Никурадзе над трубами с искусственной равномерно зернистой шероховатостью (рис. 1). Впоследствии было введено понятие о так называемой эквивалентной равномерно зернистой шероховатости кэ, под которой понимают такую высоту выступов песка Никурадзе, которая создает сопротивление, равное действительному сопротивлению испытываемого трубопровода. Для определения эквивалентной равномерно зернистой шероховатости можно воспользоваться формулой (И), переписав ее в виде
![]() (12)
(12)
Зная диаметр d трубопровода и найдя значение коэффициента гидравлического трения λ (из опытов в квадратичной области), из этой формулы находят кэ. Таким образом, эквивалентная равномерно зернистая шероховатость кэ устанавливается не измерением высоты выступов, а по данным гидравлических испытаний трубопровода; ее поэтому часто называют также гидравлической шероховатостью.
Эквивалентная равномерно зернистая шероховатость характеризует не только среднюю высоту бугорков шероховатости, но также их форму, распределение по поверхности стенки и т.д. Отношение действительной высоты выступов k0 к высоте эквивалентной равномерно зернистой шероховатости кэ для различных поверхностей может колебаться в широких пределах. Для естественных шероховатостей [2] kэ/k0 =0,1:10. Для искусственных шероховатостей пределы колебания отношения kэ/k0 еще более значительны. Для равномерно зернистой шероховатости, испытанной Никурадзе, k0= кэ.
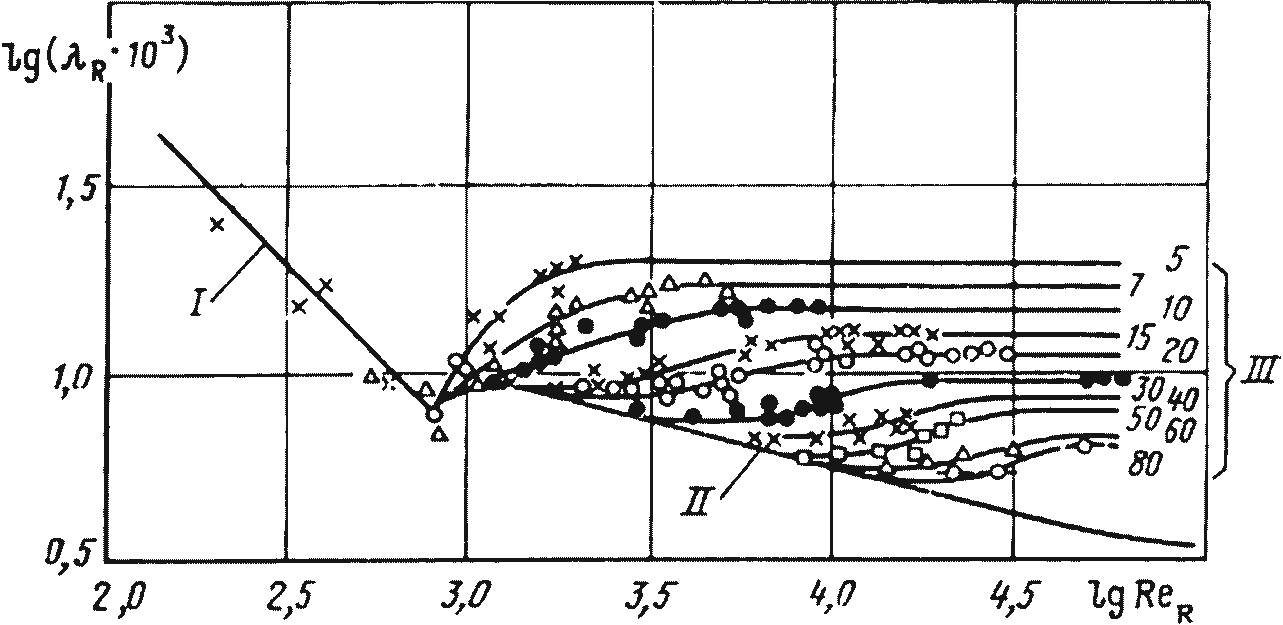
Рис. 2. Зависимость коэффициента гидравлического трения от числа Рейнольдса и относительной шероховатости (опыты А.П. Зегжды):
I - линия Пуазейля; II - линия Блазиуса; III - линии равных r/k, обозначенные цифрами у кривых
После того как в результате исследований Прандтля, Кармана и Никурадзе были получены рациональные формулы (10) и (11) для коэффициента гидравлического трения в круглых трубах, возник вопрос, можно ли и допустимо ли с физической точки зрения переносить формулы Прандтля на открытые потоки. Течение в открытых руслах отличается от течения в круглых напорных трубах по меньшей мере в двух отношениях: во-первых, в открытых руслах касательные напряжения распределены неравномерно вдоль границ потока в противоположность круглым трубам; во-вторых, благодаря наличию свободной поверхности в открытых руслах имеется трение на этой поверхности с соответствующим уменьшением поверхностных скоростей, а в некоторых случаях возникают дополнительные сопротивления, вызванные образованием волн.
Из-за отсутствия достаточных знаний о факторах, определяющих закономерности движения воды в открытых руслах, многие авторы на первых порах считали возможным пренебрегать особенностями движения в них и рекомендовали использовать для расчета открытых русл закономерности, найденные для напорных круглых труб, переходя от диаметра трубы к гидравлическому радиусу. Для уточнения этого предположения были поставлены экспериментальные исследования, в том числе опыты Зегжда [15, 16], которые проводились в лотке длиной 18 м и шириной 60,5 см. Изменяя уклоны, глубину и ширину потока с одной стороны и размер равномерно зернистой шероховатости, А.П. Зегжда получил график, изображенный на рис. 2.
По своему характеру кривые А.П. Зегжды аналогичны кривым Никурадзе, причем сходство этих графиков не ограничивается лишь качественной стороной: налицо достаточно хорошее количественное совпадение. Так, для прямоугольного лотка А.Л. Зегжда получил формулу
![]() (13)
(13)
близкую к формуле (11). Столь же хорошее совпадение было получено и для других областей: гладкого русла и переходной области, предшествующей квадратичному сопротивлению.

