16. ГИДРАВЛИЧЕСКОЕ МОДЕЛИРОВАНИЕ НАПОРНЫХ ВОДОВОДОВ [2]
При проектировании напорных водоводов электростанций во многих случаях, особенно при решении наиболее ответственных задач, возникает необходимость в проведении их испытаний на моделях1. Ниже излагается методика проведения модельных испытаний водоводов, основанная на использовании обобщенной формулы коэффициента гидравлического трения (17).
Гидродинамическое подобие между моделью и натурой в общем случае, как известно, обеспечивается при соблюдении закона подобия Ньютона

т.е. скорость на модели должна быть в L раз больше скорости в натуре.
1 Вопрос о гидравлическом моделировании энергетических объектов (в том числе напорных и открытых потоков) широко освещен в [25].
Моделирование напорных водоводов в соответствии с уравнением (73) связано с некоторыми неудобствами. Во-первых, использование уравнения (73) требует, чтобы геометрическое подобие между натурой и моделью было распространено и на выступы шероховатости; с практической точки зрения это требование может оказаться выше технических возможностей лаборатории. Наконец, предположение о том, что силы трения действуют по закону вязкости Ньютона, на основании которого получено уравнение (73), при турбулентном течении уже не является, как известно, справедливым, в связи с чем уравнение (73) может оказаться недостаточным для характеристики подобия. На практике поэтому уравнением (74) пользуются редко, прибегая к приближенным методам моделирования.
К вопросу о моделировании водоводов можно, однако, подойти и несколько отличным образом. Запишем отношение между силами инерции и силами трения в виде:

Итак, подобие обеспечивается равенством коэффициентов гидравлического трения.
Условие (77) достаточно для обеспечения гидравлического подобия даже в тех случаях, когда отсутствует геометрическое подобие шероховатости. Действительно, как было показано [1], распределение скоростей в трубах определяется значением коэффициента гидравлического трения λ вне зависимости от значений числа Рейнольдса или относительной шероховатости.
Найдем соотношения, которым должны удовлетворять элементы двух гидравлически подобных систем, находящихся под действием сил турбулентного трения. Будем исходить из равенства (77), причем для коэффициента гидравлического трения примем полученную выше обобщенную степенную формулу (17).
С учетом (17) формула (77) принимает вид


Таким образом, правилом Рейнольдса можно пользоваться для очень гладких поверхностей и в случае, когда геометрическое подобие распространено на шероховатость.
Рассмотрим основные задачи, возникающие при моделировании равномерного движения в длинном напорном водоводе.
Первая задача состоит в оценке коэффициента гидравлического трения, которым обладает рассматриваемый водовод в действительности при характерной для него скорости vн. Для этого производится лабораторное исследование гидравлического сопротивления модели достаточно длинного участка водовода, сделанной из того же материала, что и натурный водовод, но значительно меньшего диаметра. По результатам этого исследования с помощью формулы (17) определяется эквивалентная шероховатость kн рассматриваемого материала, после чего по той же формуле подсчитывается значение коэффициента гидравлического трения λн для натурного водовода. Можно также, выбрав значение kн для заданного материала по табличным данным, определить по уравнению (84) скорость на модели, при которой коэффициент гидравлического трения
на модели будет равен коэффициенту гидравлического трения в натуре, и из опытов на модели найти его значение. Если расчет по формуле (84) приводит к отрицательному значению для vм, то это означает, что ни при какой скорости в модели выбранного масштаба нельзя добиться гидравлического подобия между моделью и натурой.
Вторая задача состоит в создании модели существующего водовода, диаметр которого dн, скорость мн и коэффициент гидравлического трения λн известны. Устройство модели может оказаться целесообразным для облегчения исследования условий работы натурного водовода, например для изучения распределения скоростей по сечению. Для этого, задавшись масштабом модели L, по формуле (81) определяется скорость на модели vм, при которой λм= λн. После создания на модели этой скорости ее корректируют, чтобы замеренный на модели коэффициент гидравлического трения λм был равен коэффициенту гидравлического трения натуры λн. Тогда распределение скоростей в модели и натуре будет подобным.
Третья задача вытекает из условия геометрического подобия

Из этого уравнения при заданном масштабе модели L можно определить необходимую шероховатость модели kм, а при заданной шероховатости модели — ее масштаб. Пересчет в натуру результатов, полученных на модели, можно производить по уравнению (87), т.е. по правилу
Фруда. Для случая, когда νн=νм, уравнение (88) приводится к виду
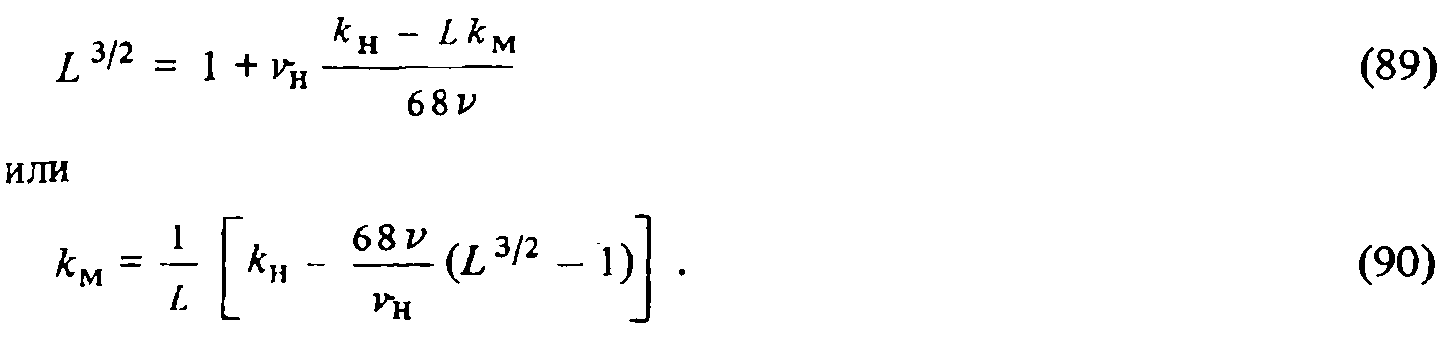
Если в модели используется гидравлически гладкая (например, латунная) труба kм=0, то из (89) получим
![]()
(91)
Из изложенного видно, что для приближенного моделирования нет необходимости выполнять модель водовода геометрически подобной натуре в отношении мелких неровностей ее стенок и добиваться одинаковой с натурой относительной шероховатости, что чрезвычайно затруднительно; нет также необходимости добиваться на модели чисел Рейнольдса, одинаковых с натурой или лежащих в автомодельной области. Моделирование в соответствии с уравнением (77) возможно на трубопроводе из другого материала, чем в натуре, и при меньших числах Рейнольдса.

