При процессах, происходящих в активных зонах реакторов, и при ядерных реакциях на ускорителях образуются различные частицы: нейтроны, электроны, протоны, альфа-частицы, осколки деления, гамма-кванты и мезоны. Проникающая способность всех этих частиц не одинакова. Так как электроны, протоны, альфа-частицы и осколки деления имеют электрический заряд, они быстро тормозятся в сравнительно тонких слоях вещества. Например, пробег наиболее пропинающей из перечисленных частиц, электрона, энергии 5—6 Мэе в алюминии равен приблизительно 1 см [35]. Основную опасность за толстыми слоями защиты представляют нейтральные частицы — нейтроны и гамма- кванты. Только эти частицы обычно учитываются при расчетах биологической защиты [3, 6, 24, 361, поэтому о них в дальнейшем и будет идти речь.
Однородные среды
Рассмотрим простейшую схему распространения частицы (нейтрона и гамма-кванта) в бесконечной однородной среде. Предположим, что эти частицы испускаются точечным источником, расположенным внутри среды. Для расчетов будем пользоваться следующими величинами: х — расстояние от источника до точки, в которой подсчитывается поток частиц; Ф — поток частиц, т. е. число частиц, пересекающих сферу с сечением в диаметральной плоскости единичной площади в единицу времени; λ — длина свободного пробега частицы до соударения с атомами среды.
Если мощность источника q (число частиц, образующихся в единицу времени), то поток ни разу не столкнувшихся с атомами среды частиц на расстоянии х от источника
![]() (1.3)
(1.3)
Длина свободного пробега частиц зависит как от их типа, так и от энергии.
По формуле (1.3) можно определить поток нерассеянных частиц, т. е. поток частиц с начальной энергией Е0. Проходя через защиту, гамма-кванты и нейтроны взаимодействуют со средой; в результате часть из них поглощается, часть замедляется. Таким образом, в каждой точке среды образуется спектр частиц по энергиям в интервале от нулевой до начальной энергии Е0.
Суммарный поток частиц Ф можно определить, если известно отношение полного потока частиц в данной точке среды к потоку нерассеянных частиц Ф0. Это отношение обычно называют численным фактором накопления. Оно характеризует число частиц в данной точке, накопившихся в результате процессов рассеяния и замедления. Суммарный поток частиц всех энергий в этом случае запишется так:
![]() (1.4)
(1.4)
Аналогичное выражение можно записать для потока энергии или мощности дозы в данной точке среды. Только в этом случае оно будет включать энергетический Вэ или дозовый Bд, факторы накопления и энергетическую qэ или дозовую qд мощности источника.
![]()
Для источников моноэнергетических нейтронов фактор накопления, например численный, можно представить в экспоненциальной форме:
(1.5)
где ввиду слабой зависимости В и β от х можно считать, что В да да const и β да const для больших х. Тогда формула (1.4) перепишется в виде
![]() (1.6)
(1.6)
Экспериментально установлено, что для источников моноэнергетических нейтронов или гамма-квантов на больших расстояниях в защите распределения Ф · х2 носят приблизительно экспоненциальный характер, а вблизи источника имеется характерное слабое уменьшение потока, связанное с установлением равновесия в спектре замедляющихся частиц. Величина, называемая длиной релаксации, слабо зависит от толщины защиты и является функцией свойств защитной среды и энергии нейтрона или гамма-кванта [6, 36, 37]. В расчетах эта величина используется обычно для вычисления потоков быстрых нейтронов, так как для гамма-излучения достаточно хорошо рассчитаны и протабулированы значения факторов накопления [3, 24, 36]. Длина релаксации связана с длиной свободного пробега соотношением:
![]() (1.7)
(1.7)
Коэффициент а характеризует долю полного сечения, которая эффективно участвует в ослаблении защитой потока нейтронов. В третьей главе приведены измеренные абсолютные значения а для некоторых веществ.
Численный коэффициент В называют фактором первоначального накопления нейтронов [36]. Он характеризует появление в потоке быстрых нейтронов вблизи источника замедленных нейтронов, которые вносят в поток все больший вклад.
Необходимо отметить, что по формуле (1.6) вычисляется поток не всех нейтронов, а лишь с определенной энергией, включая частицы начальной энергии. Эта группа нейтронов является обычно в легких средах наиболее проникающей — ведущей. Соответственно Вч и λ вычисляются для определения накопления и ослабления только этой группы. Предполагается, что остальные, более медленные частицы (частицы с меньшей энергией), появившиеся в результате замедления частиц ведущей группы, приходят из областей, близких к рассматриваемой точке, и в силу своей малой проникающей способности существенно не влияют на величину длины релаксации. Значит, пространственное распределение частиц характеризуется ведущей группой, а замедленные частицы лишь увеличивают число частиц в каждой точке. Это увеличение потока или накопление сильно замедленных частиц обозначим β [3, 36, 38], тогда
![]() (1.8)
(1.8)
В тех случаях, когда частицы, испускаемые источником, не монохроматические, а распределены в спектр, суммарный поток (дозу) можно определить интегрированием по энергии, т. е.
![]() (1.9)
(1.9)
Если для источников монохроматических частиц на больших расстояниях от них длина релаксации слабо зависит от расстояния [37, 38], то для немонохроматических источников это не так. В этом случае различные группы нейтронов обладают разной проникающей способностью. Наиболее проникающие определяют распределение на больших толщинах защиты, менее проникающие, если их образуется в источнике много, преобладают на малых толщинах. Поэтому длина релаксации частиц немонохроматических источников есть функция расстояния по всей толщине защиты.
Задача расчета защиты осложняется еще тем, что реальный источник радиации, которым является, например, активная зона реактора, не только создает нейтроны и гамма-кванты, распределенные в сложные энергетические спектры, но и представляет собой объемный источник. Таким образом, применение простейших выражений (1.4—1.9) возможно только при определении потоков частиц от отдельных небольших участков реального источника. Суммарные потоки можно найти как суперпозицию многих точечных источников (см. разд. 2.2), т. е.
![]() (1.10)
(1.10)
где г — расстояние между излучающим элементом источника и точкой, в которой определяется поток.
Многослойная и многокомпонентная защита
Для расчета потоков быстрых нейтронов в многослойной защите и защите из смеси легких и тяжелых элементов удобно применять эмпирический метод сечений выведения [3, 24]. Сущность его заключается в следующем. Если в водородсодержащей среде ί каких-либо веществ, то потоки быстрых нейтронов (предположим, что это нейтроны с Е > 1,5 Мэе) от моноэнергетического источника рассчитываются по следующей формуле:
![]() (1.11)
(1.11)
Здесь fн (х) — пространственное распределение быстрых нейтронов в водороде плотности, равной плотности водорода в защите [fн (х) = Ф (x) для водорода]; ϭirет, ni — сечение выведения i-ro вещества и число ядер ί-го вещества в единице объема.
Таким образом, вводится некий параметр — сечение выведения ϭrem. Оно имеет смысл эффективного сечения поглощения быстрых нейтронов в энергетическом интервале дельта Е = Е — Еп, где Еп — пороговая энергия. Нейтроны с энергией ниже Еп не учитываются. Энергия Еп может быть принята в легких средах равной, например, 1,5 Мэв. Сечение выведения складывается из сечения поглощения, большей части сечения неупругого рассеяния и части сечения упругого рассеяния за вычетом той его доли, которая связана с рассеянием нейтронов в некотором телесном угле в направлении вперед.
Для источника, излучающего нейтроны спектра S (Е), поток находится интегрированием выражения (1.11) по энергии:
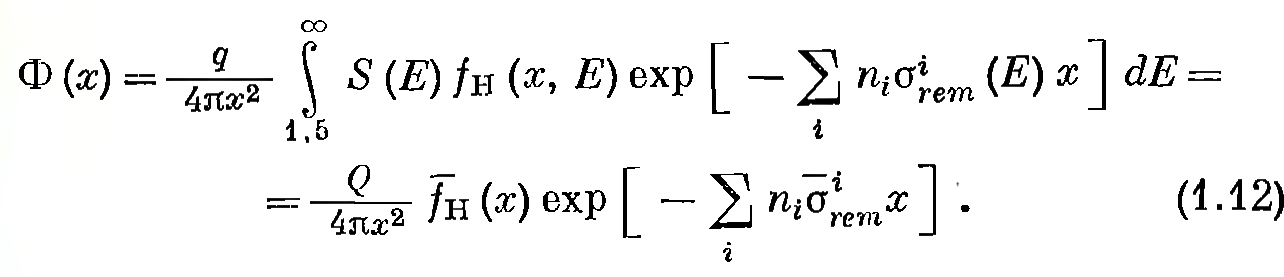
Можно найти потоки от источника нейтронов сложного спектра, разложив этот спектр на отдельные моноэнергетические составляющие.
В тех случаях, когда имеются рассчитанные или измеренные значения усредненных по этому спектру функций fн (х) и ϭrem, можно получать величину потока на основе второй части равенства (1.12).
Сечение выведения обычно находят экспериментально, однако существуют и методики их расчета [39]. Одно из выражений для источника нейтронов со спектром деления имеет весьма простой вид и хорошо согласуется с опытом:
![]() (1.13)
(1.13)
Здесь А — атомный вес ядра выводящего материала. Для сложных спектров применяют оба изложенных метода расчета.
Первый, использующий зависимость сечений выведения от энергии нейтронов, позволяет найти пространственные распределения потока нейтронов по всей защите, второй дает лишь суммарное ослабление за полной защитой при большой ее толщине.
Сейчас уже опубликовано много работ, посвященных измерению сечений выведения различных веществ как для источников моноэнергетических нейтронов, так и для источников нейтронов со спектром деления.
В работах [36, 37, 40, 41] доказано, что величина сечений выведения не меняется от способа введения выводящего вещества в легкую защиту (гомогенно или в виде блоков). Важно лишь, чтобы легкого вещества было достаточно для установления равновесного спектра. Роль основной легкой среды, кроме водорода, могут выполнять другие вещества с малым атомным весом. Если рассматривать группу нейтронов с энергией Е > 1,5 Мэв, то для среды замедлителя область допустимых атомных весов будет 1 < А < 27.
Для некоторых наиболее легких сред величина длины релаксации и обратная величина сечения выведения совпадают, если рассматривать нейтроны энергетического интервала Е > 1,5 Мэе. Такое совпадение выполняется, например, для воды и карбида бора [40]. Для более тяжелых сред это совпадение, по-видимому, отсутствует. Чтобы добиться совпадения, необходимо повысить энергетический порог рассматриваемой нейтронной группы [40, 41]. Если найдено пространственное распределение быстрых нейтронов, можно рассчитать потоки замедляющихся нейтронов. Эти расчеты чаще всего проводят многогрупповыми методами в различных приближениях метода сферических гармоник [36, 42].
Можно решить задачу и без задания ведущей группы. В этом случае применение многогрупповых методов дает хорошие результаты только при использовании Р-приближения и выше метода сферических гармоник [43].

