ГЛАВА СЕДЬМАЯ
РАСПРЕДЕЛЕНИЕ ТОКА ПО ЭЛЕМЕНТАМ ЭЛЕКТРИЧЕСКИХ АППАРАТОВ
7.1. Распределение тока в полюсах разъединителей коробчатого сечения
Полюс разъединителя коробчатого сечения может быть эквивалентирован полым токопроводом прямоугольного сечения, в частном случае квадратом. А это позволяет для расчета токораспределения по элементам разъединителя применить методику расчета, описанную во второй и четвертой главах.
Рассмотрим указанное токораспределение па примерах.
Пример 7.1. Уединенный полюс разъединителя. Ток I = 14 400 А. На рис. 7.1 представлено сечение полюса разъединителя в зоне неподвижных контактов. Показаны основные размеры. Сторона квадратного сечения а = 400 мм = 0,400 м: ордината точки А, отделяющей первый элемент от второго, д = 90 мм = 0,09 м. Считая поверхностный эффект резко выраженным, требуется определить распределение тока по неподвижным контактным элементам.
Решение. Пронумеруем восемь неподвижных контактных элементов. Удельная координата точки А у0 = д/(0,5а) = = 0,09/(0,5 · 0,4) = 0,45. Параметр 0 (см. §2.5) определяется из трансцендентного уравнения
![]()
из которого следует, что при у0 = 0,45; θ = 0,28; рад = 16°.
Удельный ток в элементе 1, расположенном на правой грани, I10 = θ/π =0,28/π = 0,089.
Удельный ток I10 в угловом элементе 2
I20 = 0,25—θ/π = 0,25—I10 = 0,25—0,089 = 0,161.
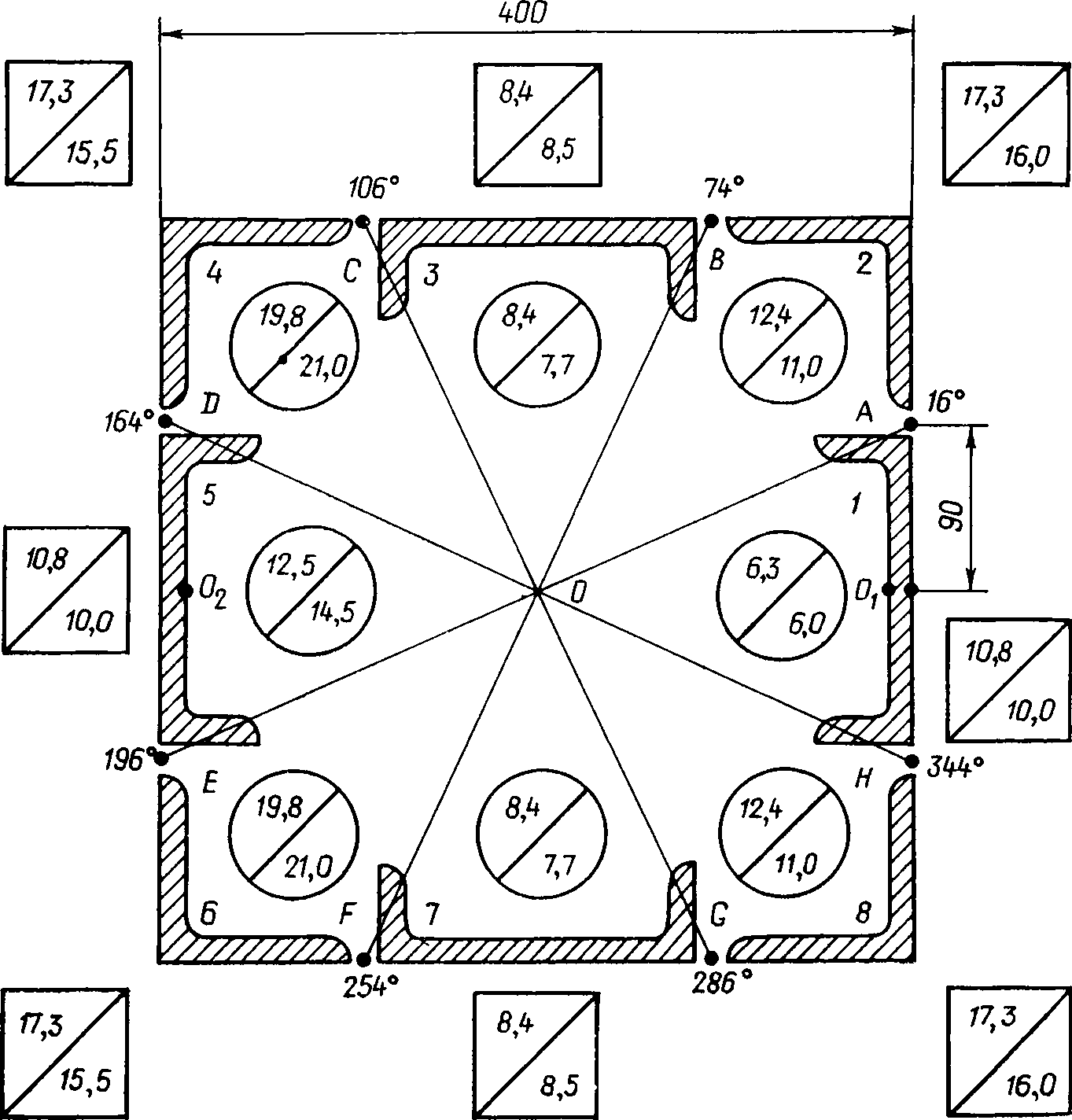
Рис. 7.1. Распределение тока по элементам полюса разъединителя коробчатого сечения
Ток I1 в элементе 1
I1 = I1 0I= 0,089х14 400 = 1281 А.
Ток I2 в элементе 2
I2 = I20I = 0,161х14 400 = 2318 А.
Благодаря симметрии I3 = I5 = I7 = I1 = 1281 А; I4 = I6 = I8 = I2 = 2318 А.
Ток в угловом элементе 2 оказался больше, чем в элементе Л вследствие поверхностного эффекта.
В однофазной системе указанная симметрия нарушается, поскольку на поверхностный эффект накладывается эффект близости. Проиллюстрируем это на примере.
Пример 7.2. Однофазная система разъединителей. Ток I = 14 400 А. На рис. 7.1 изображен один из полюсов однофазной системы, соответствующий правому ТЭ на рис. 1.2 (поз. 8). Его размеры показаны на рисунке: а = 400 мм = 0,4 м; у = 90 мм = 0,09 м. Расстояние между осями полюсов D = 1,2 м. Считая поверхностный эффект резко выраженным, требуется найти распределение тока по элементам полюса.
Решение. Пронумеруем восемь неподвижных контактных элементов. Благодаря симметрии относительно оси х ограничимся рассмотрением верхней половины полюса.
В точке Ο1 θ = 0, в точке О2 θ = π. Удельная ордината точек А и D уо = у/(0,5а) = 0,090/(0,5-0,4) = 0,45. Удельная абсцисса точек В и С х0В = 0,45; х0С = —0,45. Значения θ1 и θр, соответствующие границам первого и второго или четвертого и пятого элементов, найдем из трансцендентного уравнения ![]() отсюда
отсюда
![]()
Значения θВ и θС, соответствующие точкам В и С, ограничивающим третий элемент, определяются из трансцендентного уравнения
![]()
отсюда
![]()
Удельный ток![]() между произвольной точкой на верхней половине периметра сечения полюса и точкой О1 определяется соотношением
между произвольной точкой на верхней половине периметра сечения полюса и точкой О1 определяется соотношением
![]()
где Ιх — ток между указанными точками; Ι — общий ток в полюсе;
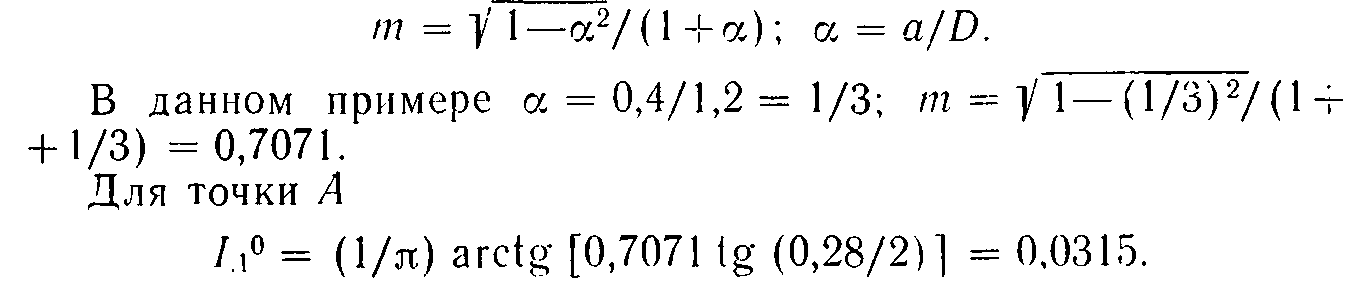
Для точки В
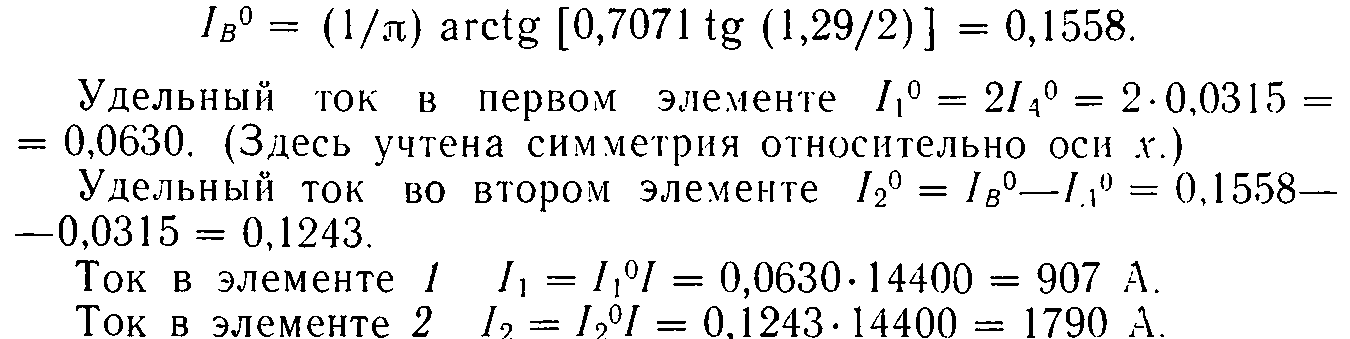
Данные расчета токораспределения по всем элементам сведены в табл. 7.1. Как уже указывалось, на рис. 7.1 показано токораспределение в правом полюсе однофазной системы. В кружках в числителе показано значение In0 в процентах. Для получения токораспределения в левом полюсе следует повернуть рисунок на 180°. На этом же рисунке показаны углы θ, соответствующие границам элементов, и отмечен номер каждого из элементов.
Таблица 7.1
Распределение тока по элементам полюса разъединителя в однофазной системе или в крайних фазах трехфазной системы А и С
Точка |
|
|
| Элемент |
|
|
о, | 0,00 | 0,00 | 0,0000 | 1 | 0,0630 | 907 |
А | 0,28 | 16 | 0,0315 | 9 | 0,1243 | 1790 |
В | 1,29 | 74 | 0,1558 | 3 | 0,0840 | 1210 |
С | 1,87 | 106 | 0,2400 | 4 | 0,1977 | 2847 |
D | 2,86 | 164 | 0,4375 | 5 | 0,1250 | 1800 |
Ch | 3,14 | 180 | 0,5000 | 6 | 0,1977 | 2847 |
Е | 3,42 | 196 |
| 7 | 0,0840 | 1210 |
F | 4,43 | 254 |
| 8 | 0,1243 | 1790 |
G | 4,99 | 286 |
|
|
|
|
Н | 6,00 | 344 |
|
|
|
|
Сумма | 1,0000 | 14 400 | ||||
7.2. Распределение тока по элементам полюсов трехфазной системы разъединителей
Ограничимся рассмотрением часто встречающегося варианта, когда все три фазы А, В и С расположены в одной горизонтальной плоскости (7 на рис. 1.3). Для приближенной оценки токораспределения в симметричной трехфазной системе токов пренебрежем взаимным влиянием фаз А и С и определим токораспределение в полюсах наложением двух однофазных систем АВ и ВС, сдвинутых по фазе относительно друг
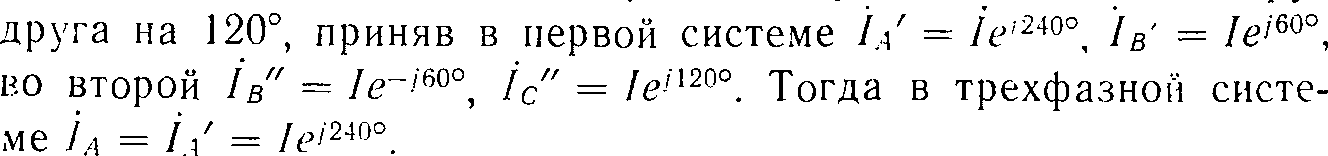
Исходя из принятого приближения будем считать, что распределение тока в крайних фазах А и С эквивалентно распределению тока в однофазных системах. Токораспределение в средней фазе В можно получить путем наложения распределения токов Iв и Iв". Рассмотрим это на примере.
Пример 7.3. Трехфазная система разъединителей. Ток в полюсе I = 14 400 А. На рис. 7.1 показан один из полюсов трехфазной системы. Его размеры показаны на рисунке: а = 400 мм = 0,400 м; у = 90 мм = 0,090 м. Расстояние между осями соседних полюсов D = 1,2 м. Считая поверхностный эффект резко выраженным, требуется найти распределение тока по элементам каждого из полюсов.
Решение. 1. Распределение тока в крайних фазах А и С эквивалентно токораспределению в однофазных системах. Оно приведено в табл. 7.1, где использован материал предыдущего примера.
На рис. 7.1 показано распределение тока по элементам фазы С. В кружках показано выраженное в процентах для каждого из восьми элементов отношение тока в элементе к общему току. Числитель соответствует расчету в соответствии с табл. 7.1, знаменатель — эксперименту, описанному в [5]. Для получения токораспределения в фазе А рисунок следует повернуть на 180°.
2. Ток в средней фазе В, рассчитанный по приведенным выше формулам, где используются данные табл. 7.1. распределяется по участкам 1, 2, 3 следующим образом:
![]()
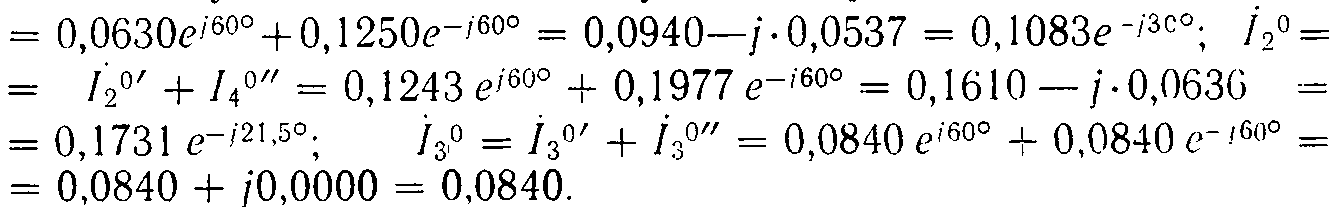
Таблица 7.2
Распределение тока по элементам полюса разъединителя в средней фазе трехфазной системы В
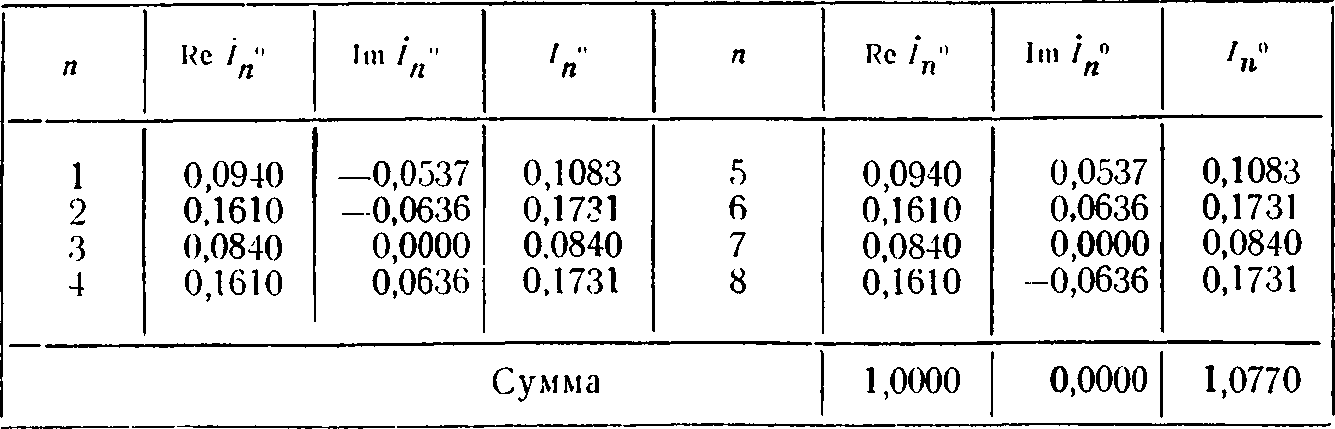
Симметрия позволяет найти токи Iп0 и на участках 4, 5, 6, 7, 8. Результаты расчета сведены в табл. 7.2. Отличие от единицы суммы в последнем столбце свидетельствует о наличии фазового сдвига между токами в отдельных элементах. На рис. 7.1 в квадратах показано распределение тока по элементам фазы В. Числитель соответствует расчету, знаменатель — эксперименту, описанному в [5].

