В трехфазных сетях до 1 000 В токи нагрузки чаще всего соизмеримы с токами однофазных замыканий на корпус и пренебрежение в расчетах токами нагрузки не позволяет получить истинную картину токораспределения в схеме.
Представим однофазную и трехфазную нагрузку условно сосредоточенной (рис. 4-18) и приняв за положительное направление токов направление к неповрежденным фазам, нетрудно увидеть, что на токораспределение влияет как неповрежденная статическая и динамическая нагрузка сети, так и нагрузка, на которой произошло замыкание на корпус.
Степень влияния этой нагрузки определяется ее мощностью и схемой включения в сеть. Первое обстоятельство очевидно (величиной мощности определяется номинальный ток нагрузки), второе будет подтверждено дальнейшим анализом.
Рассмотрим подробнее вопрос о токораспределении при однофазных замыканиях в трехфазной сети. Отметим прежде всего, что все возможные схемы включения электрической нагрузки в сеть (звезда, треугольник, однофазная нагрузка) можно путем несложных преобразований свести к двум расчетным схемам:
а) электрическая нагрузка связана в звезду, электрическая нейтраль которой изолирована от нулевого провода (рис. 4-18, а);
б) электрическая нагрузка связана в звезду, электрическая нейтраль которой связана с нулевым проводом через сопротивление нагрузки. Схема вытекает из преобразования электрической нагрузки, связанной треугольником, в звезду (рис. 4-18,б).
Рис. 4-18. Схема токораспределении в трехфазной электроустановке при однофазном замыкании на корпус с учетом нагрузки. а — электрическая нейтраль нагрузки изолирована от нулевого провода; б — электрическая нейтраль нагрузки связана с нулевым проводом.
Примем для упрощения выводов следующие допущения:
- пренебрегаем сопротивлениями питающей системы 6—10 кВ, автомата, трансформаторов тока и электрической дуги;
- питающую систему представляем источником неограниченной мощности (полагая
), что позволяет считать напряжение на выходе трансформатора неизменным за время короткого замыкания; - рассматриваем всю нагрузку как статическую, т. е. обладающую одинаковым сопротивлением токам прямой, обратной и нулевой последовательностей;
- пренебрегаем током, проходящим через сопротивление заземления нейтрали.
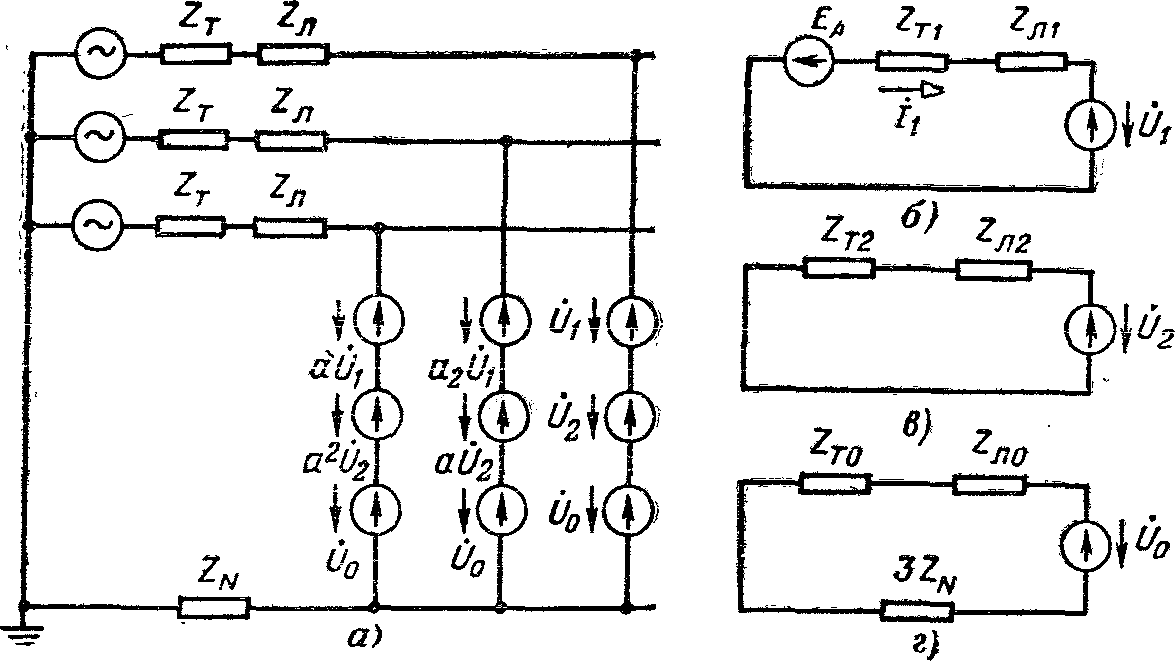
Рис. 4-19. Расчетные схемы зануления с учетом токов нагрузки.
а — принципиальная схема; б— схема прямой последовательности; в — схема обратной последовательности; г — схема нулевой последовательности.
Расчет тока однофазного к. з. в первой расчетной схеме (рис. 4-18, а) проведем методом симметричных составляющих с использованием принципа компенсации. Введем в схему в месте замыкания источник напряжения, создающий токи между фазовыми и нулевым проводами
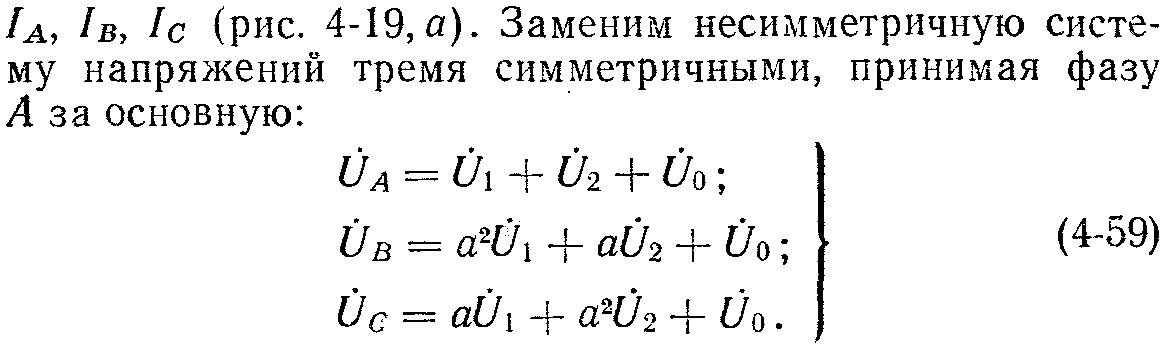
Аналогично заменяем несимметричную систему токов, после чего расчетную схему можно заменить тремя симметричными схемами (рис. 4-19, а, в, г). В каждой схеме токи определяются сопротивлениями элементов расчетной схемы каждой последовательности. Сопротивление нулевого провода включено утроенной величиной, так как по нулевому проводу проходят токи нулевой последовательности всех трех фаз.
Составим уравнения по второму закону Кирхгофа для схемы каждой последовательности:
Окончательно имеем систему уравнений, описывающих несимметричный режим в симметричной системе координат:
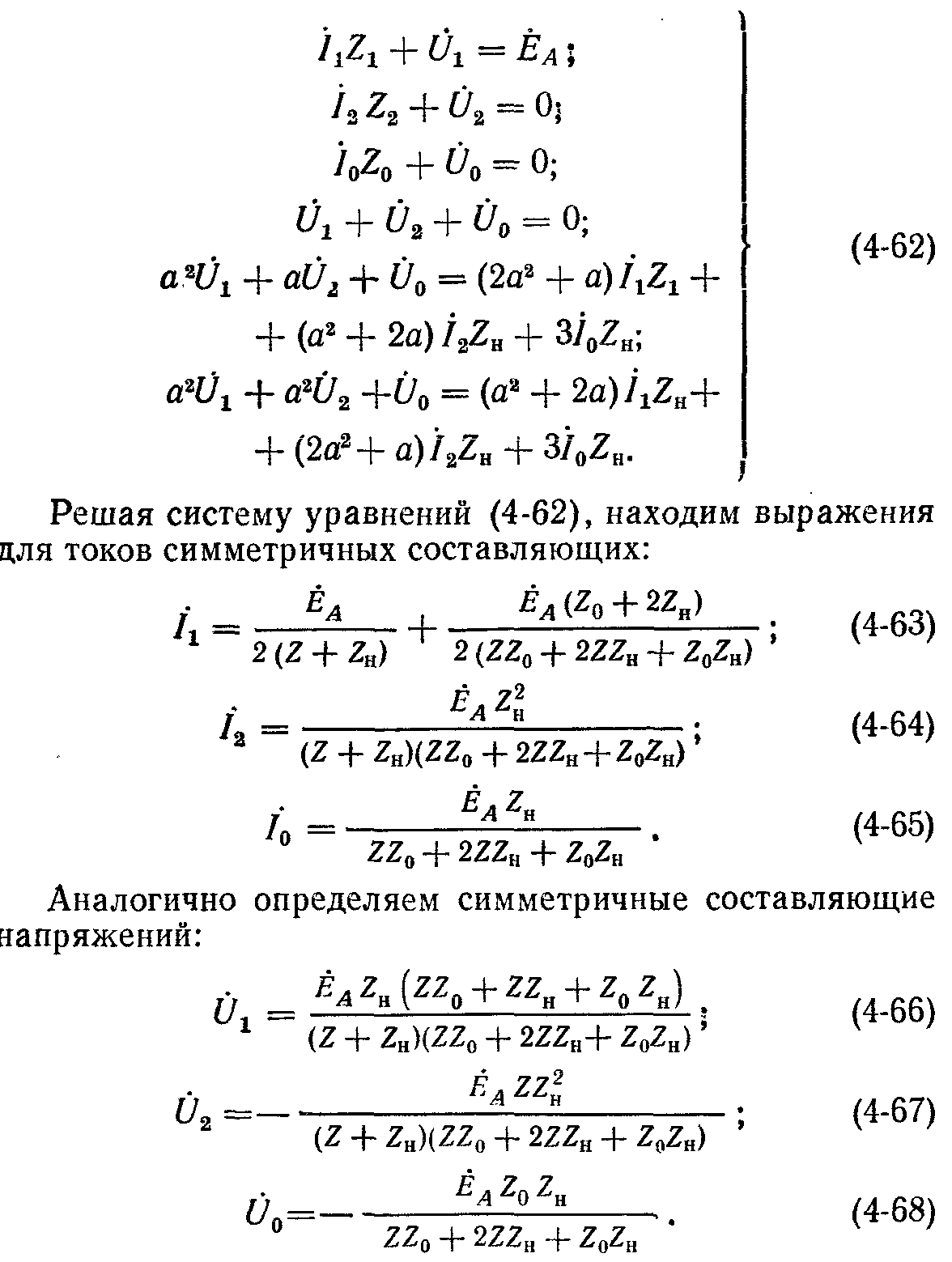
Выражения (4-63) — (4-68) позволяют определить токи и напряжения в исходной несимметричной схеме. Для этого достаточно воспользоваться принципом наложения. Ток в фазе А, равный току замыкания, будет определяться выражением
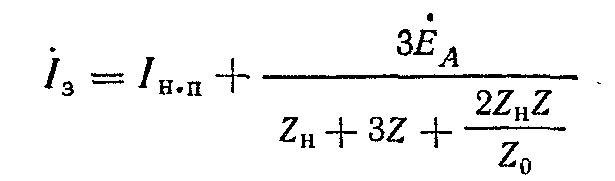
(4-83)
Второй член в уравнении (4-83) представляет утроенное значение тока приведенной эквивалентной нагрузки. Следовательно, ток замыкания превышает ток в нулевом проводе на величину утроенного тока нагрузки.
Для дальнейшего анализа представляет интерес также выражение для напряжения на нулевом проводе:
(4-84)
Выражением (4-84) в значительной мере определяется величина напряжений прикосновения.