В некоторых электроустановках можно рассматривать схему зануления как однофазную, т. е. при расчетах параметров зануления исходить из схемы однофазного короткого замыкания на корпус, представляющей простую «петлю» фазный провод — магистраль зануления. Такое допущение возможно для однофазных электроустановок и трехфазных электроустановок, в которых можно пренебрегать токами нагрузки по сравнению с токами короткого замыкания. Остановимся подробнее на оценке возможности применения однофазной расчетной схемы в трехфазных сетях. Для этого проведем анализ несимметричного режима, обусловленного однофазным замыканием на корпус, методом симметричных составляющих.
Основные положения метода расчета. В методе симметричных составляющих несимметричная система трехфазных величин (токов, напряжений и т. д.) представляется в виде суммы трех симметричных систем, величины которых принято называть симметричными составляющими прямой, обратной и нулевой последовательностей. Несимметричная система величин А, В, С выражается через ее симметричные составляющие соотношениями:
(4-9)
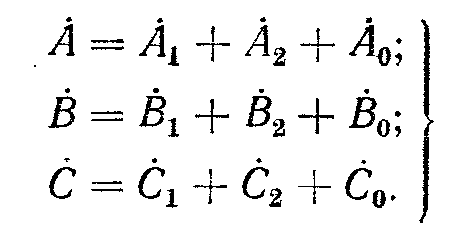
Кроме того, одну из несимметричных величин можно принять за основную, например А, тогда несимметричные составляющие двух других векторных величин выражаются через составляющие основного вектора А:
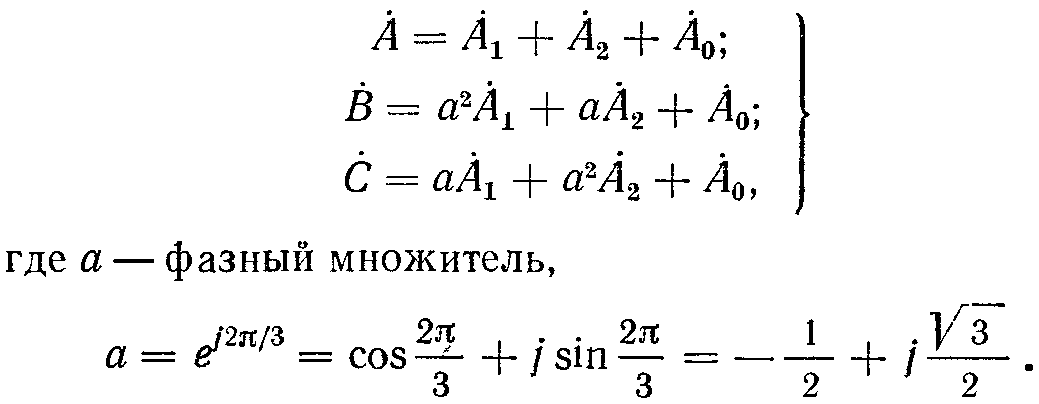
(4-10)
При расчете несимметричных режимов принимается следующая последовательность:
а) несимметричная система исходных величин представляется в виде трех симметричных систем, т. е. определяются симметричные составляющие несимметричной системы:
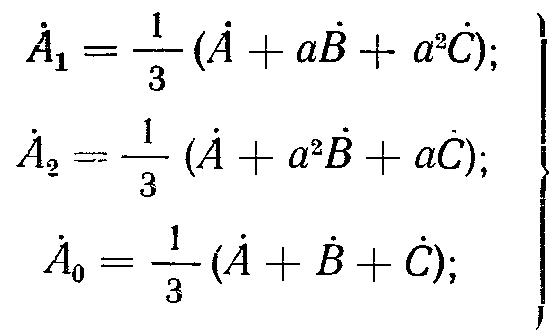
(4-11)
б) производятся преобразования над симметричными системами, предусмотренные условием задачи;
в) определяется реальная несимметричная система на основании тех значений симметричных составляющих, которые получены в результате преобразований.
Для расчетов несимметричных режимов в трехфазных электроустановках удобно пользоваться принципом компенсации, заменяя несимметричную нагрузку или несимметричный участок в сети источником напряжения. С этой целью в место возникновения несимметрии в расчетную схему вводится система из трех несимметричных напряжений, которая затем раскладывается на симметричные составляющие. Аналогично выражается через симметричные составляющие система трех несимметричных токов, создаваемых введенной системой несимметричных напряжений. В итоге несимметричную расчетную схему можно заменить тремя симметричными схемами, в каждой из которых действуют свои э. д. с., источники напряжения и токи. Различные элементы расчетной несимметричной схемы обладают сопротивлениями, определенными для каждой последовательности симметричных составляющих. Питающий трансформатор выдает симметричную систему э. д. с., поэтому э. д. с. источника учитывается только в схеме прямой последовательности. Для определения шести неизвестных векторных величин — симметричных составляющих тока и напряжения — достаточно составить шесть уравнений.
Рис. 4-5. Замыкание на корпус в трехфазной электроустановке, когда токами нагрузки можно пренебречь.
а — принципиальная схема; б — векторная диаграмма несимметричных токов и их составляющих.
Три уравнения составляются на основании трех схем для симметричных составляющих, а остальные три уравнения, исходя из граничных условий на том участке схемы, где создается несимметрия.
Применяем изложенный метод к расчету несимметричного режима в трехфазной сети, вызванного однофазным замыканием на корпус, если токами нагрузки можно пренебречь по сравнению с токами замыкания (рис. 4-5).
Применяем метод компенсации, включая в место замыкания систему трех напряжений
(рис. 4-6, а). Разложив на симметричные составляющие несимметричную систему напряжений и токов, можно составить три схемы для каждой последовательности. При этом считаем, что линия до места замыкания обладает сопротивлениями Ζ1, Ζ2 и Ζ0 для составляющих прямой, обратной и нулевой последовательностей. Составим эквивалентные схемы для прямой (рис. 4-6, б), обратной (рис. 4-6, в) и нулевой последовательностей (рис. 4-6, г). Для каждой из схем по 2-му закону Кирхгофа составим уравнение
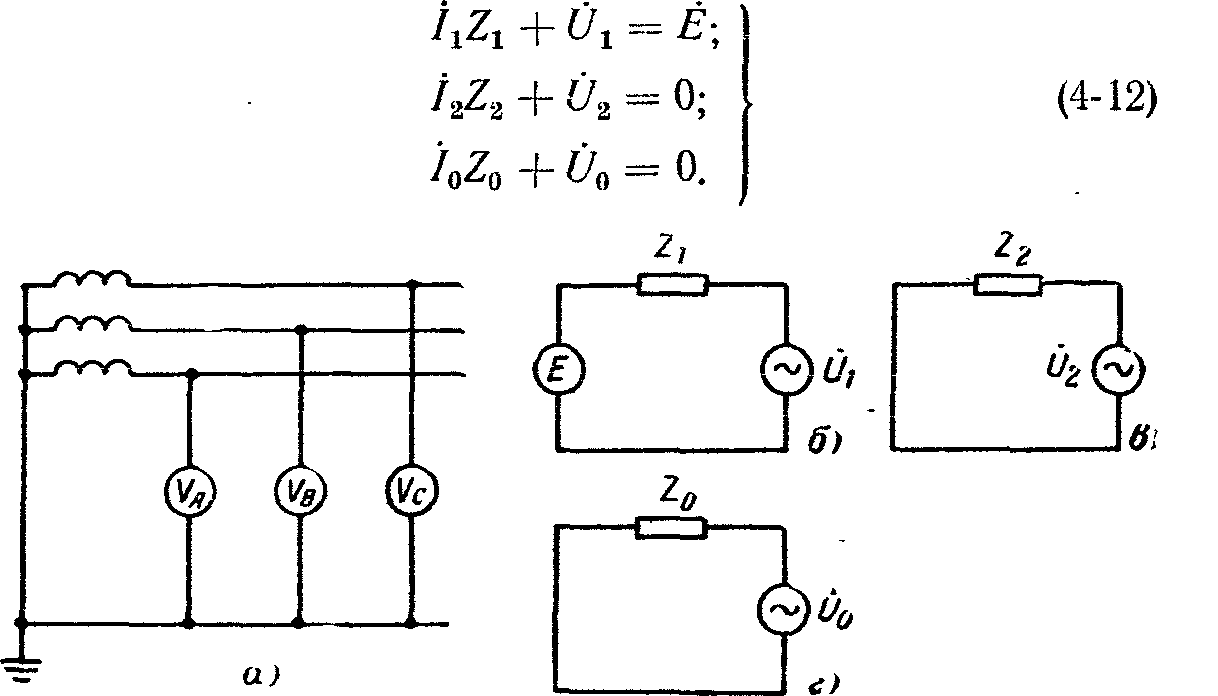
Рис. 4-6. Расчетная схема несимметричного (а) н эквивалентных симметричных (б, в, г) режимов однофазного замыкания.
Недостающие для определения симметричных составляющих тока и напряжения уравнения составляем из условий в месте замыкания:
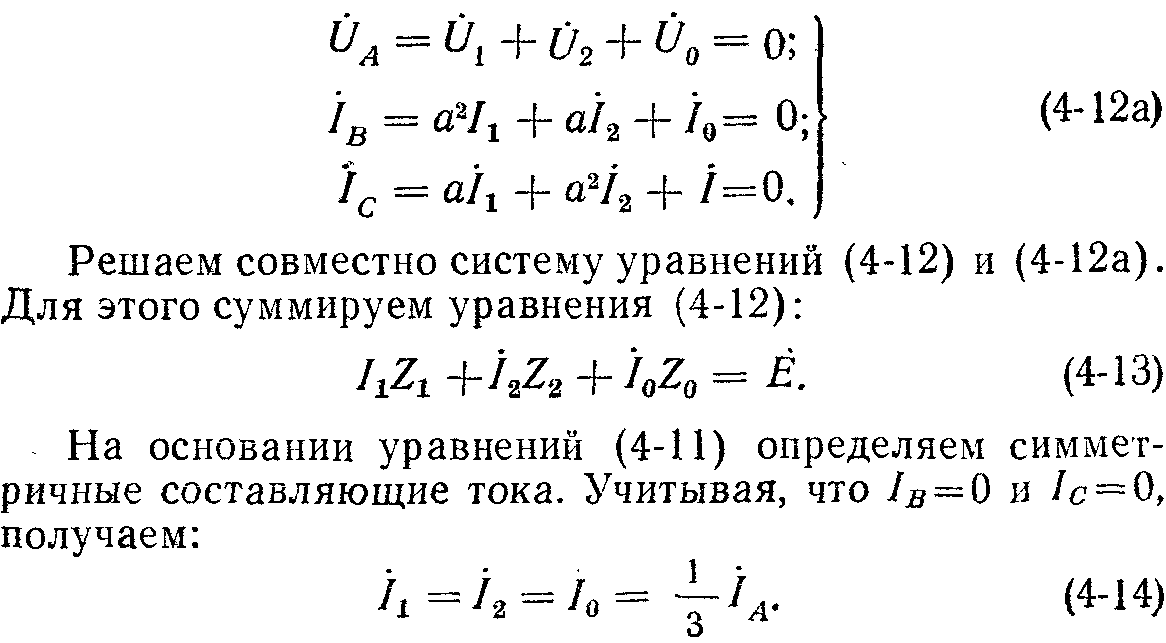
т. е. уравнение, вытекающее из закона Ома для однофазной схемы.
Таким образом, для расчета тока однофазного к. з. в трехфазной сети с малыми токами нагрузки можно применять расчетное выражение, полученное для однофазной схемы, если сопротивления элементов расчетной схемы для напряжений разных последовательностей одинаковы либо незначительно отличаются друг от друга. Применяющиеся в практике электроснабжения линии позволяют иногда принять
, однако у некоторых трансформаторов сопротивление нулевой последовательности резко отличается от сопротивлений прямой и обратной последовательностей, т. е.
Учитывая изложенное, выражение (4-15) можно представить в следующем виде:
Измерительный трансформатор тока учитывается активным и индуктивным сопротивлениями:
Коммутационный автоматический выключатель, если он применяется в расчетной схеме, учитывается активным и индуктивным сопротивлениями, которые принимаются одинаковыми для всех последовательностей:
Таким образом, полное сопротивление петли фазный — нулевой провод при точных расчетах должно определяться из соотношения
(4-19)
где rф, rн — активные сопротивления фазного провода и магистрали зануления для проводов из цветных металлов, равные омическому сопротивлению (при f=50 гц). Если магистраль зануления выполнена стальными проводниками, rн определяется по специальной методике (приводится ниже); х'— внутреннее индуктивное сопротивление магистрали зануления (учитывается только для стальных магистралей); х" — внешнее индуктивное сопротивление.
Активное и внутреннее индуктивное сопротивление стальных проводников нелинейно зависят от величины проходящего по ним тока, поэтому должны учитываться, исходя из величины расчетного тока замыкания по формуле (4-7). Для аналитического определения сопротивлений стальных проводников академиком Л. Р. Нейманом [Л. 25] предложены выражения
где I — длина стального проводника; Р — периметр проводника; γ — удельная электрическая проводимость стали; μ — магнитная проницаемость, определяемая из основной кривой намагничивания при напряженности поля, создаваемой расчетным током замыкания.
Рис. 4-7. Графики Л. Р. Неймана для расчета активного и внутреннего индуктивного сопротивлений стальных проводников.
Однако расчет по формулам (4-20) затруднен ввиду того, что не всегда представляется возможность воспользоваться кривой намагничивания для той стали, из которой изготовлен проводник. Поэтому Л. Р. Нейман упростил методику расчета и предложил графики, позволяющие определить r и х в зависимости от поверхностной плотности тока (отношения силы тока к периметру проводника). Из графика (рис. 4-7) в зависимости от отношения Ι/P находим:
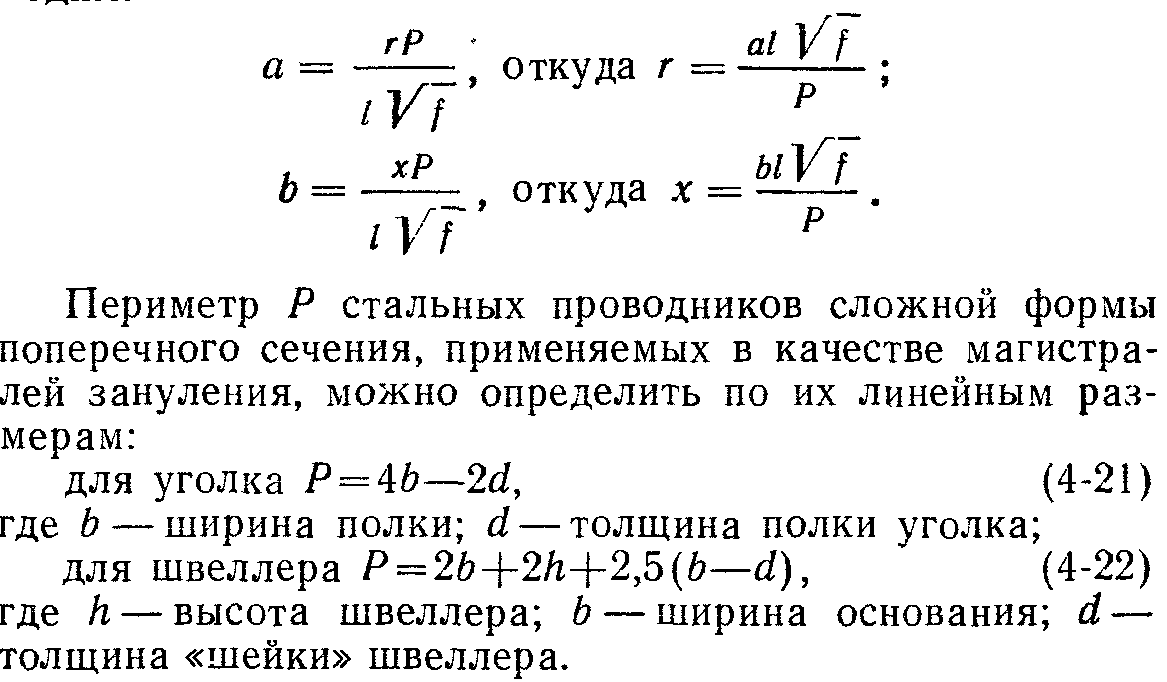
Для расчетов удобнее пользоваться табличными значениями сопротивлений стальных проводников. Активные и индуктивные сопротивления уголков и двутавровых балок, полученные экспериментально и приведенные к длине 1 км, даны в табл. 4-2 и 4-3 [Л. 26]. Сопротивления стальных проводников определяются в основном размерами их поверхности (в силу влияния поверхностного эффекта), поэтому в качестве магистралей зануления рекомендуется применять проводники из фасонной стали с более разветвленной поверхностью (с большим периметром). По этой же причине в отношении стальных проводников понятие «плотность тока» не характеризует их сопротивления.
Таблица 4-2
Активные и внутренние индуктивные сопротивления стальных уголков
Таблица 4-3
Активные и внутренние индуктивные сопротивления двутавровых балок
На основании данных табл. 4-2 были рассчитаны проводимости уголков, соответствующие 50% проводимости фазного провода.
При этом проводимости стальных уголков принимались для тока замыкания, равного 300 А. При больших значениях токов проводимости уголков, выбранные по табл. 4-2, будут удовлетворять требованиям расчета с запасом.
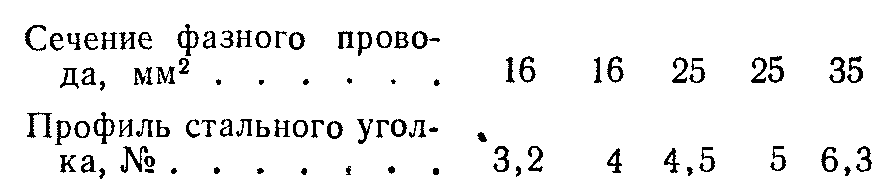
Следует отметить, что стальные проводники экономически нецелесообразно использовать при длине магистралей зануления, превышающей 50 м. Их можно рекомендовать также к применению в качестве ответвлений к электрооборудованию, когда существенную роль начинает играть их повышенная механическая прочность. Во всех остальных случаях проводимость стальных проводников в схемах зануления целесообразно учитывать, если они используются по основному назначению для каких- либо технологических нужд.
Внешнее индуктивное сопротивление х" учитывают приближенно величиной 0,6 Ом/км [Л. 9]. Однако при точном расчете проводимости цепи к. з. по (4-19) такой подход может внести существенную погрешность и учет незначительных сопротивлений (автоматического выключателя, электрической дуги и т. п.). теряет смысл. Поэтому при точных расчетах рекомендуется рассчитывать внешнее индуктивное сопротивление.
Если петля фазный — нулевой провод выполнена из круглых проводников различного радиуса (наиболее частый вариант схемы зануления), внешнее индуктивное сопротивление (Ом/км) предлагается рассчитывать по выражению [Л. 27]
Очевидно, что внешнее индуктивное сопротивление резко возрастает с увеличением расстояния между фазным проводом и магистралью зануления (нулевым проводом). По этой причине магистрали зануления размещают возможно ближе к фазным проводам.
Приведенная методика позволяет рассчитывать ток однофазного к. з. в однофазных схемах и в трехфазных схемах, когда мощность нагрузки, подключенной к аварийной линии, незначительна по сравнению с мощностью питающего трансформатора, т. е. когда токами нагрузки можно пренебрегать по сравнению с токами к. з. на корпус. Остановимся на некоторых частных случаях расчета такого рода схем при специфических электропроводках.