2.3. Экспериментальные исследования теплообмена на турбинных профилях и их обобщения.
Ввиду сложности теплообмена на поверхности турбинных профилей важное значение приобретает его непосредственное экспериментальное изучение. Как показывают детальные измерения, распределение величины коэффициента теплоотдачи а по поверхности профиля имеет достаточно сложную картину, является весьма неравномерным и в сильной степени подвержено изменениям в зависимости от режима течения. В качестве примера можно указать экспериментальные работы Вильсона, Поупа [145], Уолкера, Мэркланда [143], Тернера [141], М.Н. Бодунова [11] и др. Прямые измерения показывают, что величина коэффициента теплоотдачи на профиле изменяется в широких пределах, имея локальный максимум у передней кромки лопатки, достаточно сильное возрастание интенсивности теплоотдачи происходит в области перехода от ламинарного к турбулентному режиму течения (при турбулентном режиме течения в пограничном слое уровень значений коэффициента теплоотдачи а выше, чем в зоне ламинарного режима). Резкое возрастание коэффициента теплоотдачи происходит также в месте возникновения отрывного течения. Классическая картина распределения коэффициента теплоотдачи на профиле получена Вильсоном и Поупом [145] . Опыты проводились при обтекании профиля спокойным потоком (с весьма низкой степенью турбулентности Ти< 1%), опытное распределение коэффициента теплоотдачи на выпуклой стороне экспериментального профиля показано на рис. 2.5 (опытным точкам, ●,Δ, О и расчетным кривым 1, 2, 3 соответствуют числа Рейнольдса Re2 = 1,84-105; 3,02· 105; 6,75· 105; ).
Данные представлены в виде зависимости величины Nu√Re2 от х/су где Nu — число Нуссельта![]() — число Рейнольдса, определенное по параметрам на выходе из решетки; эти параметры снабжены индексом «2», с — длина хорды лопатки.
— число Рейнольдса, определенное по параметрам на выходе из решетки; эти параметры снабжены индексом «2», с — длина хорды лопатки.
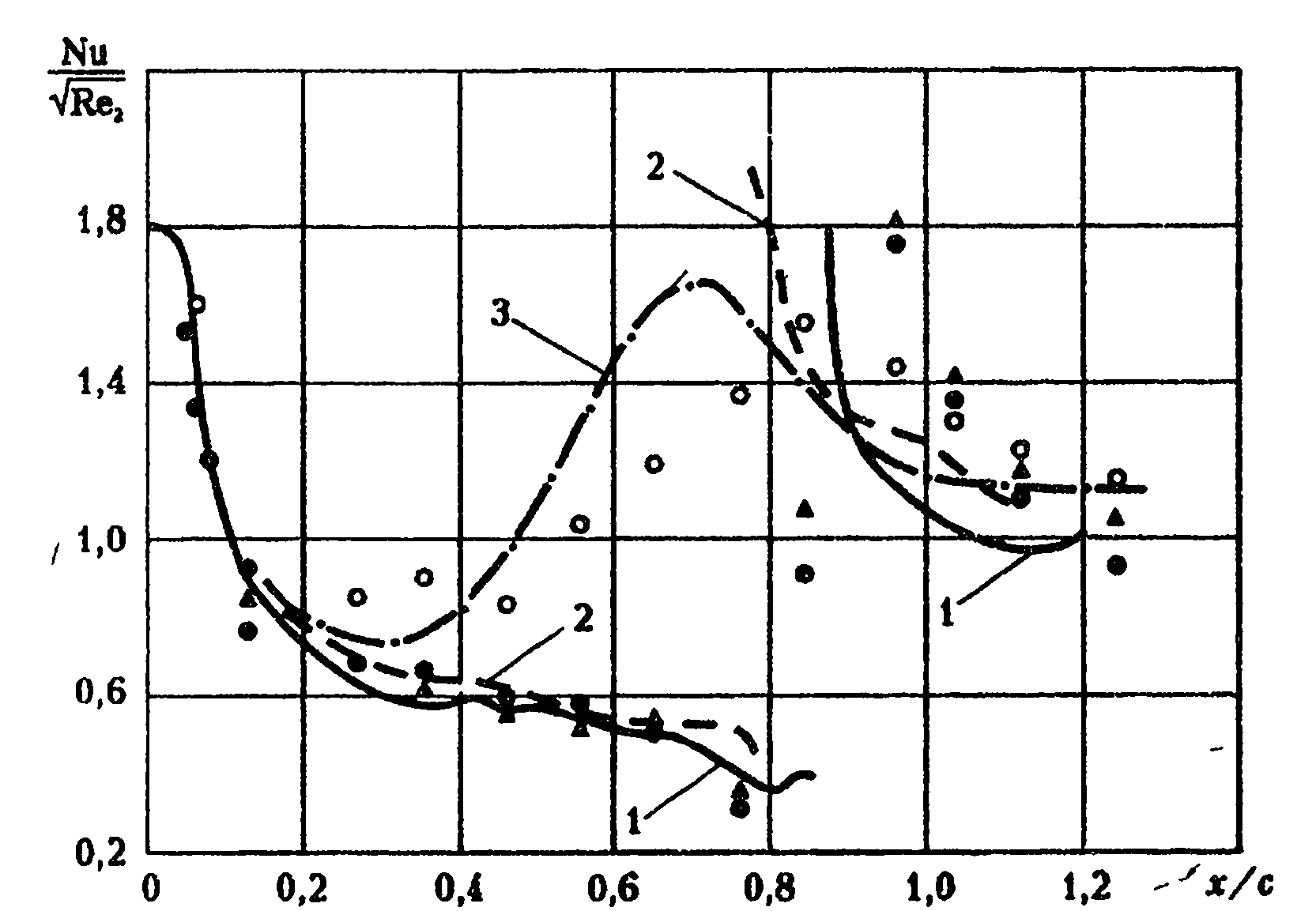
Рис. 2.5. Распределение коэффициента теплоотдачи по профилю лопатки
Величины р и μ в опытах были постоянными. При меньших значениях числа Рейнольдса (Rе2= 1,84-105 и Re2= 3,02· 105) режим течения в пограничном слое оставался ламинарным, фактически до х/с =0,8 (х — расстояние вдоль контура от критической точки), где, согласно указанию авторов работы [145], происходил отрыв пограничного слоя. Именно этим объясняется резкое (практически скачком) возрастание значения коэффициента теплоотдачи, что еще раз подчеркивает огромное влияние отрывов на локальные значения коэффициентов теплоотдачи. Возникновение отрыва в данной ситуации объясняется неблагоприятным распределением скорости внешнего течения (вне пограничного слоя в области х/с- 0,75-0,9 скорость ие(х) убывает, что соответствует положительному градиенту давления). В случае существенно большего числа Рейнольдса Re2 = 6,75 -105 изменение коэффициента теплоотдачи по профилю более плавно, непрерывное возрастание его на участке от х/с = 0,4 до 0,85 вполне логично объясняется переходом от ламинарного режима течения в пограничном слое к турбулентному. К месту неблагоприятного распределения внешней скорости режим течения в пограничном слое становится развитым турбулентным. В этом случае в эксперименте отрыв пограничного слоя не наблюдался, что соответствует известным фактам, согласно которым турбулентный режим течения более устойчив к отрыву, чем ламинарный.
На рис.2.5 показаны результаты измерения при угле натекания β= 30°. Данные режимы отличались только числом Рейнольдса Re2, но уже этого оказалось достаточным, чтобы изменение распределения коэффициента теплоотдачи по профилю было весьма существенным.
Пояснение расчетных кривых по методу [61] на рис. 2.5 приведено на стр. 98.
Работа [143] является развитием исследований [145] и посвящена экспериментальному изучению влияния вторичных течений на теплообмен у турбинных профилей (в опытах отмечается увеличение теплообмена за счет вторичных течений).
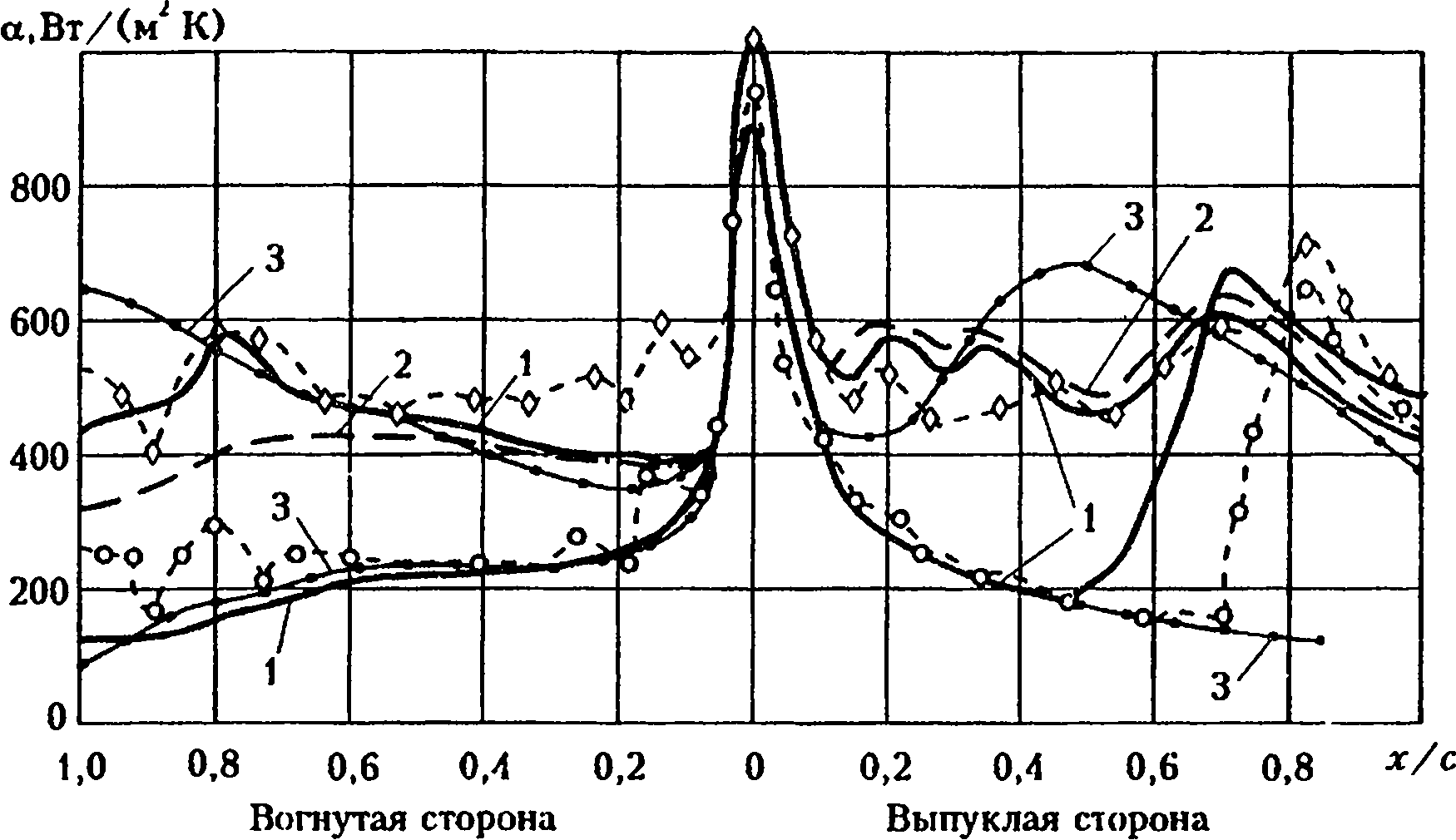
Рис. 2.6. Распределение коэффициентов теплоотдачи по профилю лопатки при различной внешней турбулентности:
1 — расчеты с учетом кривизны [61], 2 — расчеты без учета кривизны,
3 — расчеты Макдональда, Фиша [132]
Повышение степени турбулентности внешнего потока приводит к существенному изменению уровня и распределения теплоотдачи по поверхности профиля. В качестве примера (рис. 2.6) рассмотрим результаты измерений Тернера [141] (О -- при низкой (Тu =0,45 % ) и О — высокой (Тu = 5,9%) степенях турбулентности набегающего потока на входе в межлопаточный канал). При низкой степени турбулентности на выпуклой стороне профиля наблюдается область ламинарного пограничного слоя, перехода и турбулентной зоны (картина в значительной степени похожа на результаты работы [145]), на вогнутой стороне профиля быстро снижается теплообмен при удалении от передней критической точки профиля, затем его величины сохраняются примерно на одном уровне, соответствующем теплоотдаче на выпуклой стороне при ламинарном режиме. Увеличение степени турбулентности набегающего потока до Ти = 5,9 % приводит к существенному возрастанию теплоотдачи в среднем на обеих сторонах профиля, а также в области его передней кромки. Пояснение расчетных кривых 1, 2 приводится далее (стр. 98), кривые 1, 2 получены с использованием метода [61].
Существенное влияние степени турбулентности набегающего потока на теплоотдачу у турбинных профилей получено также в экспериментальных работах В.М. Капиноса, А.Ф. Слитенко, В.Б. Титова [34], Даниельса, Брауна [120], Консиньи, Ричардса [36]. В этих работах отмечается влияние Тu на положение перехода от ламинарного к турбулентному режиму течения, исследуется влияние на теплопередачу и других параметров; например, в работе [36], изучалось влияние угла входа, числа Маха на входе, числа Рейнольдса. В работе [34] представлено распределение локальных значений степени турбулентности внешнего потока по профилю лопатки, показано, что Тu существенно изменяется вдоль профиля (в опытах Тu вдоль профиля изменяется более, чем на порядок).
Очень сильное влияние на распределение коэффициента теплоотдачи могут также оказывать резкие изменения граничных условий: продольная неизотермичность, наличие участков вдува, резкого разгона или торможения потока вне пограничного слоя и т.д. Об этом свидетельствуют опытные данные Моретти, Кейса [133], Симеона [139] и др.
Экспериментальные исследования по определению коэффициентов теплоотдачи и получению эмпирических зависимостей ведутся давно. Эмпирические зависимости, как правило, имеют частный характер и получены, в основном, для средних коэффициентов теплоотдачи (осреднение производится по определенному участку поверхности профиля, например по области у передней кромки, у задней кромки, в срединной части профиля). Естественно, эмпирические зависимости могут быть использованы лишь в том диапазоне изменения параметров, в котором проводились эксперименты; поэтому их применение достаточно ограничено. Следует обратить внимание на то, что данные о средних коэффициентах теплоотдачи обладают существенно меньшей информацией, чем о локальных коэффициентах теплоотдачи. И в ряде случаев данные о средних коэффициентах теплоотдачи могут оказаться недостаточными для определения с требуемой точностью картины теплового состояния профиля.
Укажем здесь некоторые эмпирические зависимости для средних коэффициентов теплоотдачи, применяемые в оценочных расчетах. При расчете среднего коэффициента теплоотдачи в области входной кромки используется критериальное равенство, полученное осреднением в окрестности передней критической точки опытных данных Г.Н. Кружилина, В.А. Шваба (1935 г.) по коэффициенту теплоотдачи на цилиндре:
![]()
(2.23)
где числа Нуссельта![]() и Рейнольдса
и Рейнольдса![]()
определяются по параметрам на входе в решетку; авх — среднее значение коэффициента теплоотдачи в области входной кромки (осреднение произведено по длине дуги в пределах угла ± 70- 75° от передней критической точки); d1— диаметр вписанного цилиндра у входной кромки; λ— теплофизические свойства газа на входе в решетку; и1 — скорость на входе в решетку в случае сопловой лопатки, для рабочей лопатки это скорость в относительном движении на входе в решетку. Формулу (2.23) рекомендуется использовать при дозвуковых скоростях, нулевых углах входа, низкой степени турбулентности в диапазоне Re1= 2,8· 103- 2,8 - 104.
Некоторые результаты расчетов локальных коэффициентов теплоотдачи на профилях и их сопоставление с опытными данными.
С помощью изложенного метода были проведены многочисленные расчеты пограничных слоев при различных граничных условиях.
Наибольший интерес представляют расчеты теплоотдачи на турбинных профилях. На рис. 2.5 кривыми показаны результаты расчета теплоотдачи к выпуклой стороне профиля, локальные коэффициенты теплоотдачи к которому измерены в работе Вильсона, Поупа [145] (расчетные линии 1,2,3 соответствуют Re2= 1,84· 105 ; 3,02· 105 ; 6,75-105). При наименьшем в опытах числе Re2 = 1,84· 10 , определенном по параметрам на выходе из решетки, в расчетах получается отрыв, местоположение которого совпадает с указанным в опытах. При наибольшем числе Re2= 6,75-10 отрыв не наблюдается, в этом случае пограничный
слой в месте неблагоприятного градиента давления оказывается уже турбулентным, а турбулентный пограничный слой более устойчив к отрыву, чем ламинарный (отрыв отсутствует и в эксперименте). Некоторое количественное отличие расчета от опыта по теплоотдаче в случае безотрывного течения наблюдается в переходной области. При возникновении отрыва дальнейший расчет в зоне за отрывом проводился в предположении, что в месте отрыва происходит резкий переход к турбулентному режиму течения. Это предположение позволило получить качественное согласование расчетов с опытами в области за отрывом, хотя определенное количественное различие наблюдается. Внешнее распределение скорости здесь взято из эксперимента (т.е. с учетом отрыва, если он есть). Степень турбулентности в этом случае мала.
Расчеты теплоотдачи к лопаткам при более высокой степени турбулентности проведены в соответствии с исходными данными экспериментальной работы Тернера [141] для значений Тu= 0,45% и Тu= 5,9% (параметры торможения Т* = 369 К, р* = 1,53· 105 Па, параметры на выходе из решетки М2 = 0,75 , Re2= 1,05· 10 ). Результаты расчета распределения локального коэффициента теплоотдачи по профилю показаны на рис. 2.6. Расчетные данные, полученные с учетом степени турбулентности и продольной кривизны профиля удовлетворительно согласуются с опытными (сплошные линии). Результаты свидетельствуют о существенном влиянии степени турбулентности на теплоотдачу. При низкой степени турбулентности наблюдаются протяженные участки ламинарного режима (практически на всей вогнутой стороне и на выпуклой до х/с= 0,6, с — хорда). При степени турбулентности Тu= 5,9% протяженную зону занимает переходный режим течения (коэффициенты переноса имеют промежуточные значения между молекулярными и молярными); при этом в целом уровень теплообмена существенно возрастает.
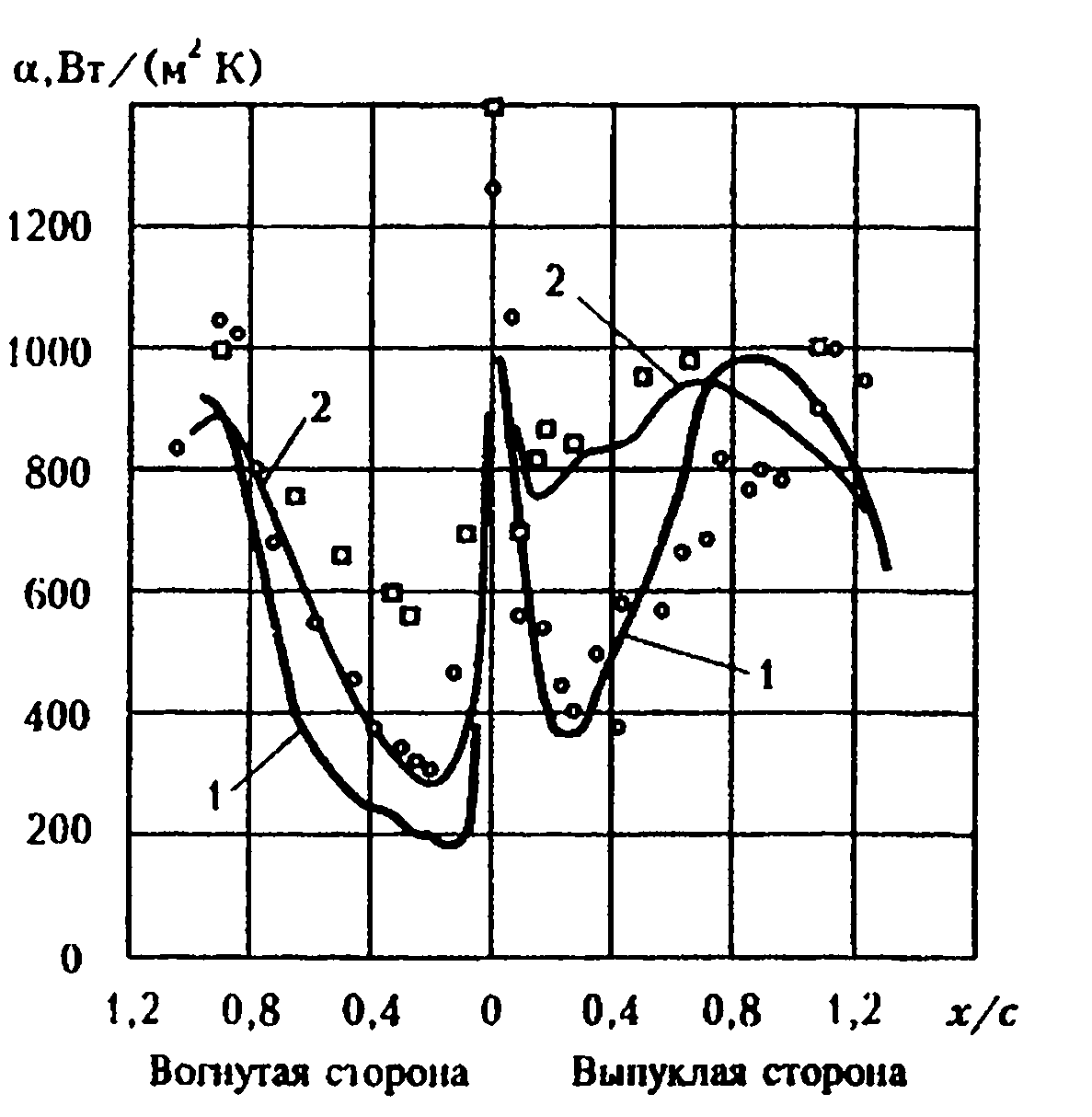
Рис. 2.12. Распределение коэффициента теплоотдачи по профилю лопатки при различных степенях турбулентности
Расчет без учета продольной кривизны показан штрих-пунктирной линией. Учет кривизны является существенным в переходной и турбулентной областях и заметно улучшает соответствие между расчетными и опытными данными (особенно это заметно на вогнутой стороне профиля).
Еще один пример расчета теплоотдачи к профилю по методу [61] при различных степенях турбулентности внешнего потока показан на рис. 2.12. В качестве исходных здесь использованы данные из работы Консиньи, Ричардса [36] по измерению теплоотдачи к лопаткам турбины.
Опыты проводились при Тu= 0,8% (1) и Тu= 5,2% (2) и параметрах потока M2 = 0,92 , β=45°,
р* = 2,348· 105 Па, T* = 417 К, Tw= 290 К . Здесь также заметно сильное влияние степени турбулентности на теплообмен. Показанные на рис. 2.12 расчетные кривые 1 и опытные точки (О) соответствуют Тu= 0,8%, кривые 2 и опытные точки (□) соответствуют Тu= 5,2%. На выпуклой стороне профиля расчет качественно и количественно находится в соответствии с опытами. Заметное отличие между расчетом и опытами на вогнутой стороне профиля объясняется тем обстоятельством, что расчет в этом случае проводился без учета продольной кривизны профиля. Заметим также, что на вогнутой стороне профиля возникает локальный отрыв.
Результаты расчета теплового потока к профилю лопатки плоской решетки, исследованной экспериментально в работе Даниельса, Брауна [120] (точки), показаны на рис. 2.13 (s — длина криволинейного контура на выпуклой или вогнутой сторонах). Опыты проводились при низкой степени турбулентности и параметрах потока Мх = 0,38, β1 = 48°, р*= 0,19 МПа, Т* = 432 К, Tw= 289 К. Результаты расчетов по настоящей методике [61] (сплошная линия находятся в хорошем соответствии с опытами для выпуклой и, для вогнутой сторон профиля. На рис. 2.13 демонстрируются также результаты расчетов по другим методам, в частности с использованием многопараметрических моделей. На рис. 2.13 показаны расчеты по программам Себечи — Смита (штрих-пунктирная линия 2), Патанкара — Сполдинга (мелкий пунктир 3), Уилкокса (линия 4 в виде точек), модифицированной программе Уилкокса с уточненным табличным заданием Ргт (крупный пунктир 5).
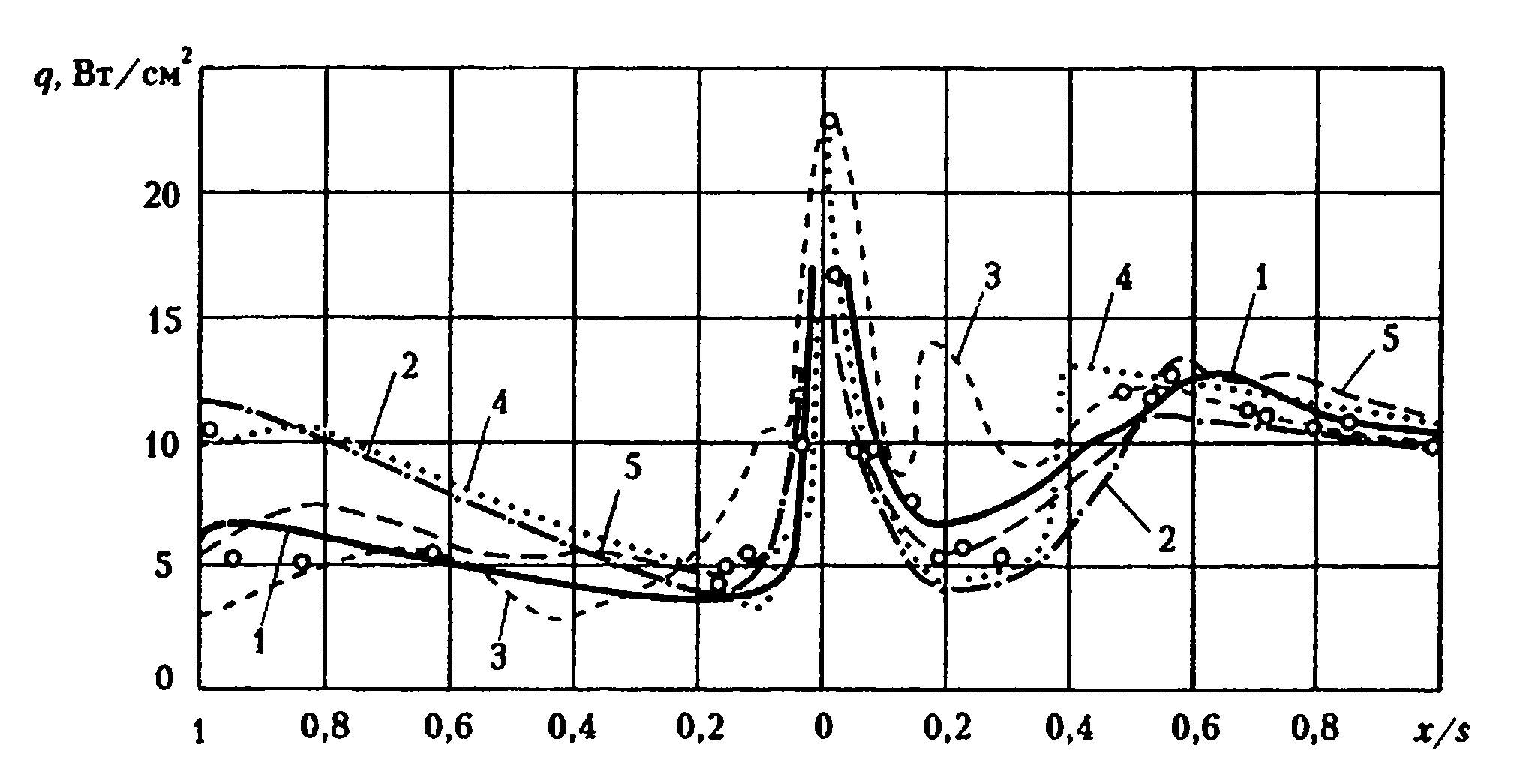
Рис. 2.13. Распределение теплового потока по профилю рабочей лопатки
Из сравнения всех расчетных данных на рис. 2.13 с опытами видно, что настоящий метод не уступает по точности другим методам. Также можно заключить, что использование более сложных многопараметрических моделей турбулентности не имеет заметных преимуществ по сравнению с используемой здесь моделью коэффициентов полного переноса.
Расчеты по вышеизложенному методу, результаты которых показаны на рис.* 2.12, 2.13, выполнены С.П. Чиковой; она дополнила метод итерациями по δ*, что позволило учесть влияние толщины вытеснения на внешнее течение, а также малые зоны отрыва.
Влияние неизотермичности поверхности на теплоотдачу. Рассмотрим теплоотдачу к пластине, которая содержит участок (от Rex 10 = 0,35 до 0,75) линейного изменения температуры стенки [80]. Пусть температурный фактор (t= Tw/Te) в начале указанного участка tH= 0,5, , а в конце участка он достигает величины tK , которая принимает следующие значения tK = 0,25; 0,5; 0,75;
1. Вне указанного участка температурный фактор постоянен. Рассмотрим также вариант, когда температурный фактор постоянен на всей пластине и равен t= 0,75 .
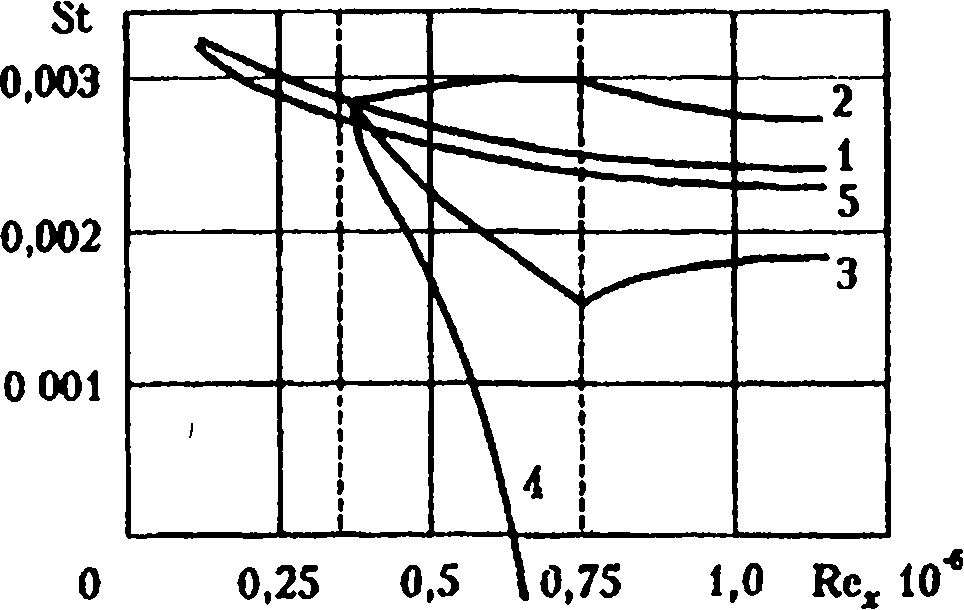
Рис. 2.14. Изменение числа Стантона на неизотермической поверхности
Примем М = 0,2 . Расчеты показывают, что число Стантона изменяется на участке неизотермичности в несколько раз, и даже может изменять знак, что свидетельствует о возникновении противоположного по знаку теплового потока у стенки.
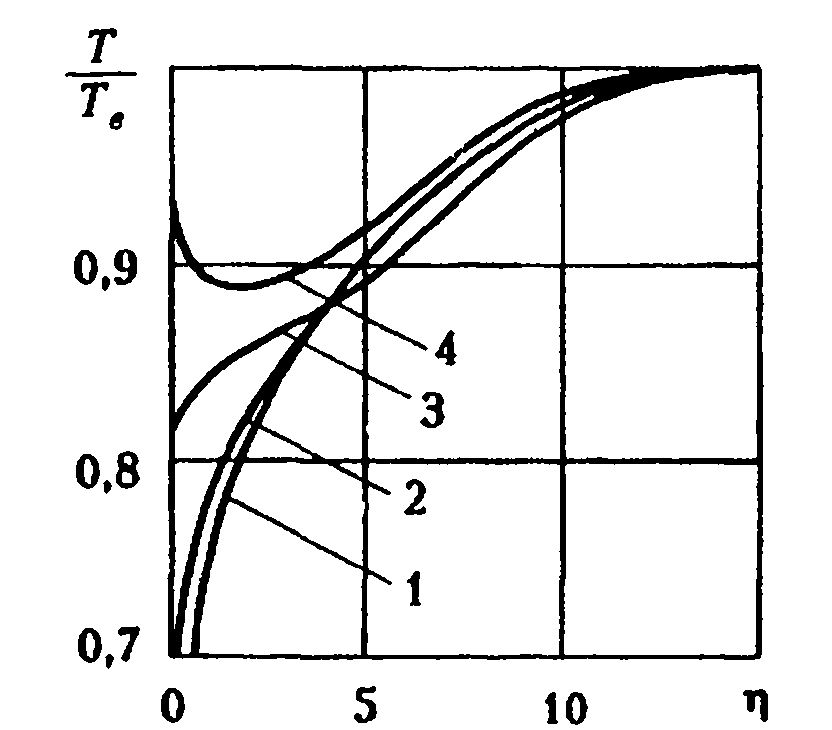
Рис. 2.15. Температурные профили на неизотермическом участке пластины
Расчетные кривые 1—4 на рис. 2.14 соответствуют tK = 0,25; 0,5; 0,75; 1; кривая 5 получена при постоянном температурном факторе 0,75. Из расчетов следует, что теплоотдача существенно уменьшается, если температура стенки возрастает в направлении течения. Если температура стенки убывает, эффект противоположный.
Кривые 1 и 5, рассчитанные при постоянных температурных факторах, соответственно равных t= 0,5 и 0,75, указывают на слабую зависимость теплоотдачи от постоянного температурного фактора. Столь существенная зависимость числа Стантона от продольной неизотермичности объясняется деформацией профилей температуры на участке неизотермичности.
На рис. 2.15 показаны профили температуры на участке неизотермичности 0,5< t< 1, причем кривые 1—4 вычислены соответственно при различных Rex и t (Rex· 10-5 = 4; 5;6; 7; и Tw/Te = 0,5625; 0,6875; 0,8125; 0,9375).
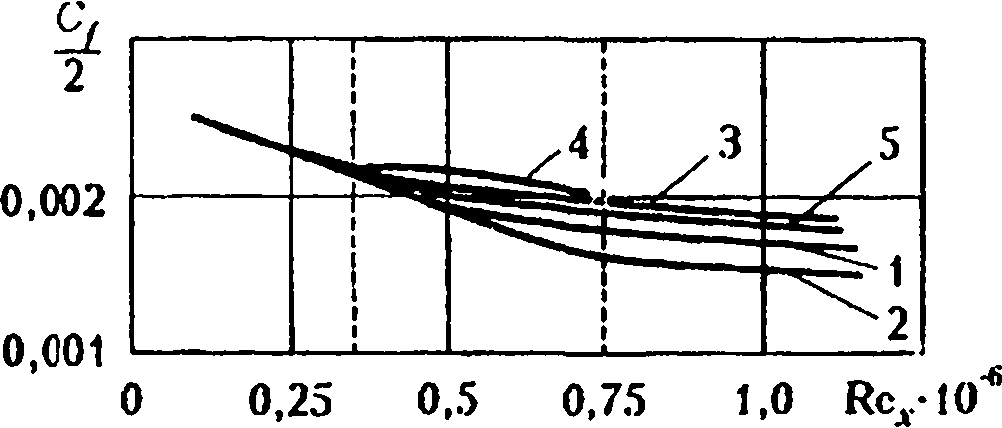
Рис. 2.16. Изменение коэффициента трения на неизотермической поверхности
В соответствии с кривой 4 направление теплового потока действительно изменилось. Коэффициент трения также зависит от неизотермичности поверхности (рис. 2.16), однако эта зависимость существенно более
слабая (кривая 1 — Tw/Te= 0,5; кривая 2 — Tw/Te = 0,5 + 0,25; кривая 3 — Tw/Te= 0,5 + 0,75; кривая 4 — Tw/Te- 0,54-1; кривая 5 — Tw/Te= 0,75). Таким образом, учет неизотермичности поверхности профиля необходим, особенно на охлаждаемых турбинных профилях, где эта неизотермичность особо существенна.

