Тепловая защита лопаток турбин - Моделирование турбулентных течений

До настоящего времени не разработана рациональная теория турбулентного вида движения, которая позволила бы получить уравнения, описывающие процессы турбулентного переноса. При турбулентном движении на основное течение накладывается достаточно интенсивное дополнительное, характеризующееся сильной нестационарностью. Замечено, что турбулентный режим течения реализуется при достаточно больших числах Рейнольдса Re. В настоящее время имеется огромное количество публикаций, посвященных моделированию турбулентных течений, что, очевидно, одновременно свидетельствует и о большом интересе к проблеме, и о неудовлетворенности уже имеющимися результатами. Собран также большой экспериментальный материал, который в значительной степени нуждается в дальнейшем обобщении и глубоком осмыслении.
В теоретическом плане представляется естественным использовать для описания турбулентных движений уравнения Навье — Стокса, решения которых весьма хорошо соответствуют реальным течениям при достаточно малых числах Re в случае ламинарного режима. Однако с ростом числа Re ламинарный режим течения переходит в турбулентный, решения уравнений Навье — Стокса становятся неустойчивыми, а известные точные решения этих уравнений перестают описывать течения при больших числах Рейнольдса (т.е. задача, использующая уравнения Навье — Стокса при больших числах Re, приобретает черты некорректно поставленной).
Существуют концепции, согласно которым турбулентная форма движения жидкостей не описывается уравнениями Навье -Стокса. Таким примером могут служить работы В.В. Струминского. В то же время весьма интересные результаты, подтверждающие правомерность использования уравнений Навье Стокса при достаточно больших числах Рейнольдса, были получены Б.Л. Рождественским с сотрудниками. В результате численных расчетов непосредственно уравнений Навье — Стокса удалось получить виды течения, напоминающие турбулентные образования.
Для теоретического описания турбулентных движений обычно используется процедура осреднения уравнений Навье — Стокса и получения системы уравнений Рейнольдса, описывающей осредненное турбулентное движение.
При операции осреднения все величины, содержащиеся в исходных уравнениях, представляются в виде суммы осредненной и пульсационной составляющих, т.е.

Операция осреднения обозначена здесь чертой. Очевидно,
Если применить осреднение к уравнениям Навье — Стокса, то в уравнениях движения появляются дополнительные члены, которые получены в результате осреднения произведений пульсационных составляющих скорости. Их обычно называют кажущимися напряжениями или напряжениями Рейнольдса и включают в качестве дополнительных слагаемых в компоненты тензора напряжений, которые представляются в виде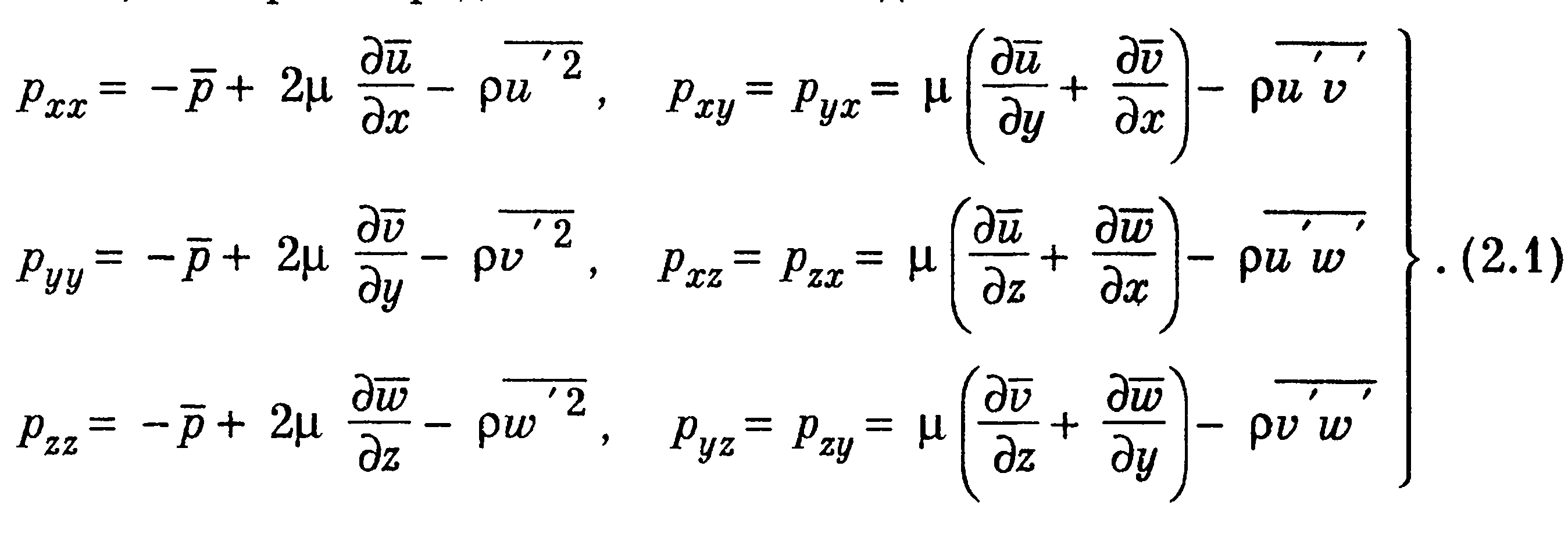
Здесь х ,у ,ζ — координаты;  v ,w — составляющие вектора скорости; р — статическое давление; р — плотность; μ — коэффициент динамической вязкости. Напряжения Рейнольдса являются неизвестными функциями. С их введением число неизвестных превышает число уравнений, поэтому для замыкания системы уравнений необходимы дополнительные сведения о кажущихся напряжениях. В приближениях теории пограничного слоя система уравнений неразрывности и движения с учетом (2.1) в случае установившегося осредненного движения несжимаемой жидкости принимает вид

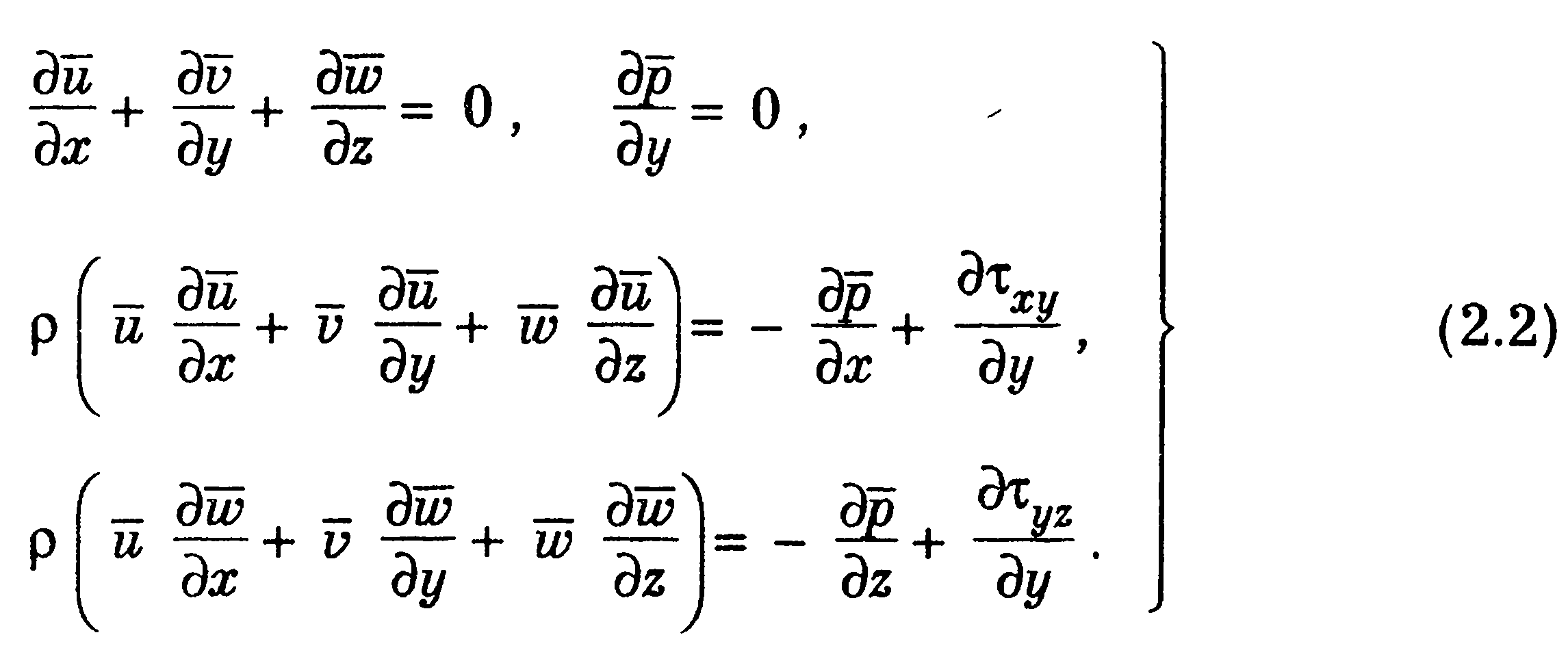
Здесь—напряжения трения, содержащие слагаемые, обусловленные молекулярной вязкостью и турбулентным перемешиванием. Одной из первых гипотез турбулентности является гипотеза Буссинеска, согласно которой турбулентные составляющие напряжений представляются в виде

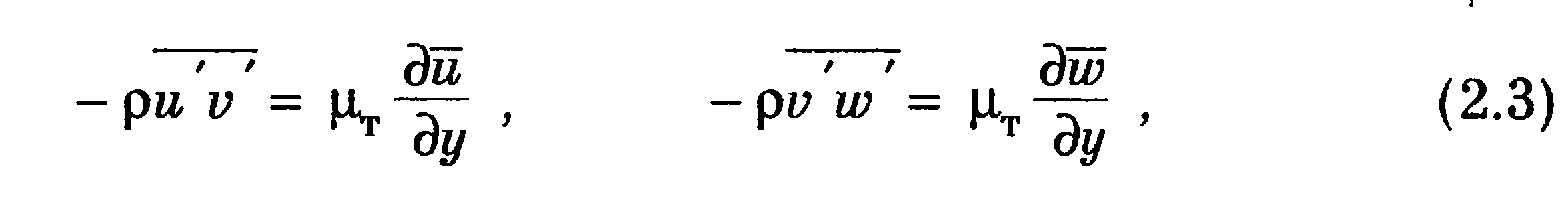
где μτ называют коэффициентом турбулентной вязкости. Формулы (2.3) приняты по аналогии с законом Стокса для ламинарного режима течения. В настоящее время они вызывают многочисленные критические замечания, в частности, это связано с тем, что согласно формулам (2.3) трение и градиент средней скорости должны быть равны нулю одновременно, что во многих случаях противоречит известным опытным данным. Содержащийся в выражениях (2.3) коэффициент турбулентной вязкости μτ не является свойством жидкости, а определяется характером течения; установление аналитического выражения для коэффициента μτ требует дополнительных гипотез.
Приведем также систему уравнений многокомпонентного сжимаемого турбулентного пограничного слоя в случае установившегося осредненного движения. Уравнения неразрывности, движения, диффузии i-το компонента и энергии представляются в виде (здесь и в дальнейшем опускаем черточки над осредненными величинами)

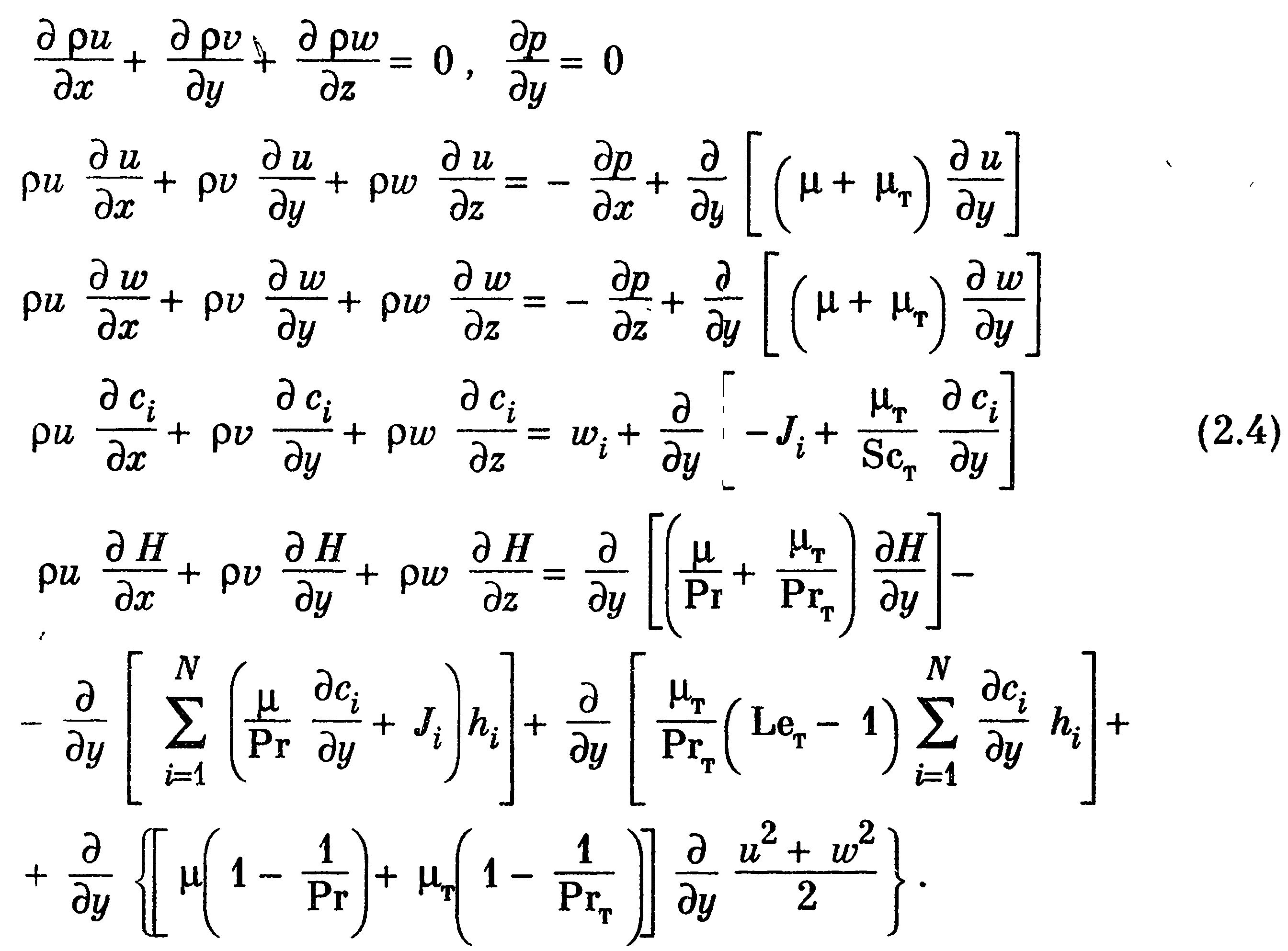
Здесь с·, /· — массовая концентрация и диффузионный поток i—то компонента; wi — плотность источника массы i-το компонента; Н — полная энтальпия смеси; hi— теплосодержание i-гο компонента;
При выводе системы (2.4) сделано дополнительное предположение о возможности пренебрежения членами, связанными с осреднением пульсаций плотности и коэффициентов молекулярного переноса. Здесь по аналогии с гипотезой Буссинеска введены кроме коэффициента турбулентной вязкости μτ , также коэффициенты турбулентной диффузии Ζ>τ, которые полагаются одинаковыми для всех компонентов смеси, и турбулентной теплопроводности λτ; в уравнениях (2.4) также содержатся числа Прандтля, определенные по молекулярным и молярным (турбулентным) коэффициентам переноса, а также числа Шмидта и Льюиса, определенные по коэффициентам турбулентного переноса. Уравнение энергии в системе записано в пренебрежении эффектами баро- и термодиффузии и при постоянных удельных теплоемкостях отдельных компонентов. Каждая из приведенных здесь систем уравнений (2.2) и является незамкнутой. В системе (2.4) неизвестны коэффициенты турбулентного переноса μτ, DT, λτ .
Проблема замыкания системы уравнений Рейнольдса привлекала внимание крупнейших исследователей (Фридмана, Колмогорова, Прандтля, Кармана). В 20—30-е годы предпринимались попытки получить замкнутую систему уравнений турбулентного движения посредством вывода цепочки уравнений, содержащих корреляционные моменты более высокого порядка. Однако попытки таким образом вывести замкнутую систему (на уровне получения точных уравнений) не привели к успеху. Предлагались некоторые гипотезы, например М.Д. Миллионщиковым, устанавливающие связь между моментами различного порядка; к данному направлению относятся развиваемые в настоящее время методы инвариантного моделирования. Наиболее значительные успехи в моделировании турбулентных течений были достигнуты в работах Прандтля, Кармана, Тейлора. В настоящее время среди большого количества моделей турбулентности можно выделить две наиболее характерные группы. К первой группе отнесем модели, устанавливающие конечные связи между различными характеристиками турбулентности. Вторая группа включает более сложные модели турбулентности, использующие дополнительные дифференциальные уравнения для некоторых характеристик турбулентности (обзор моделей турбулентности приведен, например в [45]).
Вначале рассмотрим некоторые модели турбулентности первой группы. Весьма широкое распространение получила гипотеза Прандтля (1925 г.), согласно которой устанавливаются следующие формулы для турбулентной вязкости и трения в пристеночной области:

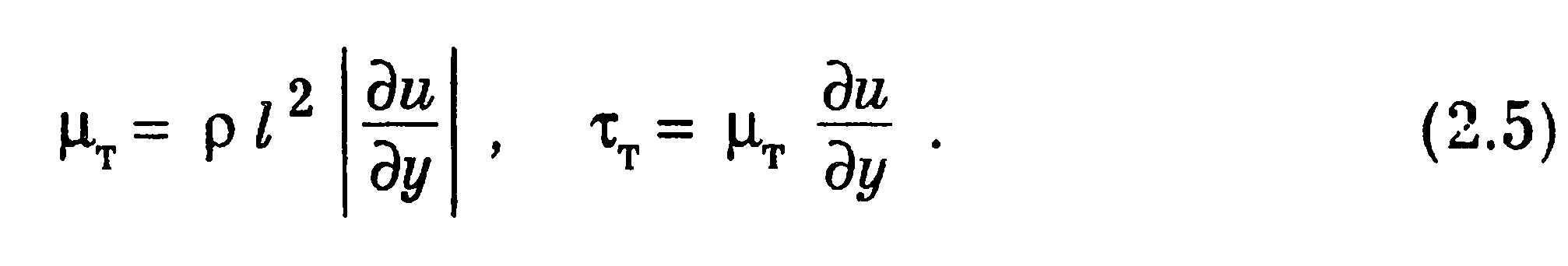
Здесь I — масштаб турбулентности, называемый длиной пути перемешивания. Длина пути перемешивания понимается как некоторое расстояние, при прохождении которого турбулентный моль (комок жидкости) полностью перемешивается с окружающими его молями, теряя свою индивидуальность. Принято, что около стенки эта величина определяется формулой
1= ку,                                                                                            (2.6)
где к — константа турбулентности Кармана (к= 0,4). Если использовать гипотезу Прандтля для расчета течения несжимаемой жидкости в пристеночной области у пластины, то получается логарифмический профиль скорости
(2.7)
где(v* — динамическая скорость, v — коэффициент кинематической вязкости). Поскольку полученный профиль скорости (2.7) не удовлетворяет условию прилипания на стенке, то возникает необходимость рассмотрения ламинарного подслоя (тонкого слоя у стенки, где течение ламинарное), для которого из уравнения движения следует
(2.8)
Таким образом, в пристеночной области может рассматриваться двухслойная схема: ламинарный подслой — турбулентное ядро. Профиль скорости в этом случае получается составным (2.7). Переход от ламинарного подслоя к турбулентному ядру в этой схеме осуществляется скачком на границе ламинарного подслоя, которой соответствует η = ηκ (из опытов ηκ~ 10+ 12). Нетрудно видеть, чтоявляется некоторым критическим числом Рейнольдса, определенным на границе ламинарного подслоя. Критическое значение ηκ относят к константам турбулентности. На внешней стороне пограничного слоя профиль скорости также отличается от логарифмического. В рамках двухслойной схемы могут также рассматриваться процессы теплообмена, диффузии.

Имеются многочисленные модели, уточняющие двухслойную схему. Одной из первых попыток такого рода было введение «буферного» слоя, в котором одновременно учитываются механизмы молекулярного и турбулентного переносов.
Для понимания сложности физических процессов, происходящих в турбулентных течениях, важное значение имеют результаты экспериментальных работ, выполненных в 60—70-е годы Клайном, Кимом, Корино, Бродни и др. Посредством визуализации удалось установить реальную картину течения в пристеночной области. Ранее существовавшая схема пограничного слоя (ламинарный подслой, буферная область, область логарифмического профиля, внешняя область) существенно обогатилась дополнительной информацией о реальном течении. Согласно измерениям, ламинарный подслой оказался существенно тоньше (η < 0,336), чем предполагалось. В области до η = 50- 60 обнаружено нестационарное пространственное течение, обладающее достаточно регулярной структурой. Замечено также формирование замедленных струек жидкости у стенки, которые порождают вихревую пелену. Обнаружены стадии в развитии пристеночного течения: а) медленное всплывание замедленной жидкости, ее перемещение от стенки и затем вниз по потоку, при этом скорость перемещения возрастает; б) при достижении скорости определенной величины наступает неустойчивость, в результате возникают продольно ориентированные вихревые движения; в) при дальнейшем отходе вихревой пелены, от стенки наступает хаотическое движение, сопровождаемое выбросами жидкости на большие расстояния от стенки.
По мнению исследователей, при этом должны возникать большие касательные напряжения в области 4 < η < 32. Была установлена цикличность обновления течения у стенки (между выбросами), замечено засасывание нетурбулентной жидкости в пограничный слой.
Естественно, что эти процессы нуждаются в математическом моделировании. Ясно, что описанное выше формальное осреднение уравнений гидродинамики не может обеспечить понимание реальных процессов, так как при осреднении утеряются важные детали турбулентного течения.
Рассмотрим две модели турбулентности, устанавливающие конечные связи между характеристиками турбулентности.
Одновременный учет молекулярного и молярного (турбулентного) переносов во всей пристеночной области может быть произведен в соответствии с известной гипотезой Ван-Дрийста [142], в этом случае в пристеночной области длина пути перемешивания задается формулой

При этом трение определяется в виде

а μτ по формулам (2.5) и (2.9).
Гипотеза Ван-Дрийста нашла весьма широкое применение в расчетных работах. Заметим, что согласно этой гипотезе суммарная вязкость μ+ μτ зависит от трения τ трансцендентным образом (так как трение содержится также в выражении для η в показателе экспоненты в формуле (2.9), что не позволяет разрешить равенство (2.9)         относительно трения). Это создает определенные неудобства при численных расчетах.
Некоторые исследователи (например [118] и др.) с целью преодоления указанного недостатка вводят систему «поправок» к формуле (2.9). Смысл их состоит в том, что содержащаяся в (2.9) величина трения представляется рядом Тейлора в окрестности стенки (у = 0), при этом удерживаются лишь его первые члены. При отсутствии вдува и продольного градиента давления трение τ в формуле (2.9) иногда заменяется его значением на стенке xw . Вдув и градиент давления, если они существуют, учитываются
через первые члены ряда Тейлора. Естественно, при этом формула (2.9)    по существу заменяется приближенным выражением, что равноценно дополнительному предположению.
Конечные связи между характеристиками турбулентности устанавливает также модель коэффициентов полного переноса, предложенная в работе [75], согласно которой полная вязкость турбулентного потока вводится в виде суперпозиции молекулярной (ламинарной) и молярной (турбулентной) вязкостей. При этом следует учесть, что у стенки полная вязкость должна переходить в молекулярную, вдали от стенки — в турбулентную вязкость. Было принято
(2.10)
где коэффициенты к1 и к2 должны удовлетворять условиям
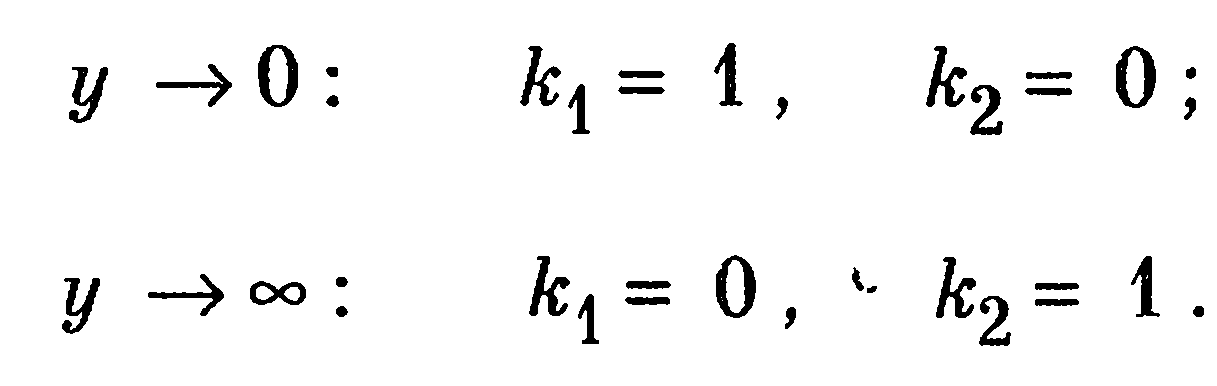(2.11)
При этом турбулентная вязкость μτ в формуле (2.10) определяется, в частности, по формуле Прандтля. Условия (2.11) удовлетворяются, если принять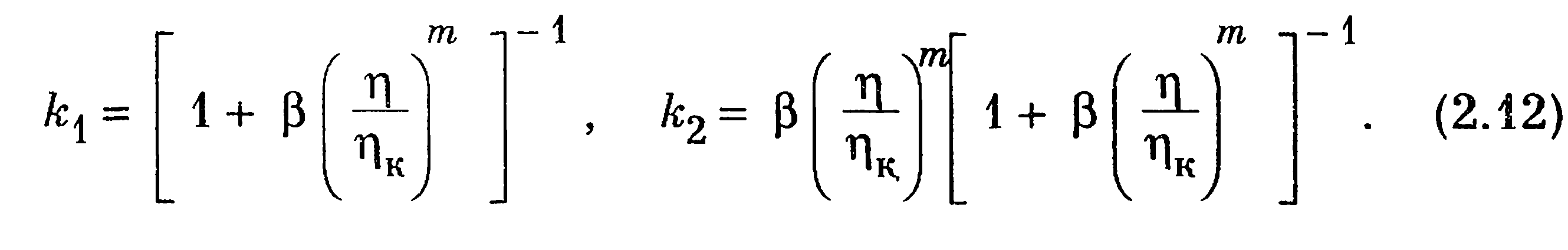
Здесь— критическое число Рейнольдса на границе ламинарного подслоя. Свободные параметры т и β следует рассматривать как константы турбулентности, которые могут быть определены из опытных данных. Важным является то, насколько эти константы турбулентности окажутся универсальными. Для нахождения констант т и β можно воспользоваться измерениями профилей скорости в пристеночной области у плоской непроницаемой пластины. Подставляя в уравнение
движения у стенки трение в видеи решая полученное уравнение, получаем следующее выражение профиля скорости в пристеночной области:

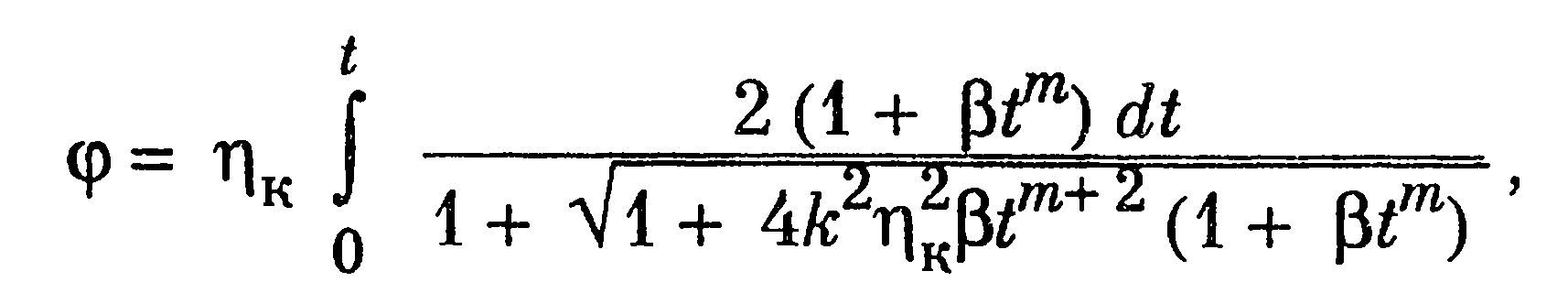
где

Наилучшее согласование с опытами расчетного профиля ско- рости получается при т~ 2 , β= к = 0,16 . При этом оказалось, что параметр β выражается через квадрат константы Кармана.
Заметим, что выбор величин к1-2 в виде (2.12) приводит к появлению неоправданного экстремума полной вязкости μΣ (незначительного по величине минимума) при малых значениях η. Этого можно избежать, если вместо (2.11), (2.12) во всей пристеночной области принять иное выражение для к1, а именно к1=1,     (2.13)
сохранив при этом выражение для к2 в виде (2.12). Как показывают вычисления, использование для к1 формулы (2.13) вместо (2.12) практически не оказывает влияния на результаты расчетов. Для того чтобы убедиться в универсальности введенных констант турбулентности т= 2, β= к , необходимо провести сопоставление расчетов с различными опытными данными в пристеночных областях. Представляет интерес порядок стремления к нулю величины добавочной вязкости μΣ- μ при у —> 0; нетрудно видеть, что при к1= 1.

Присутствующая в формуле (2.9) «новая константа» турбулентности А * оказывается представимой через известные «классические» константы турбулентности ηκ и к. Если перейти к пределу в выражении μΣ-μ при у—> 0 и при этом воспользоваться с одной стороны формулой (2.9), а с другой стороны выражениями (2.10), (2.12), и затем приравнять результаты предельного перехода, то оказывается, что А* = ηκ/к. Принимая ηκ= 10,4 и к = 0,4, получаем, что действительно значение А * = 26.
В качестве иллюстрации приведем результаты расчета поведения турбулентной вязкости, полученные с использованием модели коэффициентов полного переноса. На рис. 2.3, а показано распределение безразмерного коэффициента полной вязкости при течении в пристеночной области пластины (О — опыты Аббрехта), а на рис. 2.3, б в трубе радиусом г (О — опыты Никурадзе). Расчетные данные в обоих случаях подтверждаются опытными.

Были также проведены многочисленные расчеты разнообразных течений с использованием коэффициентов полного переноса, которые сопоставлялись с опытными данными. В качестве примеров использования модели коэффициентов полного переноса при расчете турбулентных пограничных слоев назовем следующие: расчеты пограничных слоев с резким изменением граничных условий [2]; задачи расчета пограничных слоев с ламинарными, переходными и турбулентными зонами течения и их приложение к определению теплоотдачи на турбинных профилях [79], [83]; расчеты пограничных слоев на проницаемых поверхностях [3], в частности на поверхностях турбинных лопаток при наличии распределенного вдува [81], [82] ; приложения модели к расчетам осесимметричных и пространственных пограничных слоев [86], [4], [110], [94]; расчеты двухкомпонентных пограничных слоев [85]; теоретическое предсказание точки отрыва на поверхности профиля [79] и расчет характеристик течения в зоне отрыва [60].

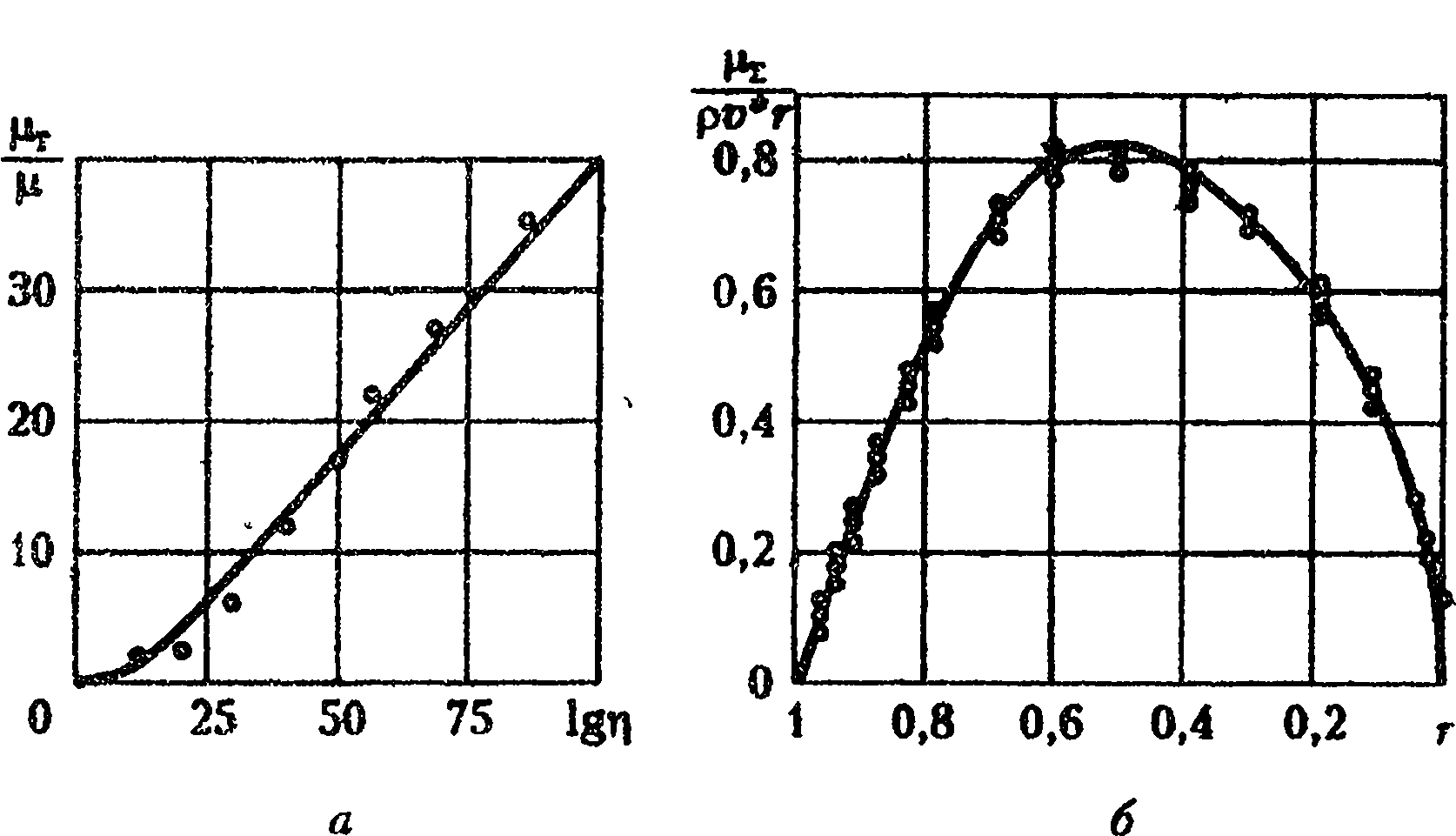
Рис. 2.3. Изменение безразмерной вязкости: а — расчет в пристеночной области пластины; б — расчет В. П. Бакалеева в трубе

Значительное развитие получило моделирование характеристик турбулентности, связанное с введением дополнительных дифференциальных уравнений, описывающих изменение тех или иных характеристик турбулентности. Структура этих уравнений «аналогична» обычно употребляемым уравнениям переноса. Они содержат конвективные, диффузионные, диссипативные, порождающие члены. Эти уравнения с самого начала являются приближенными (это следует из их вывода). Кроме того, такие уравнения так же, как и рассмотренные выше модели, содержат константы турбулентности, которые могут быть определены только из эксперимента. С возрастанием сложности модели количество констант турбулентности увеличивается, могут появиться вместо констант также функции, определяемые из опыта. Феноменологический подход с использованием дополнительных дифференциальных уравнений берет начало от работ А.Н. Колмогорова (1942 г.), Прандтля, Вигхардта (1945 г.). Однако широкий интерес к работам данного направления был проявлен несколько позже, что вероятно связано с развитием вычислительных возможностей.
Одной из первых работ, которая была доведена до численной реализации, по-видимому, является работа Г.С. Глушко [27], в которой содержится одно дополнительное дифференциальное уравнение (однопараметрическая модель) для кинетической энергии пульсационного движения, в дальнейшем эта модель была дополнена уравнением для масштаба. Дифференциальные уравнения для турбулентной вязкости были предложены в работах Ни, Коважного [136], А.Н. Секундова [71]. По мнению авторов этих работ, данные модели имеют преимущество при их применении к расчету неавтомодельных течений.
Уравнение непосредственно для турбулентного трения получено Брэдшоу с соавторами в [117]. Были выполнены расчеты для плоских течений, имеются обобщения и для пространственных [116], в последней работе предлагаются уравнения для отдельных компонент тензора напряжений Рейнольдса. Уравнение для интегрального масштаба турбулентности получено Ротта [137].
Широко распространены двухпараметрические модели [128], [138], [146]. Часто применяется модель Джонса—Лаундера [128], использующая уравнения энергии турбулентности е и скорости диссипации энергии турбулентности ε в виде

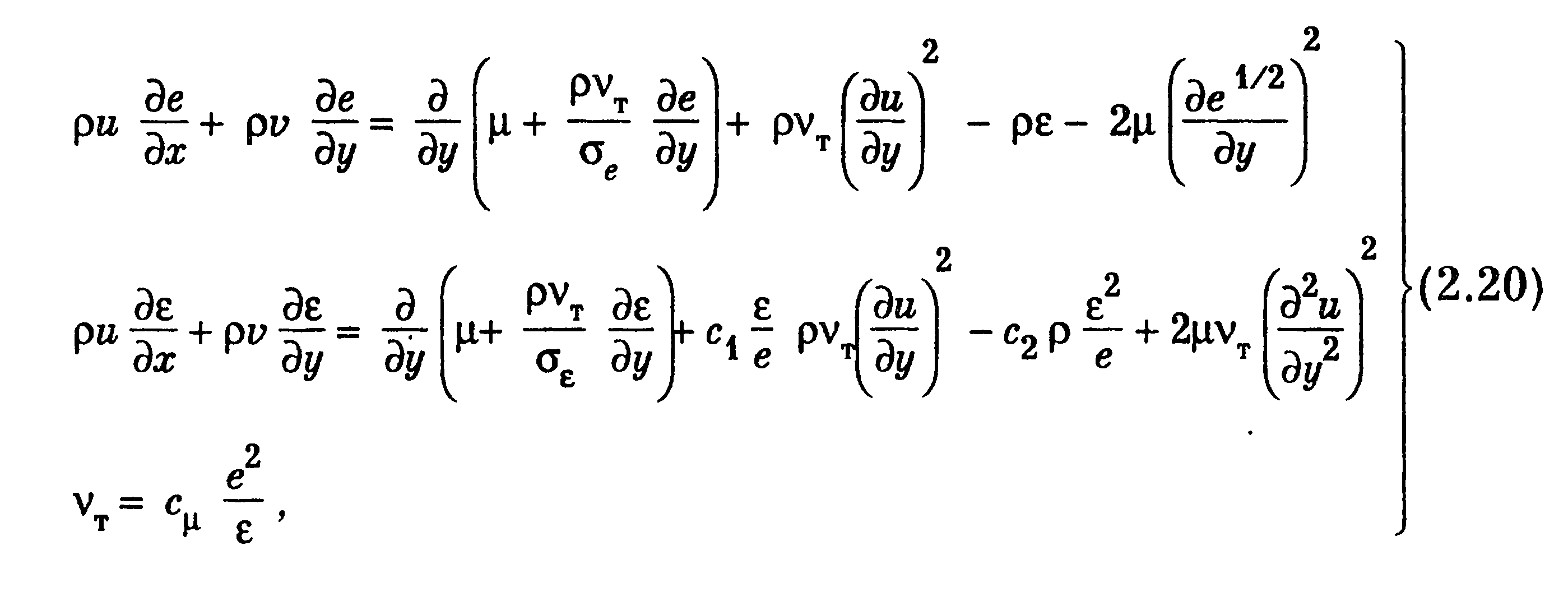
где принят набор констант: σе= 1, σΣ= 1,3, С|= 1,45, с2= 2, Сμ = 0,09.
В применении к различным течениям эта модель подвергалась модификациям. Так, для течений с низкими числами Рейнольдса было предложено

С использованием данной модели (часто называемой «к — ε») и различных ее модификаций (например, [54]) рассчитаны разнообразные течения и получено согласование расчетов с опытами.
Широкое применение имеет также модель, предложенная Саффменом [138] и развитая в многочисленных работах его последователей (например, [146]). В этой модели используются два дополнительных уравнения: для энергии турбулентности е и дополнительной завихренности со («псевдозавихренности») в виде

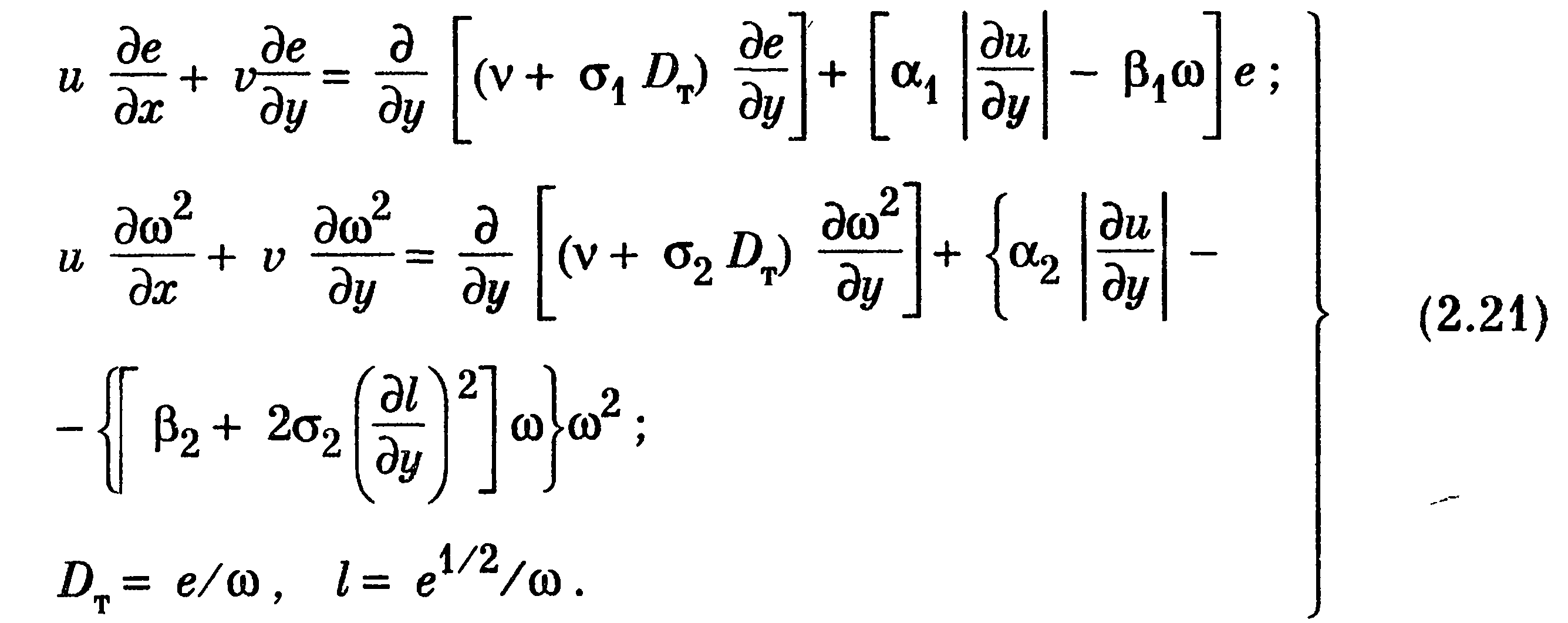
Здесь Dτ — коэффициент турбулентной диффузии, I — масштаб турбулентности.
Значения коэффициентов задаются в виде

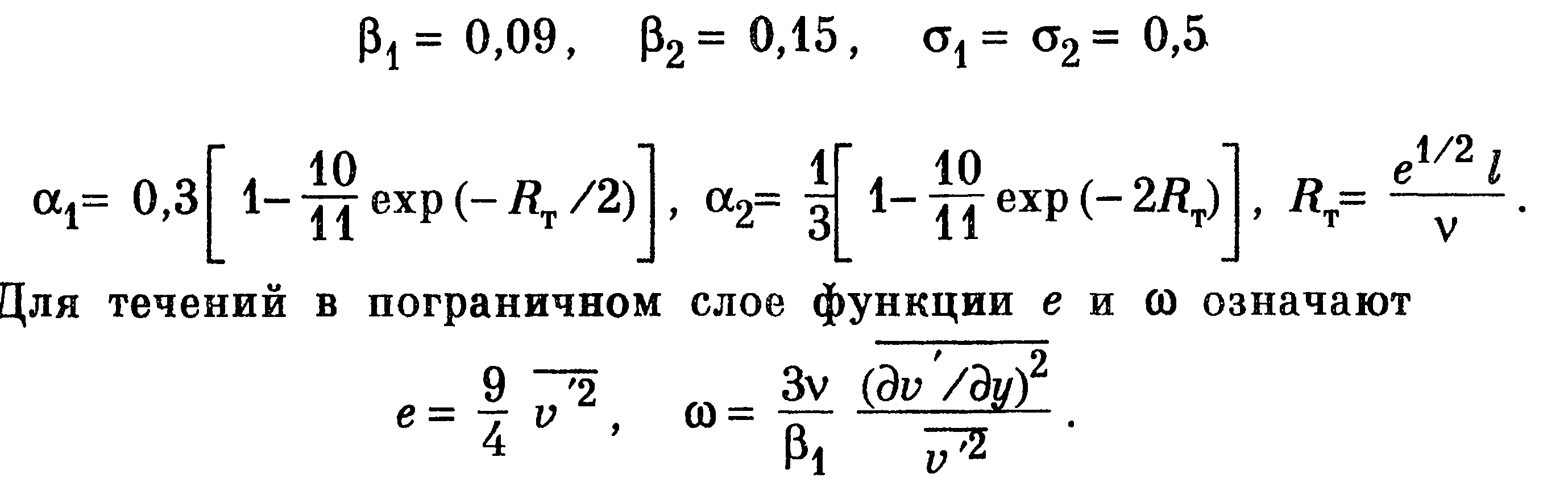
Следует заметить, что модель Саффмена весьма близка к модели, предложенной ранее в работе Колмогорова (1942 г.).
Существуют и более сложные многопараметрические модели. Оправданием введения более сложных моделей является предположение об их большей универсальности. Но в этих моделях содержится большее количество констант турбулентности, что сопряжено со значительными трудностями их выбора. В трехпараметрической модели Ханжалика—Лаундера [125] дополнительно к уравнениям переноса кинетической энергии турбулентности е и скорости диссипации кинетической энергии ε рассмотрено уравнение для касательного напряжения турбулентного трения ττ (таким образом, конечная связь между трением и кинетической энергией турбулентного движения отсутствует). В варианте трехпараметрической модели, предложенной В.Г. Лущиком, А.А. Павельевым, А.Е. Якубенко [40], используются уравнения энергии турбулентности е, турбулентного трения τт, а также уравнения для некоторой комбинации энергии турбулентности е и масштаба турбулентности L. На основе анализа выбираются два варианта этой комбинации. В первом F=е /L , что совпадает со скоростью диссипации энергии турбулентности, во втором варианте F= е/L , что совпадает с «псевдозавихренностью» по Саффмену. Рассматриваемая трехпараметрическая модель содержит свыше десяти констант турбулентности; был проведен ряд расчетов для относительно простых течений без изменения этих констант и при этом получено согласование с опытами.

Безусловный интерес представляет применение многопараметрических моделей к расчету более сложных задач, к которым относится расчет внешнего теплообмена на турбинных профилях. Заметим, что усложнение моделей турбулентности не должно быть чрезмерным, так как при этом физическая интерпретация отдельных членов в дополнительных уравнениях затрудняется. Во многих случаях для практических целей достаточно применения двухпараметрических к однопараметрических моделей, а для течений в пограничных слоях часто достаточно использования конечных моделей. Следует заметить, что существующие в настоящее время разнообразные модели турбулентности имеют ограниченную универсальность и обеспечивают достаточно низкую точность (точность в пределах 20% считается хорошей). Одна из трудностей применения моделей турбулентности связана с расчетом пограничных слоев при относительно малых числах Рейнольдса, в частности в достаточно малой окрестности стенки, где вид течения имеет промежуточный характер между ламинарным и турбулентным. Анализ восьми различных модификаций моделей турбулентности при малых числах Рейнольдса представлен в обзоре [54]. При этом использовались тестовые задачи с известными из эксперимента данными. Сделан вывод, что лишь некоторые модели оказались достаточно эффективными (модификации модели [128], а также модели [138]). Однако, по мнению авторов обзора [54], и эти лучшие модели нуждаются в усовершенствовании для использования их в расчетах при малых числах Рейнольдса.

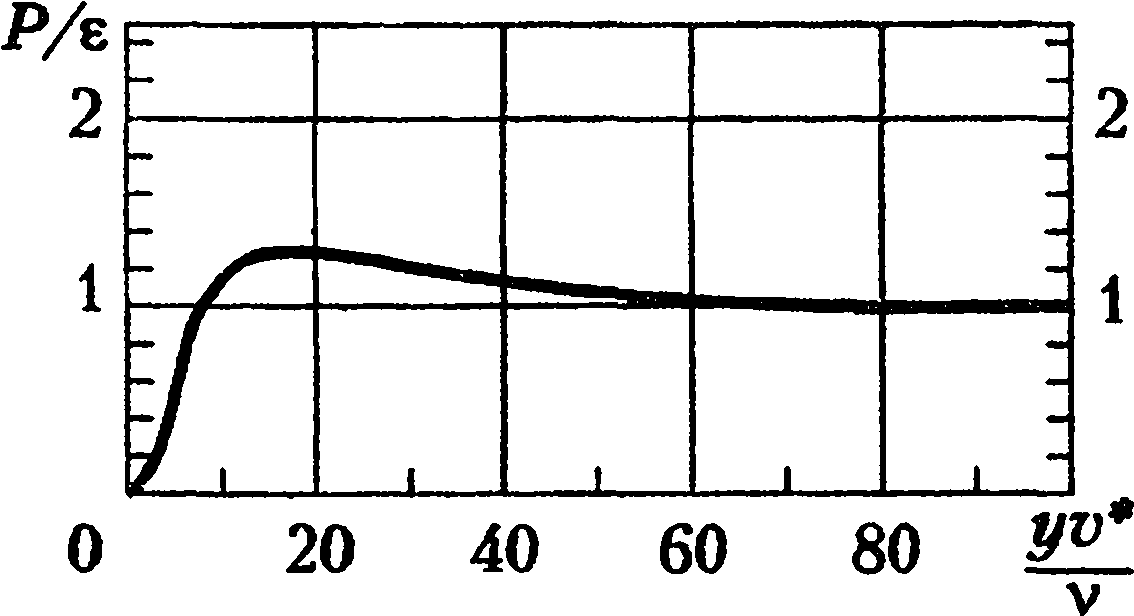
Рис. 2.4. Отношение скорости генерации к скорости диссипации энергии турбулентности в пристеночной области
По-видимому, затруднения, связанные с применением много- параметрических моделей турбулентности при достаточно малых числах Рейнольдса вызваны тем, что эти модели разрабатывались для развитых турбулентных течений, чем и определялся выбор констант (например, в моделях группы «к-ε» пять констант и дополнительные поправочные функции). Наблюдаемое при низких числах Рейнольдса расхождение расчетов с опытами требует, в частности, иного подбора констант. Для преодоления указанных затруднений можно использовать в области малых чисел Рейнольдса конечные модели турбулентности, которые разрабатывались специально для пристеночной области. Расчеты с использованием этих моделей вполне удовлетворительно согласуются с опытами в пристеночной области, включая логарифмическую область, да и на внешней стороне пограничного слоя отличия от опыта невелики. Указанное согласование в основной части пограничного слоя можно объяснить тем, что конечные модели опираются на гипотезу Прандтля, которая справедлива в случае равновесного пограничного слоя, когда порождение турбулентности уравновешивается ее диссипацией. Согласно данным, приведенным в обзоре [54], действительно в значительной части пристеночной области пограничного слоя скорость генерации турбулентной энергии и скорость ее диссипации приблизительно равны; различие между ними увеличивается непосредственно у стенки (рис. 2.4).
Но как раз в этой области указанные выше конечные модели дают отличающиеся от гипотезы Прандтля результаты (в этих моделях имеются демпфирующие множители, действующие в непосредственной близости от стенок).
Для расчета пограничных слоев при малых числах Рейнольдса целесообразно использовать конечные модели (например, формулы (2.17)       — (2.19)). Это можно сделать и в сочетании с использованием моделей более высокого уровня (например, двухпараметрической модели Саффмена). С этой целью необходимо обобщить локальное число Рейнольдса rt (rt = μτ/μ), определив его не с использованием
формулы Прандтля, как это было сделано выше, а через характеристики турбулентности, для определения которых обычно вводятся дополнительные дифференциальные уравнения. Так, можно принять
(2.22)
и воспользоваться формулами (2.17) или (2.18).
Для нахождения распределения величин е и ω можно использовать, например, уравнения (2.21). Такой подход позволит получить лучшее согласование расчетов с опытами во всем пограничном слое. Кроме того, он дает возможность естественным образом учесть влияние внешней турбулентности.