Явления в асинхронной машине при неподвижном роторе
Физическая сущность явлений в асинхронной машине и трансформаторе имеет много общего, поэтому целесообразно начать изучение асинхронных машин с трансформаторного режима при неподвижном роторе (![]() ).
).
Рассмотрим явления в трехфазной асинхронной машине, полагая, что все величины являются синусоидальными функциями времени, а магнитное поле в воздушном зазоре распределено по гармоническому закону. Высшими пространственными гармониками поля пренебрегаем. Обмотку ротора будем считать фазной. Пусть вначале обмотка ротора разомкнута, а обмотка статора включена в сеть на напряжение ![]() (рис. 4.3, а).
(рис. 4.3, а).
Симметричная система токов ![]() , протекающих по фазам обмотки статора под действием приложенного напряжения
, протекающих по фазам обмотки статора под действием приложенного напряжения ![]() , создает основную гармонику МДС с амплитудой
, создает основную гармонику МДС с амплитудой
![]() .
.
Под действием этой МДС в машине образуется магнитный поток, который обычно разделяют на основной поток Ф, сцепленный с обмотками статора и ротора, и поток рассеяния ![]() , сцепленный только с обмоткой статора,
, сцепленный только с обмоткой статора,
![]() .
.
Основной магнитный поток наводит в обмотках статора и ротора ЭДС
![]() ;
;
![]() .
.
Для удобства дальнейшего анализа обмотку ротора приведем к обмотке статора. Приведенные величины, как и в трансформаторе, будем обозначать символами со штрихами. Коэффициент приведения по напряжению определяется как отношение ЭДС ![]() и
и ![]() :
:
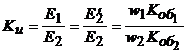 .
.
Появление в формуле для ![]() отношения обмоточных коэффициентов обусловлено характером образования магнитного поля в асинхронной машине. В отличие от трансформатора первая гармоника магнитного поля асинхронной машины зависит от конструкции обмотки.
отношения обмоточных коэффициентов обусловлено характером образования магнитного поля в асинхронной машине. В отличие от трансформатора первая гармоника магнитного поля асинхронной машины зависит от конструкции обмотки.

ЭДС ![]() и
и ![]() можно также выразить через ток
можно также выразить через ток ![]() , используя комплексную форму записи величин
, используя комплексную форму записи величин
![]() ,
,
где ![]() - сопротивление намагничивающего контура;
- сопротивление намагничивающего контура; ![]() ,
, ![]() - активная и реактивная составляющие сопротивления намагничивающего контура.
- активная и реактивная составляющие сопротивления намагничивающего контура.
В обмотке статора кроме ЭДС ![]() существует еще ЭДС
существует еще ЭДС ![]() от потока рассеяния
от потока рассеяния ![]() . Действующее значение этой ЭДС представляется комплексом
. Действующее значение этой ЭДС представляется комплексом
![]() ,
,
где ![]() - индуктивное сопротивление рассеяния обмотки статора.
- индуктивное сопротивление рассеяния обмотки статора.
Напряжения, ЭДС и токи фаз обмоток статора и ротора должны удовлетворять уравнениям, которые в комплексной форме записываются аналогично уравнениям трансформатора

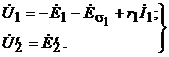 (4.1)
(4.1)
Выражая ЭДС ![]() ,
, ![]() и
и ![]() через ток
через ток ![]() , получим
, получим
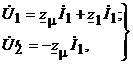 (4.2)
(4.2)
где ![]() .
.
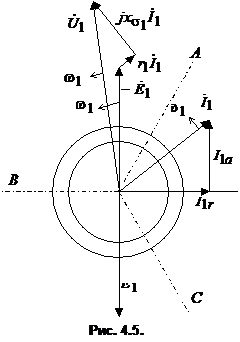
Этим уравнениям соответствует схема замещения асинхронной машины с неподвижной и разомкнутой обмоткой ротора (рис. 4.4). Данная схема аналогична схеме замещения трансформатора на холостом ходу. Отличие состоит лишь в соотношении параметров. Наличие воздушного зазора в машине приводит к существенному снижению реактивной составляющей сопротивления намагничивающего контура ![]() и, следовательно, к увеличению тока намагничивания. В асинхронных машинах ток намагничивания составляет 20-50% от номинального тока, а в трансформаторе он на порядок меньше. По уравнениям (4.1) можно построить также векторную диаграмму, задав напряжение вектора ЭДС
и, следовательно, к увеличению тока намагничивания. В асинхронных машинах ток намагничивания составляет 20-50% от номинального тока, а в трансформаторе он на порядок меньше. По уравнениям (4.1) можно построить также векторную диаграмму, задав напряжение вектора ЭДС ![]() (рис. 4.5). Если совместить эту диаграмму с пространственной диаграммой, то можно получить мгновенные значения фазных напряжений ЭДС и токов, проецируя вращающиеся с угловой скоростью
(рис. 4.5). Если совместить эту диаграмму с пространственной диаграммой, то можно получить мгновенные значения фазных напряжений ЭДС и токов, проецируя вращающиеся с угловой скоростью ![]() векторы
векторы ![]() ,
, ![]() и
и ![]() на неподвижные оси АВС.
на неподвижные оси АВС.
Рассмотрим теперь процессы в асинхронной машине с неподвижным ротором и короткозамкнутой обмоткой ротора (рис. 4.6, а).
При включении обмотки статора на напряжение ![]() фазные токи
фазные токи ![]() создают основную гармонику МДС
создают основную гармонику МДС ![]() с амплитудой
с амплитудой
![]() .
.
Токи ротора ![]() , направленные, в соответствии с правилом Ленца, навстречу токам
, направленные, в соответствии с правилом Ленца, навстречу токам ![]() , создадут основную гармонику МДС
, создадут основную гармонику МДС ![]() с амплитудой
с амплитудой
![]() .
.

Число фаз обмотки ротора ![]() в общем случае не равно числу фаз обмотки статора
в общем случае не равно числу фаз обмотки статора ![]() . МДС
. МДС ![]() и
и ![]() образуют результирующую МДС
образуют результирующую МДС ![]() , которая создает основной магнитный поток
, которая создает основной магнитный поток ![]() , сцепленный с обеими обмотками.
, сцепленный с обеими обмотками.
Связь между этими МДС в комплексной форме определяется уравнением
![]() .
.
Выражая МДС через соответствующие токи, получим
 ,
,
где ![]() - ток намагничивания, протекающий по обмотке статора.
- ток намагничивания, протекающий по обмотке статора.
Отсюда находим выражение для тока намагничивания ![]() :
:

или
![]() , (4.3)
, (4.3)
где 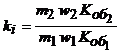 - коэффициент приведения обмотки ротора к обмотке статора по току.
- коэффициент приведения обмотки ротора к обмотке статора по току.
Полученное уравнение называется уравнением токов.
Ток намагничивания ![]() по определению создает в машине основной магнитный поток Ф, который, сцепляясь с обмотками статора и ротора, наводит в них ЭДС
по определению создает в машине основной магнитный поток Ф, который, сцепляясь с обмотками статора и ротора, наводит в них ЭДС

Кроме основного потока в машине существуют также потоки рассеяния ![]() и
и ![]() (рис. 4.6, б). Каждый из этих потоков сцепляется только со своей обмоткой и наводит в ней ЭДС рассеяния
(рис. 4.6, б). Каждый из этих потоков сцепляется только со своей обмоткой и наводит в ней ЭДС рассеяния ![]() и
и ![]() соответственно.
соответственно.
Действующие значения этих ЭДС можно выразить через соответствующие токи в комплексной форме:
![]()
С целью упрощения дальнейшего анализа выполним приведение обмотки ротора к обмотке статора, используя соотношения
![]() и
и ![]() .
.
После приведения получаем
![]() ;
; ![]() ,
,
где ![]() - приведенное значение индуктивного сопротивления рассеяния обмотки ротора;
- приведенное значение индуктивного сопротивления рассеяния обмотки ротора; ![]() - коэффициент приведения обмотки ротора к обмотке статора по сопротивлению.
- коэффициент приведения обмотки ротора к обмотке статора по сопротивлению.
В соответствии со вторым законом Кирхгофа напряжения, ЭДС и токи обмотки статора и ротора должны удовлетворять уравнениям
 (4.4)
(4.4)
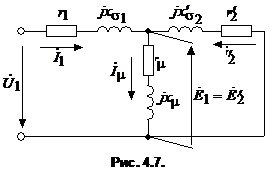
где ![]() - приведенное значение активного сопротивления обмотки ротора.
- приведенное значение активного сопротивления обмотки ротора.
Уравнения напряжений (4.4) совместно с уравнением тока (4.3) образуют полную систему уравнений асинхронной машины для анализа установившихся режимов.
Уравнения показывают, что асинхронную машину можно заменить Т-образной схемой замещения (рис. 4.7), аналогичной схеме замещения трансформатора в режиме короткого замыкания.
Таким образом, при неподвижном роторе асинхронная машина работает как трансформатор, в котором электрическая энергия статора за вычетом потерь переходит в ротор, где, не совершая никакой полезной работы, превращается в тепло.

