Механической характеристикой называется зависимость 
при 
и 
. При выводе уравнения механической характеристики будем исходить из базовых соотношений для электромагнитного момента:
. (4.8)
Расчет тока ротора 
выполним по схеме замещения асинхронной машины (рис. 4.8) методом эквивалентного генератора.
Разомкнем цепь ротора и найдем напряжение эквивалентного генератора:
,
где 
.
Для получения сопротивления эквивалентного генератора закоротим источник напряжения 
,
.
Полученные соотношения позволяют определить ток ротора:
.
Отсюда, полагая 
, получаем действующее значение тока ротора:
.
С учетом этого выражения формула для электромагнитного момента (4.8) приобретает вид
. (4.9)
Выражение (4.9) удобно для анализа механической характеристики 
, так как при 
и 
оно содержит только одну переменную s.
Исследуем сначала общий характер зависимости 
:
при 
;
при 
;
при 
;
при 
.
Этим условиям удовлетворяет кривая 
, представленная на рис. 4.11.
Кривая имеет экстремумы при скольжении 
, которое называется критическим скольжением. Это скольжение определяется из условия 
.
Для удобства дифференцирования введем обозначения: 
; 
; 
; 
. Тогда выражение для электромагнитного момента преобразуется к виду
.
Дифференцируя это выражение по y, получим
.
Отсюда после преобразований имеем
.
Переходя вновь к скольжению, получим
. (4.10)
Подставляя значение 
в (4.9), определяем максимальный момент асинхронной машины:
, (4.11)
знак «+» относится к двигательному режиму, а «-» - к генераторному режиму.
Для асинхронных машин большой мощности можно считать, что 
и 
, тогда
; (4.12)
. (4.13)
Отсюда следует, что максимальный момент асинхронной машины прямо пропорционален квадрату напряжения сети 
и обратно пропорционален 
.
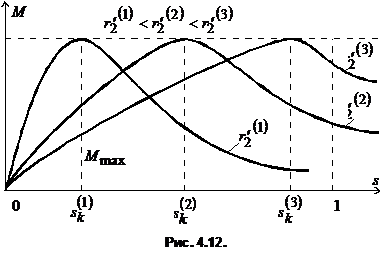
Положение максимума зависит от сопротивления ротора 
. На рис. 4.12 показана механическая характеристика асинхронной машины в режиме двигателя. Чем больше 
, тем больше 
, при этом, как следует из (4.13), величина 
остается неизменной.
Кратность максимального момента 
. Более высокие значения 
имеют быстроходные двигатели с малым числом полюсов.
Выражение (4.9) позволяет определить пусковой момент двигателя, если подставить в него 
:
. (4.14)
Пусковой момент 
так же, как и максимальный 
, пропорционален квадрату напряжения, но его величина в отличие от 
зависит от сопротивления 
. Как следует из (4.10), пусковой момент будет равен максимальному, если
. (4.15)
При упрощенных расчетах механическую характеристику определяют с помощью формулы Клосса:
. (4.16)
Для этого необходимо знать две точки на реальной механической характеристике. Их можно получить по каталожным данным для пускового и номинального режимов. В этом случае погрешность формулы Клосса составляет 10-15%.
