Электрические машины - Уравнения напряжений и векторные диаграммы

Уравнения напряжений и векторные диаграммы синхронного генератора без учета насыщения

Неявнополюсный генератор

В ненасыщенной машине магнитная цепь является линейной, поэтому при расчете результирующего магнитного поля можно применять метод наложения. МДС обмотки возбуждения создает магнитный поток , который, сцепляясь с обмоткой статора, наводит в ней ЭДС . МДС обмотки статора создает поток реакции якоря и поток рассеяния . Каждый из этих потоков сцеплен с обмоткой статора и наводит в ней ЭДС и соответственно. Сумма ЭДС, действующих в обмотке статора, определяет напряжение генератора за вычетом падения напряжения на активном сопротивлении,
. (5.6)
Действующее значение ЭДС холостого хода можно определить по спрямленной характеристике холостого хода (рис. 5.6), а ЭДС реакции якоря можно выразить через ток якоря :
,
где - индуктивное сопротивление реакции якоря.
Аналогичные выражения можно получить для ЭДС рассеяния :
,
где - индуктивное сопротивление рассеяния обмотки статора.
С учетом полученных выражений для ЭДС и уравнение (5.6) преобразуется к виду
, (5.7)

где - полное индуктивное сопротивление якоря; - внутреннее сопротивление генератора.
Согласно уравнению (5.7) синхронный генератор можно представить источником ЭДС с внутренним сопротивлением (рис. 5.11). Геометрической интерпретацией этого уравнения являются векторные диаграммы, приведенные на рис. 5.12.
Как следует из схемы замещения и векторных диаграмм, в нерегулируемом генераторе (,) напряжение зависит от величины и характера нагрузки. Если нагрузка активно-индуктивная, то напряжение снижается с увеличением нагрузки вследствие размагничивающего действия поля реакции якоря (рис. 5.12, а). Если нагрузка активно-емкостная, то напряжение генератора возрастает, так как реакция якоря носит намагничивающий характер (рис. 5.12, б). Чтобы поддержать напряжение генератора при изменении нагрузки постоянным, регулируют ток возбуждения , увеличивая его при активно-индуктивной нагрузке и уменьшая при активно-емкостной нагрузке.
Угол Q между векторами и называют углом нагрузки. В генераторном режиме вектор всегда опережает вектор , и угол Q считается положительным.
При расчетах различных режимов генератора уравнение (5.7) записывают в относительных единицах, принимая в качестве базисного напряжения номинальное фазное напряжения , а в качестве базисного тока - номинальный фазный ток . Величина базисного сопротивления определяется отношением
.
Для современных генераторов с неявновыраженными полюсами (турбогенераторы) параметры в относительных единицах имеют следующие значения:

;
;
.

Явнополюсный генератор

При составлении уравнения напряжений ненасыщенного явнополюсного генератора можно также использовать метод наложения. Здесь МДС обмотки возбуждения , как и в случае неявнополюсного генератора, создает поток , который, сцепляясь с обмоткой статора, наводит в ней ЭДС . Магнитный поток обмотки статора представим в виде суммы трех составляющих -, и . Каждый из этих потоков, сцепляясь с обмоткой статора, наводит в ней ЭДС , и соответственно. Напряжение генератора в этом случае будет равно геометрической сумме этих ЭДС минус падение напряжения на активном сопротивлении:
. (5.8)
Модуль ЭДС определяется по спрямленной характеристике холостого хода (рис.5.6) при заданном значении тока возбуждения . Для определения ЭДС реакции якоря и разложим ток статора на продольную и поперечную составляющие:
,
где ; .
Току соответствует МДС , определяющая поток продольной реакции якоря, а току соответствует МДС , определяющая поток поперечной реакции якоря. Поэтому выражения для ЭДС и можно представить в виде
;
,
где - индуктивное сопротивление реакции якоря по продольной оси; - индуктивное сопротивление реакции якоря по поперечной оси.
ЭДС рассеяния определяется полным током статора
.
Выразив ЭДС , и через соответствующие индуктивные сопротивления и токи, преобразуем уравнение (5.8) к виду
.
Принимая во внимание, что , получим
,
или
, (5.9)
где - полное индуктивное сопротивление якоря по продольной оси; - полное индуктивное сопротивление якоря по поперечной оси.
Уравнению (5.9) соответствуют векторные диаграммы для активно-индуктивной (рис. 5.13, а) и активно-емкостной (рис. 5.13, б) нагрузки.
Так же, как и в неявнополюсном генераторе, напряжение явнополюсного генератора снижается с увеличением активно-индуктивной нагрузки и растет при увеличении активно-емкостной нагрузки. Формально уравнение (5.9) можно свести к уравнению неявнополюсной машины, заменив в нем ток на :
,

или
, (5.10)

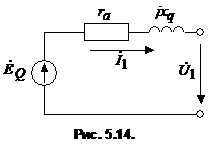
где - эквивалентная ЭДС явнополюсного генератора. Замена ЭДС на позволяет воспользоваться простой схемой замещения явнополюсного синхронного генератора (рис. 5.14) при аналитических расчетах его режимов работы.
Внутреннее сопротивление явнополюсного генератора в этом случае определяется величиной
.

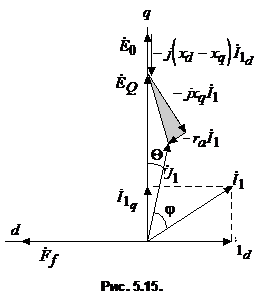
На рис. 5.15 приведена векторная диаграмма, построенная по уравнению (5.10) для активно-индуктивной нагрузки. При упрощенных расчетах ЭДС принимают постоянной, пренебрегая ее изменением при изменении тока .
Параметры современных синхронных генераторов явнополюсного исполнения в относительных единицах имеют следующие значения:

;
;
;
.