При работе синхронной машины параллельно с сетью ротор независимо от нагрузки вращается с постоянной частотой, но положение ротора относительно поля статора зависит от величины нагрузки. Это положение характеризуется углом q между вектором ЭДС 
и отрицательным направлением вектора напряжения сети 
(рис. 5.33). Любое изменение факторов, влияющих на нагрузку (напряжения сети 
, тока возбуждения 
или внешнего момента 
) приводит к изменению положения ротора. Новое значение угла q устанавливается после переходного процесса, имеющего колебательный характер. Поскольку вектор напряжения сети 
вращается с постоянной угловой скоростью 
, соответствующей частоте сети 
, то колебания угла q происходят в результате механических качаний ротора относительно синхронной скорости.
Рассмотрим характер качаний ротора, вызванных малым изменением внешнего момента
.
Движение ротора описывается дифференциальными уравнениями
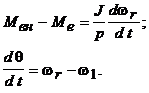
При качаниях ротора электромагнитный момент 
представляет собой сумму синхронного 
и асинхронного 
моментов,
.
Синхронный момент 
является нелинейной функцией угла q (рис. 5.39), а асинхронный момент 
является нелинейной функцией скольжения 
(рис. 4.11). Используя линеаризацию этих нелинейных функций с помощью соотношений
;
и учитывая, что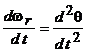 
, преобразуем уравнения движения ротора к виду
.
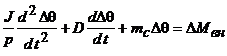Решение этого уравнения известно:
,
где 
, 
- постоянные интегрирования; 
, 
- корни характеристического уравнения
,
.
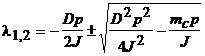Подкоренное выражение определяет собственную частоту колебаний ротора:
,
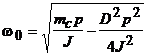а первое слагаемое характеризует коэффициент затухания качаний 
. При корнях 
решение дифференциального уравнения движения ротора можно записать в виде
,
где 
.
На рис. 5.68 показан характер движения ротора при малом изменении внешнего момента. Период собственных колебаний ротора составляет 
, а время затухания 
.
При уменьшении коэффициента демпфирования D частота собственных колебаний ротора возрастает и возрастает время переходного процесса 
. При больших коэффициентах демпфирования D (жесткая механическая характеристика) или малых коэффициентах синхронизирующего момента 
(работа вблизи предела статической устойчивости), когда
,
корни характеристического уравнения 
и 
получаются действительными, поэтому переходный процесс имеет апериодический характер.
В условиях эксплуатации синхронных машин наряду с малыми возмущениями происходят и большие возмущения (внезапные короткие замыкания, отключение линии, включение значительной нагрузки и т. п.), при которых изменение угла q может достигать опасных значений по условию устойчивости параллельной работы синхронной машины с сетью. Способность синхронной машины оставаться в синхронизме при больших возмущениях называется динамической устойчивостью.
Наиболее простым методом исследования динамической устойчивости является метод площадей. В основе метода лежит угловая характеристика синхронной машины в переходном режиме 
. Так как качания ротора происходят сравнительно медленно, то сверхпереходными и апериодическими токами статора пренебрегают, а расчет периодических токов статора по осям d и q выполняют с помощью схем замещения (рис. 5.69).
Согласно схеме рис.5.69, а сопротивление синхронной машины по оси d в переходном режиме меняется с 
на 
, поэтому уравнение напряжений преобразуется к виду
,
где 
.
Соответствующим образом изменяется и уравнение угловой характеристики
.
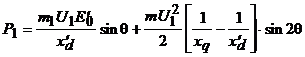Так как 
, то в отличие от статической характеристики 
максимум этой кривой смещается в сторону углов 
.
Рассмотрим переходный процесс в синхронном генераторе при снижении напряжения сети 
, вызванном удаленным коротким замыканием. Пусть до аварии генератор работал с некоторой нагрузкой 
. Угол нагрузки 
определяется по угловой характеристике статического режима (рис. 5.70, кривая 1). В результате аварии напряжение сети снижается и угловая характеристика приобретает вид, представленный на рис. 5.70, кривая 2.
Аналогичным образом изменяется и электромагнитный момент генератора
.
В исходном режиме электромагнитный момент 
был равен внешнему,
.
В первый момент аварийного режима электромагнитный момент снижается до величины, соответствующей точке «а» на кривой 2 (рис. 5.70). Поэтому возникнет положительный динамический момент
,
под действием которого ротор ускоряется (рис. 5.71). Процесс ускорения ротора будет происходить до тех пор, пока угол q не достигнет величины 
. Во время ускорения кинетическая энергия ротора возрастет на величину
.
На рис. 5.70 энергия ускорения 
равна площади треугольника «abc»,
,
где 
- площадка ускорения.
В точке «с» внешний и электромагнитный моменты равны, но не равны угловые скорости вращения ротора 
и поля 
, поэтому в силу инерции ротора угол q будет продолжать увеличиваться. При этом электромагнитный момент 
превысит внешний 
, и в сеть будет поступать больше мощности, чем развивает турбина,
,
поэтому ротор начнет тормозиться.
Этот процесс будет продолжаться до тех пор, пока не израсходуется запасенная кинетическая энергия 
. Угловая скорость ротора вновь станет синхронной, а угол q достигнет максимального значения 
. Величина 
определяется из условия
,
где 
- площадь торможения.
Если максимально возможная площадь торможения 
будет меньше 
, то угол q превысит критическое значение 
. Электромагнитный момент 
станет ниже 
. Ротор, не достигнув синхронной скорости, вновь начнет ускоряться, и генератор выпадет из синхронизма. Таким образом, условие
является критерием динамической устойчивости. Отношение 
характеризует запас динамической устойчивости: чем меньше площадка ускорения 
и больше площадка торможения 
, тем выше запас динамической устойчивости.
На динамическую устойчивость синхронной машины большое влияние оказывает регулирование возбуждения (рис. 5.72). При увеличении тока возбуждения площадка ускорения уменьшается на величину 
, а площадка торможения возрастает на величину 
. При больших возмущениях регулирование возбуждения выполняется в форме форсировки (подачи на обмотку возбуждения максимального напряжения возбуждения
,
где 
- кратность форсировки). Эффективность форсировки тем выше, чем больше кратность форсировки 
и чем выше быстродействие возбудителя. Кратность форсировки современных возбудителей составляет 2¸2,5, а быстродействие зависит от типа возбудителя.
Наибольшее быстродействие имеют тиристорные возбудители, питающиеся от независимого источника. Наиболее инерционными являются возбудители, выполненные на основе машины постоянного тока (электромашинные возбудители).
