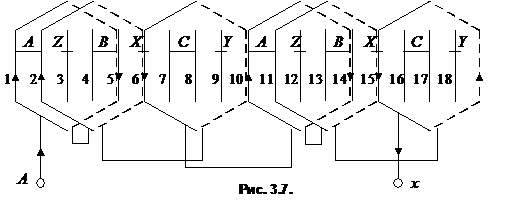
Магнитное поле в электрической машине создается токами, протекающими по ее обмоткам (рис. 3.8). Расчет магнитного поля производится на основе закона полного тока
(3.1)
для любой силовой линии поля. Правая часть уравнения (3.1) представляет собой сумму магнитодвижущих сил (МДС) всех фаз обмотки, а левая часть - падение магнитного потенциала на всех участках магнитной цепи вдоль силовой линии.
Для решения уравнения (3.1) примем допущения, что магнитопровод не насыщен, магнитная проницаемость стали 
, воздушный зазор равномерный и гладкий, величина d мала по сравнению с диаметром 
, проводники обмотки статора расположены на его внутренней поверхности и имеют бесконечно малые размеры.
При 
напряженность магнитного поля внутри магнитопровода 
, и падения магнитного потенциала на стальном участке магнитной цепи не происходит. Поэтому циркуляцию вектора Н можно представить в виде определенного интеграла
,
численно равного падению магнитного потенциала на двух воздушных зазорах.
При малом d поле в воздушном зазоре равномерно, поэтому напряженность поля вдоль силовых линий 
. Следовательно, падение магнитного потенциала в воздушном зазоре можно представить в виде
.
Отсюда находим напряженность магнитного поля
и соответствующую ей магнитную индукцию в зазоре
. (3.2)
Выражение (3.2) позволяет определить пространственное распределение магнитной индукции вдоль расточки статора, если известен характер распределения МДС трехфазной обмотки.
Магнитодвижущая сила секции
Секция является простейшим элементом трехфазной обмотки. Поэтому для определения результирующей МДС трехфазной обмотки рассмотрим сначала МДС секции. Пусть на статоре уложено по одной секции на каждом полюсном делении. Шаг секции 
. По секциям протекает ток 
, равный току параллельной ветви фазы:
.
Вид возникающего при этом магнитного поля на одном полюсном делении показан на рис. 3.9. Любая силовая линия магнитного поля сцеплена с полным током секции 
, поэтому поле, созданное секцией, будет постоянным на протяжении всего полюсного деления,
.
Будем считать магнитную индукцию положительной, если силовые линии идут вверх (южный полюс), и отрицательной, если силовые линии идут вниз (северный полюс). В соответствии с этим условием при принятом направлении тока поле внутри секции будет положительным, образующим южный полюс, а за пределами секции - отрицательным, образующим северный полюс.
МДС секции, приходящуюся на один полюс, обозначим через 
. При равномерном воздушном зазоре МДС каждого полюса равны, поэтому
. (3.3)
МДС секции изменяется скачком при пересечении активной стороны секции, увеличиваясь, если ток направлен к нам, и уменьшаясь, если ток направлен от нас. Величина скачка МДС равна полному току секции 
(рис. 3.9, пунктирная линия).
Таким образом, МДС секции представляет собой неподвижную в пространстве прямоугольную волну, пульсирующую, согласно (3.3), во времени с частотой питающей сети.
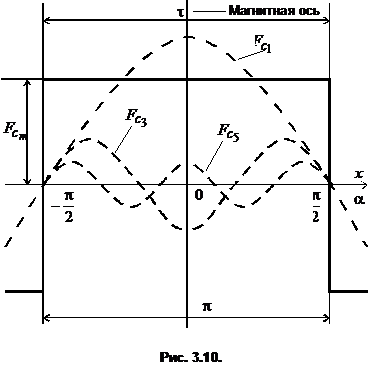
Для дальнейшего анализа поля удобно пространственную кривую МДС разложить в ряд Фурье. Выполним разложение кривой МДС (рис. 3.10) в пределах полюсного деления для момента времени 
, когда МДС секции принимает максимальное значение
.
Начало отсчета совместим с магнитной осью секции. Исходная функция является четной и симметричной относительно оси абсцисс, поэтому в разложении будут содержаться только нечетные гармоники с косинусными членами:
,
где 
- пространственный угол; n - порядок гармоники.
Амплитуды гармонических составляющих определяются по формуле
.
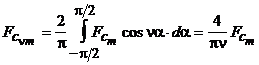Первая гармоника называется основной, а остальные - высшими пространственными гармониками. Амплитуда высшей гармоники обратно пропорциональна ее порядку. Среди высших гармоник наиболее значительными являются 3-я, 5-я, 7-я гармоники.
Эффективным способом подавления высших гармоник является укорочение шага секции. На рис. 3.11 представлена МДС секции с укороченным шагом 
, где 
- относительный шаг секции.
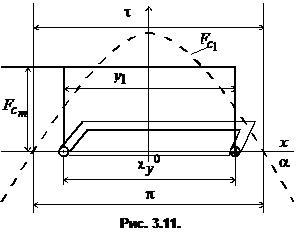
В угловом измерении шаг определяется величиной
.
Раскладывая кривую (рис. 3.11) в ряд Фурье, получим
,
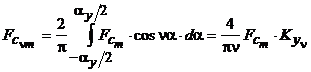где 
- коэффициент укорочения шага обмотки.
Если выбрать шаг секции равным 
, то гармоническая составляющая n порядка становится равной нулю:
Укорочение шага используют для подавления, главным образом, 5-й и 7-й гармоник, выбирая шаг 
. При этом первая гармоника уменьшается незначительно 
. Третья гармоника и кратные трем гармоники МДС не оказывают влияния на результирующее поле трехфазной обмотки (см. п. 3.3), поэтому никаких специальных мер для их подавления не применяют.
МДС катушечной группы
Вторым способом подавления высших гармоник МДС является распределение обмотки. В пределах полюсного деления каждая фаза распределенной обмотки содержит не одну, а q последовательно соединенных секций, образующих катушечную группу.
Рассмотрим катушечную группу из трех секций (
) с полным шагом (
). Результирующая МДС катушечной группы определяется суммой МДС секций 
, сдвинутых по отношению друг к другу на угол 
. Суммарная кривая (рис.3.12) имеет ступенчатый вид, приближаясь с увеличением q к синусоиде. Состав гармоник этой кривой можно определить, выполнив геометрическое суммирование соответствующих гармоник МДС секций. Первые гармоники можно представить в виде векторов, сдвинутых по отношению друг к другу на угол 
(рис.3.13). Многоугольник ABCD вписывается в окружность, поэтому результирующий вектор
,
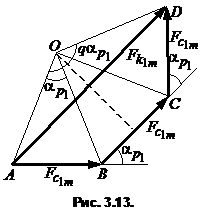
где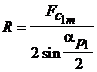 
- радиус окружности.
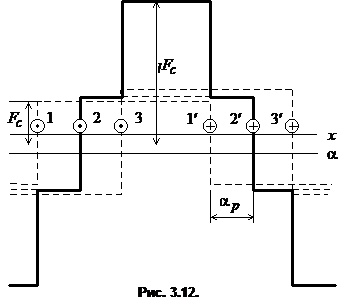
Выражение для первой гармоники результирующей МДС катушечной группы обычно записывают в виде
,
где 
- коэффициент распределения.
При определении n гармоники МДС катушечной группы необходимо учесть, что угол сдвига между векторами 
увеличивается в n раз: 
. Тогда
,
где 
.
Анализ этого выражения показывает, что с увеличением q амплитуда первой гармоники снижается незначительно (при 
), а амплитуды высших гармоник существенно уменьшаются, за исключением гармоник зубцового порядка:
,
где k - любое целое число. Коэффициент распределения зубцовых гармоник равен коэффициенту распределения первой гармоники,
.
Для уменьшения влияния зубцовых гармоник следует принимать 
. При этом порядок зубцовых гармоник оказывается достаточно велик (
), а следовательно, их амплитуда будет незначительна (
), и влиянием этих гармоник на результирующую кривую МДС катушечной группы можно пренебречь.
Если катушечная группа состоит из секций с укороченным шагом, то при определении результирующей МДС катушечной группы необходимо учесть коэффициент укорочения 
:
,
где 
- обмоточный коэффициент.
МДС одной фазы
Для двухслойной обмотки МДС фазы, приходящаяся на один полюс, равна удвоенной МДС катушечной группы, поэтому
.
Число витков секции 
связано с полным числом последовательно соединенных витков фазы W соотношением
.
Учитывая также, что ток фазы 
, преобразуем выражение для амплитуды МДС фазы к виду
.
Амплитуда 
определяет МДС n-й гармоники на магнитной оси фазы в момент времени, когда ток фазы имеет максимальное значение. Закон распределения МДС фазы во времени и пространстве определяется уравнением
.
На рис. 3.14 сплошной линией показана первая гармоническая МДС в момент времени 
,
а пунктиром показана эта МДС в произвольный момент времени
.
МДС трехфазной обмотки
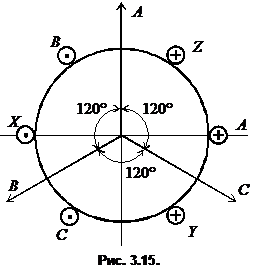
Пусть на статоре уложена симметричная трехфазная обмотка (рис. 3.15). Магнитные оси фаз сдвинуты в пространстве на 120°. Включим эту обмотку в сеть переменного тока, так чтобы по фазам протекали токи
;
;
.
Найдем результирующую МДС трехфазной обмотки, созданную этими токами. С целью облегчения задачи будем учитывать лишь первые гармоники фазных МДС
;
;
.
Преобразуем данные выражения, заменяя произведение косинусов двух углов на полусумму косинусов суммы и разности этих углов:
;
;
.
Отсюда получаем выражение для результирующей МДС трехфазной обмотки:
. (3.4)
Данное выражение представляет собой уравнение бегущей волны. Положение максимума волны определяется углом 
, зависящим от времени,
.
Следовательно, магнитная ось результирующего поля будет вращаться с угловой частотой 
. В связи с этим амплитуду результирующей МДС трехфазной обмотки часто изображают на пространственной комплексной плоскости в виде вращающегося вектора (рис. 3.16)
.
Важно отметить, что положение вектора 
совпадает с изображающим вектором тока обмотки статора
.
Это обстоятельство позволяет упростить анализ процессов и явлений в электрических машинах, рассматривая вместо взаимодействия МДС взаимодействие соответствующих токов.
Третьи гармоники фазных МДС
;
;
взаимно компенсируются в трехфазной обмотке, так как их амплитуды сдвинуты во времени на 
периода (на электрический угол 120°), а в пространстве совпадают по фазе.
Сделанный вывод справедлив для всех гармоник, кратных трем. Остальные высшие пространственные гармоники фазных МДС создают результирующие МДС малой амплитуды, поэтому ими часто пренебрегают.
Таким образом, трехфазная обмотка при питании ее симметричной трехфазной системой токов создает практически синусоидально распределенную МДС, вращающуюся с угловой частотой w.
В заключение отметим, что приведенный анализ справедлив как для двухполюсных, так и для многополюсных электрических машин. Необходимо лишь учесть, что в многополюсных машинах все углы уменьшаются в р раз,
.
Поэтому во столько же раз снижается и частота вращения результирующей МДС:
.
