Характеристика системы, используемой для измерительных целей, определяется в первую очередь шириной полосы частот В, временем нарастания, а т технике высокого напряжения еще и временем ответа t. Под временем нарастания импульса напряжения или тока [Л. 70, 77] понимают промежуток времени, в течение которого рассматриваемая величина возрастает от 10 до 90% своего конечного значения (рис. 22) при подаче на вход напряжения с бесконечно крутым фронтом; иначе говоря, эта характеристика определяется переходной функцией системы. Помимо приведенных выше, существуют еще и другие определения времени нарастания, например возрастание рассматриваемой не личины от 1 до 99% или от 30 до 90% конечного значения, однако они не получили широкого распространения. Следует еще упомянуть о длине фронта импульса по определению МЭК [Л. 78, 79].
![]()
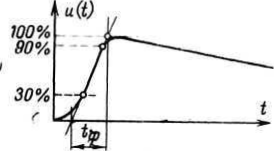
Рис. 23. Определение длины фронта импульса напряжения по МЭК.

Рис. 24. Два возможных определения постоянной времени переходной функции.
Последний термин широко применяется при испытаниях электрооборудования, но не для описания высокочастотных характеристик передачи, а лишь для фиксирования параметров стандартного импульса (рис. 23).
До введения понятия времени нарастания качество делителей напряжения обычно оценивали по их постоянным времени. Малые Постоянные времени обеспечивали высокие верхние предельные частоты. Между временем нарастания ta и постоянной времени Т экспоненты выходного сигнала существует жесткая зависимость. Если к входу RС-цели приложить импульс напряжения U1(t) = U0s(t) с бесконечно крутым фронтом, то напряжение на выходе возрастает по экспоненте (рис. 24). Время нарастания ta может быть вычислено из уравнения [Л. 77]
![]()
Постоянная времени переходной функции может быть определена графически, а также из интеграла

где S — площадь, заштрихованная на рис. 24.
Определение величины Т по касательной, проходящей через начало координат, теряет смысл, когда процесс носит колебательный характер. Большие размеры установок, применяемых в ТВН, обусловливают заметные индуктивности подводящих проводов и паразитные емкости.
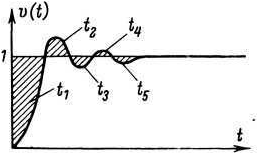
Рис. 25. Определение времени ответа.
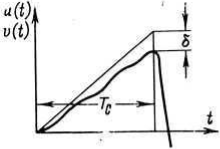
Рис. 26. Погрешность измерения амплитуды (δ) при воспроизведении косоугольных волн.
Поэтому часто на экспоненциальное изменение напряжения накладываются более или менее выраженные колебания. Чтобы и в этом случае можно было определить постоянную времени, введено понятие времени ответа (рис. 25) [Л. 79, 80]. Это время представляет собой площадь, заключенную между кривой переходной функции v(t) = w(t)k, прямой параллельной оси абсцисс и соответствующей конечному значению (1) и осью ординат:
![]()
Время ответа служит для расчета амплитудных погрешностей при измерении косоугольных волн. На рис. 20 показано воспроизведение косоугольной волны напряжения u(t) при помощи делителя напряжения с временем ответа ίtп. Относительная амплитудная погрешность зависимости от времени среза Тс может быть определена из следующего выражения:
Это уравнение справедливо только тогда, когда напряжение возрастает линейно и измерительное устройство имеет экспоненциальную характеристику воспроизведения, а также и при колебательном характере переходной функции, если время среза больше времени достижения стационарного режима. На практике импульс нс вполне косоуголен и на начальном участке изменение имеет очень малую крутизну, поэтому колебания, накладывающиеся на измеряемый сигнал, невелики. Поэтому данное уравнение справедливо даже и тогда, когда время среза меньше времени установления стационарного значения у переходной функции.
Определение времени ответа теряет смысл, когда переходная функция сильно колеблется (чрезмерное время установления стационарного значения) или система имеет большое время запаздывания (это время у делителей высокого напряжения, которые рассчитываются на малое время нарастания, всегда известно). По результатам определения времени ответа можно судить о характеристике передачи только тогда, конца известна одновременно сама переходная функция или по крайней мере ее «выброс» за стационарное значение (выброс характеризуется отношением А/В) (рис. 27). Действительно, площади можно сделать одинаковыми путем соответствующей подгонки компенсированного омического или демпфированного емкостного делителя напряжения. Не составляет труда также сделать t2>t1. что соответствует даже отрицательному времени ответа. Отсюда следует, что значение времени ответа само по себе не может служить надежным критерием качества делителя напряжения. Следует еще добавить, что на значение времени ответа можно существенно влиять, изменяя время задержки у подводящих проводов.
Однозначно характеризует делитель напряжения время нарастания Определение времени нарастания имеет смысл при выбросе за стационарное значение максимум на 5%. Так как делители напряжения с выбросом более 5% в качестве измерительного устройства применяются довольно редко, предпочитают вместо значения времени ответа tп пользоваться значением времени нарастания ta [Л. 70].
Время нарастания дает экспериментатору ясное представление о применимости делителя напряжения для измерений. Оно позволяет довольно просто производить оценку сглаживания фронта импульса, а также времен нарастания у делителей и электроннолучевых осциллографов. Времена нарастания систем из независимых элементов могут быть определены путем геометрического сложения [Л. 18, 77, 81]:![]()
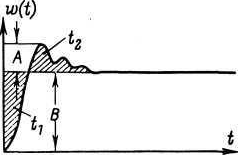
Рис. 27. Определение выброса за стационарное значение.
Можно определить действительное время нарастания выходного сигнала при воздействии прямоугольного импульса по времени нарастания, наблюдаемого на экране электроннолучевого осциллографа, из уравнения
![]()
В этом уравнении: ta — действительное время нарастания сигнала; tac—наблюдаемое по экрану время; ta0 — собственное время нарастания электроннолучевого осциллографа. Точность этого расчета сильно снижается, если время нарастания сигнала меньше собственного времени нарастания электроннолучевого осциллографа. Так, например, при ta0/ta=3 и точности отсчета значений tac=5% различие между действительным и рассчитанным ta может составлять 100%.
Геометрическое сложение, строго говоря, справедливо только для системы Гаусса с выбросом за стационарное значение менее 5% (оно, например, недопустимо при передаче импульсов с крутым фронтом по коаксиальному кабелю, в котором проявляется поверхностный эффект). Под системой Гаусса здесь подразумеваются передающие элементы, затухание которых у верхнего предела частот может быть описано кривой Гаусса, т. е. оно увеличивается пропорционально квадрату частоты (например, как показано на рис. 28, с 30 до 60 МГц затухание возрастает с —3 до —12 дБ). Для большинства цепных схем затухание можно с достаточной точностью аппроксимировать при помощи функции Гаусса.
Приведенное выше уравнение для геометрического сложения времен нарастания вытекает из основной предельной теоремы вероятности [Л. 77, 82]. На этом же базируется и математическая связь между временем нарастания и шириной полосы частот с нормированным затуханием, например 3 дБ. Для фильтра нижних частот с хорошей характеристикой передачи импульсов переходная функция в кратчайший промежуток времени достигает конечного значения без заметного выброса (система Гаусса) и время нарастания можно вычислить по ширине полосы [Л. 81]
![]()
Это уравнение пригодно не для всех широкополосных измерительных усилителей, а только для широкополосных импульсных усилителей, передаточная функция которых имеет гауссово падение.

