Автоматическое управление газотурбинной установкой осуществляется в двух совершенно разных режимах. Первый режим —это пуск и остановка газотурбинного агрегата. Второй режим — стабилизация скорости вращения вала ТНД при изменяющейся нагрузке. Два этих режима обеспечиваются двумя разными подсистемами — подсистемой пуска и блокировок и подсистемой регулирования. В некоторые моменты обе эти подсистемы работают одновременно, будучи связанными через регулирующий клапан. Автоматическое управление в двух режимах имеет два аспекта: математический и прикладной (инженерный).
Дадим математическую постановку задачи для режима пуска. Математическое описание газотурбинной установки — основного тракта преобразования энергии — имеет вид
(1.5)
где x — вектор, имеющий составляющее x1, х2, хп, под которыми можно понимать: x1=Θ1 — температура рабочего тела перед ТВД, х2=ωв и х3=ώн — угловая скорость вращения соответственно ТВД и ТНД, x4=P1 — давление рабочего тела перед ТВД, х5=рн — давление газа после нагнетателя, х6=Gн — расход газа через нагнетатель и т. д.; u=т — скалярное управляющее воздействие, т. е. положение т регулирующего клапана; f(x, u) — вектор-функция с координатами f, которыми характеризуются законы преобразования энергии и течения рабочего тела по проточной части.
На составляющие вектора наложены ограничения
предохраняющие турбину от аварийных режимов.
Запишем несколько ограничений, учитывая, что координаты не могут принимать отрицательных значений:
и т. д. Ограничения могут накладываться не только на сами координаты, но и на скорости их изменения. Так, во время пуска должна быть ограничена скорость нарастания температуры перед ТВД, т. е.
Пусть в пространстве состояний дано начальное значение вектора х в момент t0, т. е. х (t0), и конечное состояние этого вектора в момент t1, т. е. х (t1). Требуется с помощью управления и (ί) перевести вектор х из начального состояния х (t0) в конечное х (t1). К движению между точками х (t0) и х (t1) могут предъявляться определенные требования, поэтому данная общая задача распадается на две частные.
- Найти такое управление и (t), чтобы время перевода t1 — t0 было минимальным при выполнении всех ограничений.
- Найти такое управление и (t), чтобы за данное время движения t1—t0=τ расход топлива был минимальным при соблюдении всех ограничений.
При условиях 1 и 2 задача пуска газовой турбины пока не решена. Дело в том, что уравнение (1.5), записанное в общей математической форме, нельзя конкретизировать для нестационарных термодинамических процессов. Формулы (1.1) — (1.4) справедливы только для стационарных процессов. Всё процессы в турбине при ее пуске нестационарны, а для них нет приемлемого математического описания. Естественно, что со временем задача математического описания нестационарных термодинамических процессов будет решена и, следовательно, оптимизированы пусковые режимы. Но даже если иметь строгое решение задачи, то реализовать полученный закон управления не всегда возможно по двум причинам: не все координаты в процессе работы турбины наблюдаемы, из-за сложности применяемых элементов может снизиться надежность системы управления.
Остановимся подробнее на этих причинах. Многие параметры, характеризующие работу турбины, контролируются; перечень их дан ниже. Но есть весьма важные параметры, которые пока не контролируются. К ним можно отнести температуру лопаточного аппарата, перепад температур по диску рабочего колеса, зазор между лопатками и корпусом и т. д. Перечисленные параметры весьма существенны при пуске, который, вообще говоря, должен происходить так, чтобы не превышать допустимых ограничений на них. Следовательно, данные параметры должны контролироваться, но пока это невозможно из-за отсутствия измерительных приборов. Делаются попытки замерить эти параметры косвенным путем, но пока они не увенчались успехом.
Законы управления, соответствующие указанным выше критериям, достаточно сложны, и для их реализации необходимо применение элементов аналоговой или цифровой техники. Вычисления часто содержат такие операции, как извлечение корня, возведение в степень, деление, умножение, суммирование и т. д. Все эти операции должны выполняться непрерывно в процессе пуска в реальном масштабе времени. Оптимальное управление можно рассчитать заранее на цифровой машине и иметь его в виде программы. Реализация сложной программы также часто требует элементов аналоговой вычислительной техники или специальных маломощных следящих систем. Кроме того, программу следует корректировать при изменении условий пуска. Введение в систему управления элементов вычислительной техники, специальных следящих систем и других сложных аппаратов, необходимых для реализации оптимальных законов, неизбежно снизит ее надежность.
Конкурентом строго математического решения задачи об оптимальном управлении пуском выступает конкретный инженерный опыт и способность человека к весьма точной экстраполяции. Действительно, конструируя газовую турбину, инженер хорошо знает все ее свойства и возможности управления, которые впоследствии проверяются во время экспериментов над отдельными узлами и при стендовых испытаниях машин. Поэтому опыт позволяет находить, может быть, не оптимальные, но во всяком случае близкие к оптимальным законы управления, которые, как правило, легче реализуются и вполне удовлетворяют практику. Законы управления пуском, реализации которых посвящена гл. IV, найдены опытным путем.
Обратимся теперь к стабилизации рабочих режимов при изменении нагрузки, в частности к стабилизации скорости вращения ТНД. Здесь дело обстоит совсем иначе, чем при пуске, т. е. задача стабилизации может иметь строгое решение, которое достаточнопросто реализуется практически. Перейдем к постановке задачи стабилизации рабочих режимов с математической и практической точек зрения.
Уравнение движения замкнутой системы стабилизации записывается в той же векторной форме, что и уравнение (1.5), хотя координаты вектора могут иметь другие значения:
В такой форме задача устойчивости системы не решена, можно говорить об устойчивости только частных решений. Но так как изменение координат, по самому смыслу работы системы стабилизации, происходит в малой окрестности рабочей точки, т. е. заданного рабочего режима, то к уравнению (1.5) можно применить принцип линеаризации и заменить нелинейную задачу линейной. Тогда математическое описание системы регулирования можно представить уже в виде линейного векторного уравнения
(1.6)
где А и В — матрицы с постоянными элементами.
Конкретная расшифровка векторно-матричного уравнения (1.6) дана в гл. V. Задача устойчивости и качества системы, которая имеет математическое описание (1.6), хорошо разработана и доведена до инженерных рекомендаций. Но здесь опять сталкиваемся с некоторыми трудностями при расчете систем стабилизации, имеющих высокий порядок, а именно к таким системам относится газовая турбина. Поэтому, как правило, математическое описание, даже линейное, стараются еще больше упростить, понижая порядок системы дифференциальных уравнений. Все упрощения, конечно, нуждаются в достаточном инженерном обосновании.
Дополнительные трудности возникают, когда задана некоторая область режимов стабилизации, которые приходится рассчитывать уже для нескольких рабочих точек. Следовательно, математически расчет режимов стабилизации сводится к исследованию нескольких идентичных систем линейных дифференциальных уравнений с постоянными коэффициентами. Как указывалось, решение данной задачи доведено до инженерных приемов и рекомендаций.
С инженерной, практической, точки зрения решение задачи стабилизации облегчается тем, что все промышленные и специально созданные регуляторы имеют широкий диапазон настроек параметров. Поэтому упрощения математического описания турбины, приводящие к отклонению реальных процессов от расчетных, легко учитываются при настройке 'регуляторов. С математической точки зрения необходимо определить погрешности решений при замене нелинейной системы линейной. Практически этого не делают, так как наличие различных настроек в регуляторах позволяет компенсировать погрешности. Качество системы стабилизации определяется моделированием при проектировании и проверяется при натурных испытаниях машин.
Проиллюстрируем все сказанное выше графически на примере управления температурой перед ТВД, т. е. температурой камеры сгорания. В процессе пуска ограничивается скорость нарастания температуры перед ТВД из условия допустимых термических и механических напряжений на лопатках и диске рабочего колеса. Ограничивается и сама температура также из условий надежности работы лопаточного аппарата. Возьмем пространство состояний, образованное координатами
(рис. 1.9). Проведем линии ограничений
Получим замкнутую область ABCD, за пределы которой координаты и Θ не могут выходить. Но траектории изменения этих координат могут находиться на границе области, т. е. на линиях ВС и CD. Зададим в пространстве состояний при t0=0 начальное значение температуры камеры сгорания
(точка 1 на рис. 1.9, а), при — конечное
(точка 2).
Следует найти такое управление и (t), т. е. закон изменения положения регулирующего клапана, чтобы точки 1 и 2 соединились некоторой траекторией, не выходящей за пределы замкнутой области.
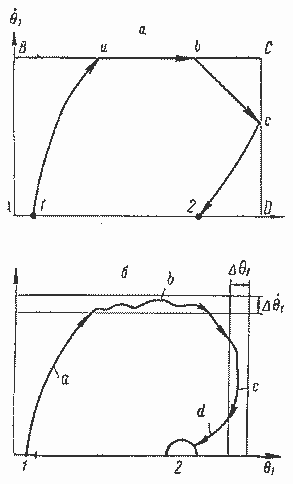
Рис. 1.9. .Управление температурой и скоростью ее изменения перед турбиной высокого давления.
Примером может служить траектория 1, а, b, с, 2. Следующая задача заключается в стабилизации температуры в точке 2. Строгое математическое решение управления пуском показано на рис. 1.9, а.
Рассмотрим теперь решение управлением параметрами
в инженерном плане. Возьмем пространство состояний (см. рис. 1.9, б). В отличие от предыдущей задачи, начальное и конечное состояния задаются не точками, а соответственно отрезком 1 и областью 2. Ограничения задаются не линиями, а некоторыми областями
Траектория, соответствующая этим ограничениям, показана линией а, b, с, d. Ценным свойством данной траектории является то, что в полосах ΔΘΧ и ΔΘ1 движение может быть любым, лишь бы оно не выходило из этих полос. Так как на движение внутри полос не накладывается ограничений, то реализация его значительно упрощается. Стабилизацию температуры теперь следует проводить не в точке, а в некоторой области. Движение координат в области также может быть любым. Это значительно облегчает задачу стабилизации.
Отметим еще одно отличие технического решения задачи от математического. Математическое решение не допускает выхода траектории за область ограничений. В технических системах такой выход возможен в аварийных ситуациях. Поэтому техническая система должна предусматривать устройства, вступающие в действие после нарушения ограничений. Обычно выход координат газовой турбины за область ограничений влечет за собой ее аварийную остановку. В аварийном режиме системы управления и стабилизации работают в режимах быстрых отсечек (например, быстрое закрытие регулирующего клапана и быстрый сброс рабочего тела, имеющего большую энергию, путем открытия сбросных клапанов).
Турбина имеет не одну координату управления, а несколько. Поэтому области и процессы рассматриваются не на плоскости, а в многомерном пространстве. Но существо вопроса от этого не меняется. Следовательно, выбрав разумные области ограничений и стабилизации, можно создать качественные и достаточно простые системы управления. Выбор областей ограничений — задача не такая простая, как кажется на первый взгляд. Она зависит от целого ряда взаимосвязанных факторов.
Нами было рассмотрено управление основным процессом преобразования энергии в турбине. Но управлять следует и вспомогательными механизмами. Управление ими значительно проще и сводится к их включению или выключению в определенной последовательности, которая может быть задана в программно-временной или пооперационной форме (последующая операция выполняется после совокупности предыдущих). Могут быть применены и комбинированные способы управления.
Из приведенных рассуждений, очевидно, ясна цель автоматического управления: осуществлять перевод ГТУ из одного режима на другой без нарушения ограничений, накладываемых на координаты; стабилизировать параметры в окрестностях заданных режимов; строго соблюдать последовательность операций при пусках и остановках; предотвращать развитие аварийных режимов; непрерывно или дискретно контролировать работу наиболее ответственных узлов и сигнализировать об отклонениях от их нормальных режимов.
