В области теоретического и экспериментального исследования нерегулируемых эжекторов в СССР и за рубежом проделана большая работа. Однако среди существующих методик расчета нет простой, отражающей все процессы протекающей жидкости (например, явление смешивания потоков, кавитации потока и прочее). Кроме того, теоретические обоснования нередко не подтверждаются опытом в широком диапазоне типоразмеров эжекторов. Поэтому результаты расчетов эжекторов по разным методикам значительно отличаются друг от друга.
Предлагаемая методика расчета нерегулируемых эжекторов построена на основе методики Е. Я. Соколова [13], в нее внесены дополнения и уточнения, полученные на основе экспериментальных исследований натурных нерегулируемых эжекторов в широком диапазоне типоразмеров, проведенных на Братской гидроэлектростанции.
Уравнение гидравлической характеристики водоструйных насосов по Е. А. Соколову [ 13], выведенное на основе закона импульсов применительно к неупругим средам, с введением дополнительного опытного коэффициента неравномерности имеет вид
(8)
(9)
(10)
— относительный напорный коэффициент, характеризующий относительное соотношение эксплуатационных напоров; условно делят эжекторы в зависимости от напоров на средненапорные (h ~ 0,2-0,25), высоконапорные (λ >0,25) и низконапорные (h < 0,2); q — относительный расходный коэффициент, характеризующий массу всасываемого потока, приходящуюся на единицу массы рабочего потока, и являющийся одним из показателей эффективности эжектора, определяется по формуле
(11) к — относительный геометрический коэффициент, характеризующий отношение площадей проходных сечений всасываемого и рабочего потоков:
(12) φ1= 0,950; φ2 = 0,975; φ3 = 0,900; = 0,925 — скоростные коэффициенты сопла, камеры смешивания, диффузора и входного участка в камеру смешивания соответственно, полученные Е. Я. Соколовым экспериментальным путем;
— давление рабочего
и всасываемого потоков в срезе сопла и смешанного потока в конце камеры смешивания; fр. с. с., f Вc. c. c.- площади проходных сечений рабочего и всасываемого потоков в срезе сопла (или, что то же самое, в начале камеры смешивания). Следует добавить, что это уравнение гидравлической характеристики эжектора выведено при следующих допущениях: рабочая и всасываемая жидкости несжимаемы, температура рабочей и всасываемой сред одинакова, расстояние от выходного сечения сопла до входа в камеру смешивания равно нулю, толщина стенки сопла на выходе равна нулю.
После дальнейших преобразований уравнение гидравлической характеристики водоструйного эжектора принимает вид, удобный для расчетов:
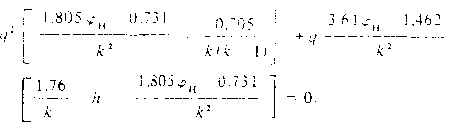(13)
В уравнении (13) опытный коэффициент неравномерности характеризует степень смешивания рабочего и всасываемого потоков, т. е. степень выравненности скорости в поперечном сечении камеры смешивания. Значения коэффициента φ в расчетном режиме близки к единице, что показывает зависимость φн =f(h), представленная на рис. 12, а.
Зависимость для определения оптимального отношения площадей сечений камеры смешивания и сопла по заданному значению относительного напорного коэффициента, после подстановки скоростных коэффициентов и коэффициента приведения кг (рис. 12, б) принимает вид
(14) где кг — геометрический коэффициент приведения, равный отношению опытного геометрического коэффициента к расчетному.
Явление кавитации в эжекторах связано с понижением давления жидкости в начальном участке зоны смешивания при определенной температуре до давления ее насыщенных паров. При этом начинается интенсивный процесс парообразования, т. е. выделения растворенного в жидкости воздуха, срыв струй от поверхности камеры смешивания, переход паров жидкости в область более высокого давления; конденсация с образованием местных зон повышенного давления, сопровождающаяся шумом, ударами в корпус камеры смешивания.
Кавитация начинается в местах соприкосновения рабочей и всасываемой струй, т. е. в месте наибольшей турбулизации потоков. Еще задолго до возникновения кавитации в большей части сечения струи отдельные ее очаги появляются в зонах локальных пульсаций скорости. Однако внезапный срыв работы эжектора происходит, когда кавитационными явлениями будет охвачен не только начальный участок зоны смешивания, но и вся толща струи всасываемой жидкости. Па начальную и конечную стадии кавитации влияет содержание воздуха в жидкости, ее температура, и чем выше температура, тем выше давление, при котором наступает кавитация), давление перед эжектором, сопротивление трубопроводной трассы всасываемого потока, степень турбулизации в зоне смешивания, скорость всасываемого потока непосредственно перед входом в камеру смешивания, т. е. расход всасываемого потока и относительный расходный коэффициент, который и является, в первую очередь, показателем наступления кавитационного режима, при котором поглощается энергия струи рабочего потока.
Оценку кавитационного режима работы эжектора рекомендуется также производить по формуле Е. Я. Соколова, которая после подстановки скоростных коэффициентов и опытного коэффициента приведения (см. рис. 12,в) принимает вид
(15)
где qKB - кавитационный коэффициент расхода (соответствующий началу кавитации); kкв - кавитационный коэффициент приведения, равный отношению опытного кавитационного коэффициента расхода к расчетному; Hв - избыточный напор насыщенного пара (вакуум) при температуре рабочей среды.
Порядок расчета. При расчете водоструйных эжекторов (в последующем для простоты будем именовать просто эжекторами) системы технического водоснабжения заданными величинами являются:
Эксплуатационные напоры Нр и Нвс, т. е. отметки верхнего и нижнего бьефов гидроэлектростанции, отметка оси месторасположения эжектора и зависимость потерь напора от расхода в подводящих трубопроводах рабочего и всасываемого потоков;
Характеристика потребителя системы технического водоснабжения гидроэлектростанции — зависимость расхода от потерь напора на выходе из эжектора или от гидравлического сопротивления всей выходной трубопроводной трассы эжектора.
Потребная производительность эжектора, т. е. для эжектора второго типа расход на выходе, определяется специальным тепловым расчетом или анализом уже эксплуатируемых систем заводом-изготовителем основного оборудования (см. гл. 1) и уточняется во время работы гидроэлектростанции.
Расчет геометрических параметров нерегулируемого эжектора: диаметра сопла dс и диаметра камеры смешивания DK. см и эксплуатационных характеристик эжектора производится в следующей последовательности:
- Определяются гидравлические потери в подводящих трубопроводах рабочего, всасываемого и выходного потоков и напоров.
- Определяется относительный напорный коэффициент h по формуле (10).
- Определяется оптимальный геометрический коэффициент к по формуле (14).
Необходимо иметь в виду, что если уровни воды в бьефах гидроэлектростанции в процессе эксплуатации меняются в незначительных пределах, то можно спроектировать нерегулируемый эжектор с оптимальными геометрическими размерами и оптимальный геометрический коэффициент к будет определяться по формуле (14).
При значительных колебаниях уровней верхнего и нижнего бьефов спроектировать эжектор с оптимальными геометрическими размерами не удается. В этом случае относительный геометрический коэффициент выбирается из условия обеспечения стабильности работы эжектора (без кавитации и ’’опрокидывания”, т. е. когда (Qвс = 0) во всем диапазоне изменения уровней верхнего и нижнего бьефов в три этапа:
а) определение геометрического коэффициента кх, соответствующего началу ’’опрокидывания”, т. е. началу гидравлического процесса, когда QBC = 0, q= 0, Qp = QBых. Это условие выполняется при подстановке в уравнение (13) значения q = 0 и h = hmax, и при решении уравнения
(16)
б) определение геометрического коэффициента к2, соответствующего началу кавитации, т. е. срыву работы эжектора. Это условие выполняется, если приравнять относительный расходный коэффициент q из уравнения (13) расходному кавитационному коэффициенту qКВ, определенному по формуле (15). Значение кг находится подбором, путем подстановки в уравнения (13), (15) значения (для указанных напорных параметров) .
в) рассмотрение возможности проектирования эжектора на заданные напорные параметры, определяемой неравенством к1>к>к2, где к — искомый расчетный геометрический коэффициент, обеспечивающий бесперебойную работу эжектора в заданном диапазоне изменения уровней верхнего и нижнего бьефов.
При невыполнении неравенства для всего диапазона изменения h при заданных напорных параметрах спроектировать один эжектор невозможно. При выполнении неравенства искомый расчетный геометрический коэффициент проектируемого эжектора должен быть выбран в интервале значении кх и кг, однако по возможности ближе к значению к2.
- Определяется оптимальный относительный расходный коэффициент q по уравнению (13).
- Определяются расходы рабочего и всасываемого потоков:
(17)
- Определяется относительный кавитационный коэффициент по формуле (15). Условием отсутствия кавитации является выполнение неравенства q < qКВ. Если q > qKB, необходимо увеличить коэффициент к.
- Определяется скорость рабочего потока по формуле
(18) где φ=0,95 — скоростной коэффициент сопла (рабочего потока), g= 9,81 м/с2 - ускорение силы тяжести.
- Определяется площадь поперечного сечения и диаметр сопла dc :
(19)
(20)
- Определяется диаметр камеры смешивания DK. см, по формуле (12)
- Составляется уравнение гидравлической характеристики эжектора в форме q=f(h), анализируется работоспособность эжектора при всех колебаниях верхнего и нижнего бьефов гидроэлектростанции.
- Определяется коэффициент полезного действия эжектора. Известно, что коэффициент полезного действия (КПД) — безразмерная величина, характеризующая степень совершенства технического устройства в отношении осуществления в нем процессов передачи энергии или преобразования ее из одной формы в другую. Определяется КПД отношением полезной энергии к суммарной затраченной.
Для эжекторов первого типа, служащих для откачки воды, КПД определяется по известной формуле, в которой полезная энергия оценивается расходом только всасываемого потока:
(21)
Приведенное выражение КПД не является универсальным для эжекторов любого назначения.
Очевидно, что для эжекторов второго типа, служащих для нагнетания жидкости к заданному объекту, например, работающих в системе ТВС, под КПД следует понимать отношение энергии воды, использованной в системе охлаждения потребителя, к энергии, затраченной рабочим потоком, поступающим из верхнего бьефа. В этом случае в выражение использованной энергии входит энергия как всасываемого, так и рабочего потока. КПД самотечной и насосной установок, аналогичных по своему назначению эжекторной, определяются соответственно по формулам :
где Э — электроэнергия, затраченная двигателем насоса. Поэтому для определения КПД эжекторов второго типа целесообразно использовать следующее выражение:
(22)
По значению η1 оценивается оптимальность спроектированного эжектора первого типа для заданных напорных условий и сравниваются друг с другом эжекторы первого типа. По значению η2, кроме перечисленного выше применительно к эжекторам второго типа, сравниваются эжекторные установки с установками самотечными и насосными. Максимальное значение р2 значительно выше, чем η1. Так, при натурных испытаниях эжекторов на Братской ГЭС получены следующие значения КПД для эжекторов оптимальной геометрии средненапорного типа: η1≈35%, η2≈ 60%.
